
- •Лекційно-практичний курс
- •З математичного аналізу.
- •Частина 1. Вступ до аналізу.
- •Передмова
- •Елементи теорії множин. Лекція №1 Відношення. Функції.
- •1. Множини, дії над множинами, добуток.
- •2. Відношення. Функції. Приклади.
- •3. Образ, прообраз. Композиція
- •Практичне заняття № 1
- •Довести
- •Лекція №2. Відношення порядку. Множина дійсних чисел. Точна верхня (нижня) границя.
- •1. Відношення порядку. Верхня границя. Приклади.
- •2. Зростаючі функції.
- •3. Дійсні числа. Теорема про точну верхню границю.
- •Практичне заняття № 2 Тема: Відношення, функції. Дії над функціями
- •Лекція №3. Властивості дійсних чисел. Принцип Архімеда.
- •1. Класи чисел
- •2. Принцип Архімеда. Наслідки.
- •Практичне заняття №3 Тема: Відношення порядку. Впорядковані множини. Точна верхня і точна нижня грані. Дійсні числа.
- •Практичне заняття № 4 Тема: Верхня та нижня грані множини. Точна нижня та верхня грані.
- •Практичне заняття №5 Тема: Дійсні числа. Формули скороченого множення. Основні нерівності.
- •Практичне заняття №6 Тема: Принцип математичної індукції.
- •Лекція №4. Кардинальні числа.
- •1. Означення кардинального числа (потужності множини).
- •2. Теорема про множину як завгодно великої потужності.
- •3. Зчисленні множини.
- •Лекція №5. Множини потужності континуум, та їх властивості.
- •1. Потужність континуума.
- •2. Властивості потужності континуум.
- •Практичне заняття № 7 Тема: Еквівалентні множини. Зчислені множини. Множини потужності континуум.
- •Елементи топології. Лекція №6. Метричні, нормовані простори. Відкриті, замкнені множини.
- •1. Метричні простори. Приклади. Шар. Сфера.
- •3. Відкриті, замкнені множини. Замикання.
- •Лекція №7. Неперервні функції. Гомеоморфізми.
- •1. Означення неперервної функції та її властивості
- •2. Гомеоморфізми.
- •Лекція №8. Топологічні простори. Еквівалентні метрики і топології.
- •1. Еквівалентні метрики і норми,
- •2. Топологічні простори.
- •Практичне заняття № 8 Тема: Елементи топології
- •Послідовності. Лекція №9. Границя послідовності та її властивості
- •Лекція №10 Послідовності в r1 та в Rn
- •1. Властивості пов’язані з діями над послідовностями дійсних чисел.
- •2. Теорема Вєйєрштрасса про монотонну послідовність. Число е.
- •3. Лема про три границі. Граничні переходи у нерівностях.
- •4. Топологічні добутки. Послідовності в Rn.
- •Практичне заняття №9 Тема: Границя послідовності.
- •Практичне заняття №10 Тема: Обчислення границі послідовності. Число е.
- •Лекція №11 Границя функції. Означення по Коші і Гейне. Чудові границі.
- •1. Границя функції. Означення по Гейне і Коші.
- •2. Чудові границі:
- •Практичне заняття №11 Тема: Границя функції
- •Практичне заняття №12 Тема: 1а, 2а чудові границі.
- •Практичне заняття №13 Тема: Неперервні функції. Точки розриву функції та їх класифікація.
- •Компактні та зв’язні простори. Властивості неперервних функцій на компактних та зв’язних просторах. Лекція № 13 Компактні простори. Компактні множини в r1 і Rn
- •1. Означення компактних просторів. Приклади.
- •2. Властивості і ознаки компактності.
- •3. Теорема Больцано-Вєйерштрасса.
- •Практичне заняття №14 Тема: Компактні простори
- •Лекція № 14 Властивості неперервних функцій на компактних просторах.
- •1. Теореми Вєйерштрасса. Їх трактування в r1 і Rn.
- •2. Рівномірна неперервність. Теорема Кантора.
- •Лекція № 15 Зв'язні простори. Теорема Больцано-Коші в r1. Існування і неперервність оберненої функції для строго монотонної неперервної функції.
- •1. Означення. Неперервні відображення зв'язаних просторів.
- •2. Теорема про обернену функцію
- •Практичне заняття № 15 Тема: Зв’язні множини. Властивості функцій неперервних на відрізку. Рівномірна неперервність.
- •Лекція № 16 Означення та неперервність елементарних функцій.
- •1. Степенева функція.
- •2. Показникова функція.
- •3. Логарифмічна функція.
- •2. Ознаки Коші для границі послідовності і функції в r1. Повнота r1, Rn.
- •Практичне заняття № 16 Тема: Повні простори. Ознака Коші. Теорема про нерухому точку.
- •Завдання для самостійної роботи
- •Лекція №18. Початкові відомості про ряди. Числові ряди.
- •1. Додатні ряди.
- •2. Знакозмінні ряди.
- •3. Абсолютно збіжні ряди.
- •Практичне заняття № 17 Тема: Числові ряди, їх збіжність.
- •Література
2. Теорема Вєйєрштрасса про монотонну послідовність. Число е.
Теорема. Для того, щоб монотонно зростаюча (спадна) числова послідовність мала скінчену границю необхідно і достатньо, щоб вона була обмежена зверху (знизу).
Доведення.
Необхідність. Слідує з властивостей послідовностей, що збігаються.
Достатність. Нехай
зростаюча числова послідовність обмежена
зверху, тоді існує
![]() .
З означення
.
З означення![]() виконується властивості:
виконується властивості:
1.
![]() .
.
2.
![]()
Отже:
![]() ,
тобто виконується означення границі
послідовності і
,
тобто виконується означення границі
послідовності і![]() .
Аналогічно доводиться випадок спадаючої
числової послідовності.
.
Аналогічно доводиться випадок спадаючої
числової послідовності.
Приклад. Число е.
Покажемо, що існує
![]()
Розглянемо
послідовність
![]() Покажемо, що вона – спадна:
Покажемо, що вона – спадна:

(Нерівність
![]() випливає з нерівності Бернуллі)
випливає з нерівності Бернуллі)
За теоремою
Вєйєрштрасса існує скінчена границя
послідовності
![]() .
Тоді
.
Тоді![]() - існує. Позначимо
- існує. Позначимо![]()
3. Лема про три границі. Граничні переходи у нерівностях.
Теорема.
Нехай
 і
і - збіжні
числові послідовності з границями А
і В
відповідно.
- збіжні
числові послідовності з границями А
і В
відповідно.
Якщо А<В,
то
![]() .
.
Hexaй числові послідовності
 ,
, ,
, такі, що
такі, що .
Якщо
.
Якщо
 ,
, мають одну границю
мають одну границю ,
то
,
то збігається і має цю ж границю.
збігається і має цю ж границю.
Доведення. 2)
![]()
![]()
Нехай
![]() ,
тоді
,
тоді![]()
Отже,
![]() тобто
тобто![]() – границя послідовності{
– границя послідовності{![]() n}.
n}.
Наслідки
Нехай
![]() і
і![]() - числові
послідовності і
- числові
послідовності і
![]() =А
=А![]()
1. Якщо
![]()
![]()
2. Якщо
![]()
![]()
3. Якщо
![]()
![]()
4. Якщо
![]()
![]()
Приклад. Довести
![]()
Доведення.
 .
.
За лемою про три
границі
![]()
4. Топологічні добутки. Послідовності в Rn.
Повернемося до послідовностей у загальному вигляді.
Розглянемо ситуацію у метричних просторах, хоча усе зазначене нижче справедливе і у випадку довільних топологічних просторів.
Нехай
![]() -
метрики вЕ1
і Е2.
На множині Е1
-
метрики вЕ1
і Е2.
На множині Е1![]() Е2
за допомогою
формули
Е2
за допомогою
формули
![]() можна ввести метрику.
можна ввести метрику.
Приклад.
На
![]() маємо:
маємо:![]()
На
![]() маємо:
маємо:![]()
Теорема.
Для того, щоб послідовність (![]() 1,
1,
![]() 1),...(
1),...(
![]() n,
n,
![]() n),...
з Е1
n),...
з Е1![]() Е2
була збіжною в точці (
Е2
була збіжною в точці (![]() ,
b)у просторі
Е1
,
b)у просторі
Е1![]() Е2
необхідно і
достатньо, щоб послідовність
Е2
необхідно і
достатньо, щоб послідовність
![]() була збіжною вЕ1
до
була збіжною вЕ1
до
![]() ,a
,a
![]() була збіжною уЕ2
до b.
була збіжною уЕ2
до b.
Доведення.
Необхідність. Використовуючи
нерівність
![]() ,
а також збіжність (
,
а також збіжність (![]() n,
n,![]() n)
до (
n)
до (![]() ,
b)
,
b)![]() (згідно з означенням границі).
(згідно з означенням границі).
Достатність
випливає із збіжності
![]()
![]() і нерівності
і нерівності
![]()
Зауваження.
Теорема справедлива для добутку n
метричних просторів
![]() .
.
Приклад.
Якщо
![]() з природною метрикою, то за даною теоремою
маємо, що послідовність
з природною метрикою, то за даною теоремою
маємо, що послідовність![]() збігається до точки (
збігається до точки (![]() 1,…,
1,…,
![]() n)
тоді і тільки тоді, коли
n)
тоді і тільки тоді, коли
![]() в
в![]() .
.
Практичне заняття №9 Тема: Границя послідовності.
Необхідні відомості:
Визначення границі послідовності.
Властивості границь послідовностей.
Граничні переходи в нерівностях.
Властивості монотонних послідовностей.
Задачі:
Довести
 ;
;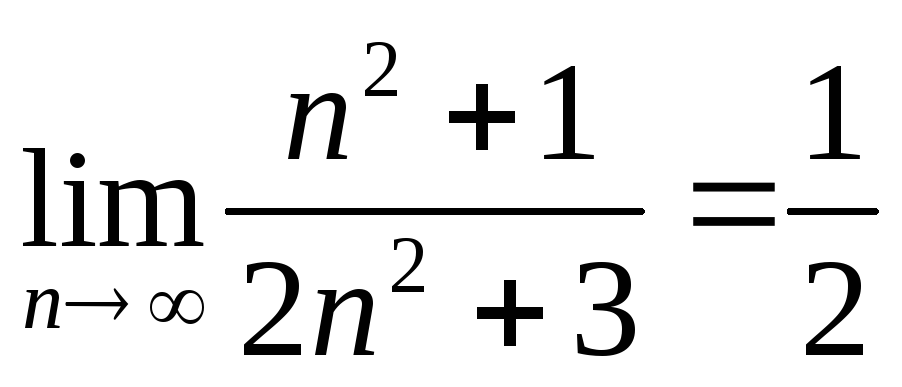 ;
;
Довести, що послідовність
 розбігається
розбігається
Довести збіжність послідовностей

 (використовувати критерій Коші).
(використовувати критерій Коші).
Використовуючи властивості граничних переходів розв’язати наступні задачі:
Довести
 (використовувати нерівність Бернуллі);
(використовувати нерівність Бернуллі); (використовувати
оцінку за допомогою середнього
арифметичного).
(використовувати
оцінку за допомогою середнього
арифметичного).Знайти
 (оцінити
знизу та зверху дріб).
(оцінити
знизу та зверху дріб).Нехай
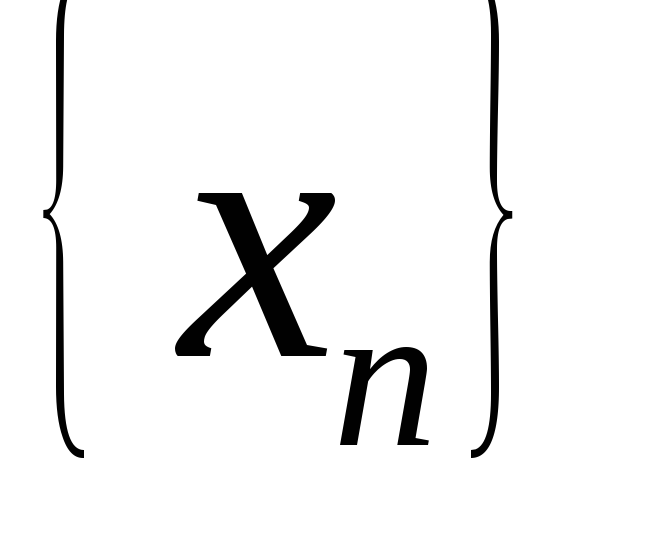 -
послідовність чисел така, що
-
послідовність чисел така, що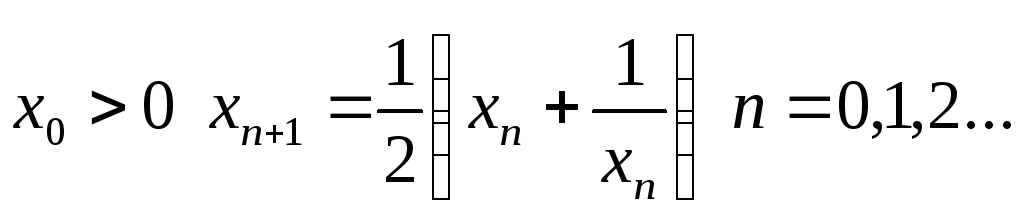 .
Довести, що
.
Довести, що
Розв’язати рівняння

Довести нерівність

Завдання для самостійної роботи.
Довести:
 2.
2.
 3.
3.
4.
![]() 5.
5.![]() 6.
6.![]()
7.
![]() 8. Знайти
8. Знайти![]()
9. Знайти
![]() ,
,![]() - будь-яке число.
- будь-яке число.
10. Нехай
![]() та
та![]() для
будь-якого
для
будь-якого![]() .
Довести, що
.
Довести, що![]()
11. Довести збіжність
послідовності![]()
12. Довести збіжність
послідовності
![]() (використовувати
(використовувати![]() ).
).
13. Довести, що
послідовність![]() розбігається.
розбігається.
Довести, що послідовності мають границю:



Знайти границю послідовності

Знайти значення виразу

Нехай
 .
Довести, що існує
.
Довести, що існує і знайти його.
і знайти його.Довести збіжність та знайти границю

Довести, що монотонна послідовність буде збіжною, якщо збігається деяка її підпослідовність.
Довести, що якщо
 , то
, то
Довести, що якщо послідовність
 не обмежена, то існує підпослідовність
не обмежена, то існує підпослідовність така,
що
така,
що .
.Якщо
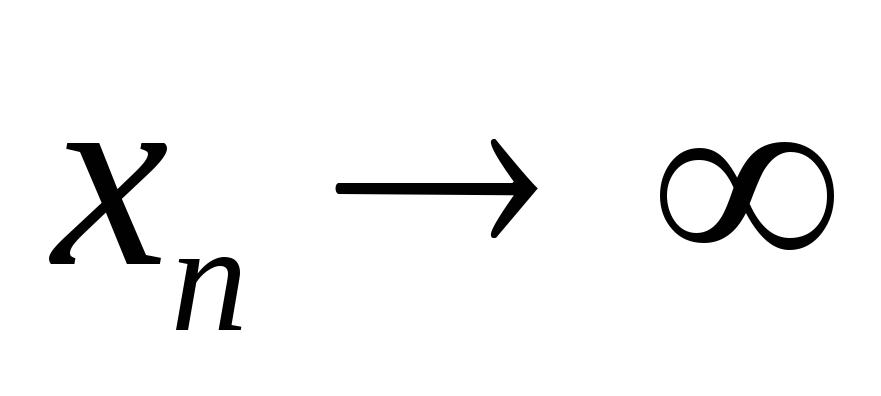 ,
то
,
то .
Довести за допомогою критерію Коші.
.
Довести за допомогою критерію Коші.Довести
 .
.
