2. Чудові границі:

1. Перша чудова границя:

Доведення. Оскільки вираз парний, то можливо припустити що>0.

S_∆AOC<S_{сектораAOC}<S_∆AOB,

S_∆AOC=

S_{сектораAOC}=, (коло R=1),

S_∆AOB=

Отримали: поділив нерівність на sinотримуємоабо

(Довести самостійно з означення).

Тоді за лемою про три границі .

2. Друга чудова границя:

Доведення. Покажемо за Гейне:

Нехай , така що. Для кожного nk_nN таке, що

(як підпослідовність ) і

Звідси, , тобто за Гейне.

Наведемо ще деякі означення границь.

Означення границь для випадку Е = F = R¹:

1.

2.

3.

Зауваження: Самостійно сформулювати означення границь для випадку Е= F= R¹ при

Лекція №12

Властивості границь. Неперервність. Розриви функцій і

1. Властивості границь функцій.

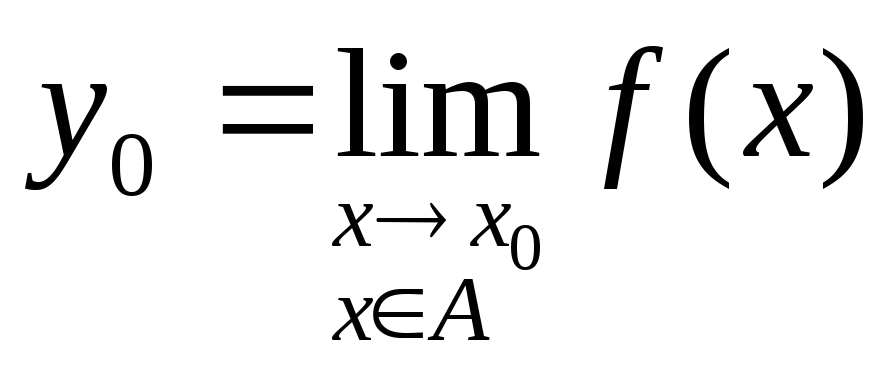Теорема 1. Нехай : X F, X, F - топологічні простори, якщо , то ₀ - єдине.

(Довести самостійно, подібно аналогічній властивості для послідовностей).

Теорема 2. Нехай : X F, X - топологічний простір, F - метризоване, і в точці_о має границю ₀ по А, тоді існує окіл U точки о такий, що множина- обмежена.

Доведення. Візьмемо в якості V (згідно означення 1 лекції №11) кулю з центром у₀ довільного радіуса R, тоді згідно з означенням границі існує окіл U точки ₀ такий, щоналежить цій кулі, тобто обмежена.

Приклад. . Якщо в х₀ має границю, то.

Теорема 3. (про границю складної функції). Нехай : X F, g : X G де X, F, G - топологічні простори. Якщо в точці x₀ має границю y₀ F, a g вточці у₀ має границю z₀ G, то складна функція в точці x₀ має границю z₀.

Доведення. Для будь-якого окола V точки z₀, , існує окіл, що. Дляокіл, щодля будь-якого околуокіл х₀ такий, що ,тобто означення границі виконується.

Розглянемо тепер більш конкретну ситуацію.

Теорема 4. Нехай : X R¹, g : X R¹ (X - метричний) і мають скінчені границі в x_о причому

мають скінчені границі при х х₀ відповідно А В,,

Доведення. Використаємо означення Гейне: для довільної послідовності , маємоза властивостями числових послідовностей, що і потрібно було довести. (Аналогічно доводяться і інші твердження).

Означення. Якщо : X R¹, де Х - метризований, то будемо говорити, що нескінченно мала величина при, якщо

Кінцева сума нескінченно малих - нескінченно мала; добуток нескінченно малої на обмежену функцію - нескінченно мала (за властивостями границь).

Означення. Дві нескінченно малі при називаються еквівалентними, якщо

Наприклад, sinх~х при .

Означення. -нескінченно мала більш високого порядку ніж () при, якщо

Наприклад. g()=, ()=, тоді g()=o( ()) при .

Теорема 5. Нехай :XR¹, g : X R¹ (X - метричний) і для кожного , тоді

Якщо : X R¹, g : X R¹, q:X R¹ і для кожного та існують

то існує границя g(x) при і

Доведення, як і властивість 4, за допомогою означення Гейне, та відповідної властивості послідовності.

Теорема 6. Нехай :ER¹, де Е, азростаюча на Е. Для того щобмала границю при (гранична для Е), необхідно і достатньо, щоб була обмежена зверху. Для того, щоб вона мала границю при(₁ гранична для Е), необхідно і достатньо, щоб вона була обмежена знизу.

Доведення провести самостійно.

2. Неперервність. Розриви.

Враховуючи означення неперервності (див. лекцію №7) і границі функції можна сформулювати висновок.

Означення. Функція ():XF неперервна в точці ₀X, якщо

З властивостей границь випливає, що всі ці властивості виконуються для неперервних функцій в точці або на всій множині X.

Зупинимось на властивості 4.

Якщо , g:XR¹, де X - метричний простір, то з неперервності в ₀ функції i g - неперервні в₀. Те ж саме можна сказати відносно складної функції.

Нехай - топологічні простори. Якщо в точці ₀ неперервна, а g неперервна в точці , то складна функціянеперервна в точці₀.

Приклад. З властивостей неперервних функцій та неперервності функцій , маємо

1. неперервна внеперервна в усіх точках, в яких знаменник не перетворюється в 0.

2. неперервна в- неперервне за виключенням точок у яких знаменник перетворюється в 0 (Q() – многочлен двох змінних).

Зупинимося на функціях :Rⁿ R¹ . Як і для границі, з неперервності розділеної по змінним, не слідує неперервність взагалі. Наприклад,

по кожній змінній неперервна в (0,0), але границі не має, тобто неперервною не є.

Означення. Якщо рівність (₀) = порушується, то говорять про розрив в точці ₀.

Нехай (): R¹→ R¹ , тоді говорять про розриви:

1. існує і скінчений, але ()не визначена в ₀ - розрив, що усувається.

2. Розриви 1-го роду зліва (зправa). Якщо = існує, але

3. Розриви 2-го роду зліва (зправa). Якщо , або не існує, або нескінченний.

Теорема. Монотонна функція має розриви тільки 1-го роду, причому не більше ніж злічене число.

Доведення спирається на теорему про границю монотонної функції. Довести самостійно.