
Пособие_ВМ_для_менеджеров
.pdf
Визначення 4.5. Головна частина приросту функції, лінійна відносно приросту незалежної змінної, називається
диференціалом функції: ¢ ∆.
¢Приріст ∆ незалежної змінної називається її диференціалом
:
∆ ¢.
Отже, остаточно маємо:
Диференціал функції дорівнює її похідної, помноженої
на диференціал незалежної змінної: |
|
¢ ¢ . |
(4.29) |
Бачимо, що якщо відома похідна, легко знайти диференціал, та навпаки, якщо відомий диференціал, відразу знаходимо похідну. Тому дії знаходження похідної та диференціала мають спільну
назву – диференціювання.
4.1.13. Властивості диференціала
Диференціали основних елементарних функцій.
За визначенням диференціала, диференціал функції дорівнює похідної, помноженої на диференціал незалежної змінної. Нам відомі похідні основних елементарних
функцій,отже, щоб знайти їх диференціали, необхідно відомі |
||
похідні помножити на диференціал незалежної змінної: |
||
¢* 9* 1¢; |
¢ 7 7 n97 ¢; |
|
¢ logm p*m1 |
¢; |
¢ "c9 de" ¢… |
|
|
161 |
Правила обчислення диференціалів
За відомими правилами обчислення похідних, знайдемо правила знаходження диференціалів:
а) диференціал алгебраїчної суми двох функцій. |
|
|
|
||||||||||||||||||||
маємо формулу для |
|
|
|
¢ |
|
|
|
|
|
|
|
|
( |
¢4 4 ¢ , ¢: : ¢ |
|
||||||||
Згадаємо похідну суми: |
|
|
|
|
|
|
4 £ (: |
. Помножимо |
|||||||||||||||
|
|
|
|
|
|
|
. |
Оскільки |
|
|
|
|
, |
||||||||||
обидві частини рівності на |
|
|
4 £ : |
|
|
|
|
|
|||||||||||||||
|
|
|
|
обчислення |
диференціалу |
алгебраїчної |
|||||||||||||||||
суми: |
|
|
¢ 4 £ : ¢4 £ ¢:. |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
б) диференціал добутку двох функцій. |
( |
( |
|
|
|
|
|||||||||||||||||
Згадаємо |
похідну |
добутку: |
|
|
|
|
|
|
|
|
. |
||||||||||||
¢: : ¢: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оскільки |
|
|
|
|
||
Помножимо обидві частини рівності на |
|
|
4. · : 4 · : 4 (· : |
||||||||||||||||||||
|
, маємо |
|
|
|
|
|
|
|
|
|
обчислення |
диференціалу |
|||||||||||
добутку |
формулу |
|
для |
|
|
|
¢ |
|
|
|
¢4 4 ¢ , |
||||||||||||
|
¢ 4 · : : · ¢4 4 · ¢:. |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
в) диференціал частки двох функцій. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
5 |
|
( |
|
5 ; 5;( |
|
|
|
|
|
|
|
||||||
формулу для |
¢ |
|
|
|
|
|
|
|
|
S |
|
|
|
|
:¢: : ¢ |
|
|
|
|||||
|
|
|
|
|
¢4 4 ¢ , |
|
обидві |
||||||||||||||||
Згадаємо похідну |
частки: |
|
|
|
|
V |
; |
|
|
|
. |
Домножимо |
|
||||||||||
частини рівності на . |
Оскільки |
|
|
|
|
|
( |
|
|
|
|
, |
маємо |
||||||||||
|
,;- |
|
|
|
|
|
|
|
|
|
|
||||||||||||
обчислення диференціалу частки
¢,5- ;œ5 5œ;
;;S .
Диференціал складної функції. Інваріантність диференціала.
Нехай дано функції |
|
і |
|
- |
неперервні і |
|||
|
|
|
своїх аргументів Похідна функції за |
|||||
диференційовані функції |
|
4 |
|
4 . X |
|
обчислення |
||
змінною |
|
знаходиться |
за |
формулою |
(4.11) для |
|
||
|
складної функції |
|
|
|
|
|
||
похідної |
|
|
: |
|
|
|
|
|
|
|
|
|
162 |
|
|
|
|
|
|
( 5( · 4( . |
|
|
|
|
Помножимо обидві частини рівності на ¢ ,отримаємо |
|
|
||||
Згадаємо, що |
¢4 4 ¢ |
¢ 5( · 4( ¢ . |
|
|
|
|
¢ 5( · ¢4. |
|
|
|
(4.30) |
||
( |
,звідси маємо |
|
|
|
|
|
Тобто бачимо, що диференціал функції |
|
має такий же |
||||
|
|
|
змінною функції |
. |
||
самий вигляд, якщо б 4 була незалежною 4 |
|
|
||||
Ця властивість |
має назву інваріантності |
форми |
||||
диференціала від аргументу функції.
Диференціал функції 4 має4 незмінний вигляд в незалежності від того, чи є її аргумент незалежною змінною або функцією незалежної змінної.
Приклад 4.21. Знайти диференціал функції
7 < 2n9 j 2klf · 7td"c95 .
Розв’язання:
¢ 7¢ < 2¢Dn9 j H 7td"c95 · ¢ 2klf2klf · ¢ 7td"c95 35 A¢ 2 · vw1 · klf1S ¢
7td"c95 · 2klf · n92 · "c9 ¢ 2klf · < ¢
√1 B< S
,35 A A 7td"c95 · 2klf · n92 · "c9 <·B{|}2 - ¢
fg*B √1 B< S .
163

4.1.14. Застосування диференціалу у наближених обчисленнях
Згадаємо, що приріст функції визначається за формулою
∆ l ∆ l .
Явний вираз приросту функції може бути виражений через приріст аргументу досить складною формулою. Спробуємо
замінити приріст функції його диференціалом:
∆ l ∆ l ¤ ( l¢ ¢
похибка цієї заміни мала (див. п. 4.1.12). |
|
|
|
¢ |
|
||||||
наближене значення |
l ¢ |
знайдемо l, l,: |
|
||||||||
Отже, |
якщо |
|
|
( |
|
, то |
|||||
відомі |
значення |
|
|||||||||
|
|
|
|
|
|
за формулою |
|
|
|||
|
|
l ¢ ¤ l |
( l¢ |
|
|
(4.31) |
|||||
|
|
|
|||||||||
Приклад 4.22. Знайти наближене значення функції |
|
||||||||||
< 2A |
7B 15, коли 1,003. |
1, ¢ 0,003. |
|||||||||
Розв’язання: |
Приймаємо |
||||||||||
Обчислимо значення функції у точці |
1: |
||||||||||
|
1 1 2 7 15 21. |
|
|
||||||||
Знайдемо похідну функції |
|
|
|
|
|
|
|||||
|
|
( 5A |
8= 14. |
|
|
|
|
||||
Обчислимо її значення у точці 1: |
|
|
|
|
|
||||||
|
( 1 |
5 8 14 11. |
|
|
|||||||
Скористаємося формулою (4.31), остаточно маємо:
1,003 ¤ 1 0,003 21 11 · 0,003 21,033.
164
7tdde"0,4991. |
|
|
|
|
Приклад 4.23. |
Знайти пнаближене значення функції |
|||
. |
|
|
7tdde" 0,5: |
¢ |
0,0009 |
|
|
0,5 |
|
Розв’язання: |
Приймаємо |
, |
|
|
Обчислимо значення функції у точці
0,5 7tdde"0,5 u ¤ 1,0472
= .
Знайдемо похідну функції
( √11 S.
та обчислимо її значення у точці |
|
|
||||||
( |
|
|
( |
0,5 |
|
1 |
B |
. |
|
|
|
|
√1 ,B< |
√= ¤ 1,1547 |
|||
Скористаємося формулою (4.31), остаточно маємо:
7tdde"0,4991 ¤ 0,5 0,0009 1,0472 1,1547 ·0,0009 1,0482.
|
|
|
4.1.15. Геометричний сенс похідної і диференціалу |
|
|
|
||||||||
|
|
|
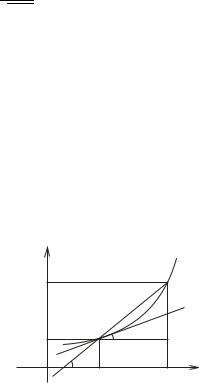
Нехай функція |
|
|
|
|
|
|
|
|
|||
визначена |
на інтервалі і |
y |
|
|
M |
L |
|
|||||||
неперервна в точці |
|
|
Нехай |
f(x0+ x) |
|
|
|
|
||||||
|
. 7, Ž |
|
|
|
|
|
||||||||
відомі |
точки |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
та відомо |
|
|
|
|
|
|
||
що |
|
|
|
|
, ¥ , ,, |
|
M0 |
α0 |
|
|
|
|||
¥ ∆ , ∆ . |
|
|
|
f(x0) |
|
|
|
|
||||||
|
|
∆ • 7, Ž |
|
|
|
α |
|
|
|
|
||||
|
|
|
Проведемо |
січну |
|
|
|
|
|
x |
||||
( |
рис |
. 4.1). |
Вона |
визначається |
O |
x0 |
|
x0+ |
x |
|||||
|
|
|||||||||||||
|
|
|
|
|
¥ ¥ |
|
|
|
|
|
|
|||
рівнянням |
|
|
¦ , |
Рис. 4.1. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
165 |
|
|
|
|
|
|

кутовий коефіцієнт якої дорівнює |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
¦ j§ ∆∆. |
|¥ ¥| |
|
|
|
|
|
|
|
|||||||||
і |
|
¥ |
прямує до нуля. |
|
∆ 0, |
|
|
|
|
|
|
|
|
|
|||||||||||||
¥ |
|
|
|
|
|
|
|
|
|
|
відстань |
|
|
|
|
|
|
|
|||||||||
|
|
Покажемо, що при |
|
|
|
|
|
між точками |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Дійсно |
з неперервності функції |
|
|
|
||||||||||||
|
при |
|
|
|
маємо |
lim∆ ∆ 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Тобто, при ∆ 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
∆ B 0. |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|¥ ¥| [ ∆ B |
|
|
|
∆ |
¦ |
|
||||||||||||||
то пряма лінія, рівняння якої ми |
|
|
lim |
∆ |
¦ lim |
|
|
д, |
|||||||||||||||||||
Отже, якщо існує кінцева границя |
|
. |
|
|
|
|
∆ ∆ |
|
|
|
|||||||||||||||||
¦ |
|
|
∆ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
отримуємо з рівняння |
|||||||||||||||||
|
|
|
|
|
при |
|
|
|
|
називається |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
(рис. 4.1) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дотичною до |
|||||||
графіку функції |
¥ . |
|
|
|
в точці |
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Бачимо, |
що дотичною до графіку функції |
|
|
|
|
|
в |
||||||||||||||||||
|
|
|
|
називається граничне положення січної, |
якщо точка |
|
|
||||||||||||||||||||
точці |
|
|
|
|
|
|
|
||||||||||||||||||||
прямує до точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
З розв’язання цієї задачі прямує геометричний сенс |
|||||||||||||||||||||||||
похідної, а саме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Визначення 4.6. Значення похідної функції |
|
у |
|||||||||||||||||||||||
точці дотику |
дорівнює кутовому коефіцієнту |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
точці |
|
|
|
|
|
|
|
|
|
|
|
дотичної до |
|||||||||
кривої в цієї |
|
: |
|
|
|
|
¦д , |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.32) |
|||||||||
а рівняння дотичної має вигляд: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.33) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
166

lim |
( ¦ . lim |
∆ |
∞ |
|
то |
|
|
Зауваження. |
∆ |
, |
|||
|
|
|
Якщо |
|||
пряма∆рис 4.2),∆рівняння якої |
|
|||||
|
, |
|
|
|
|
|
січної, |
|
∆ 0 |
|
|
- |
|
отримуємо при |
|
|
з рівняння |
|||
|
називається |
вертикаль |
||||
функції в точці . |
|
|
||||
ною |
дотичною |
до |
графіку |
|||
y
M L
f(x0+ x)
f(x0) M0
|
α |
x |
|
O |
x0 x0+ x |
||
|
Рис. 4.2.
Близько пов’язане з поняттям дотичної, поняття нормалі до кривої
Визначення 4.7. Нормаллю до кривої в точці
називається пряма лінія, перпендикулярна до дотичної у точці дотику..
З умови перпендикулярності прямих (2.22) знаходимо
кутовий коефіцієнт нормалі 1 |
1 |
, |
|
|
(4.34) |
|
|
¦н ¬д ( a |
|
||||
отже шукане рівняння нормалі має вигляд |
|
|||||
|
( 1a |
|
. |
(4.35) |
||
|
|
|||||
Приклад 4.24. Записати рівняння дотичної до кривої
2= 3B 8 13
в точці з абсцисою 3.
Розв’язання: Знайдемо похідну функції
( 6B 6 8.
і обчислимо значення функції та її похідної в точці :
167
3 2 · 3= 3 · 3B 8 · 3 1354 27 24 13 38;
( (3 6 · 3B 6 · 3 8 44.
Скористаємося формулою (4.33) і отримаємо шукане рівняння
дотичної
38 44 3;44 94.
Приклад 4.25. З’ясувати, в яких точках кривої
= 12
A 2
її нормаль паралельна прямій = .
Розв’язання: За умовою паралельності (2.21) кутові коефіцієнти нормалі та заданої прямої повинні дорівнювати
одне одному: |
|
|
¦н ¦. |
|
|
|
|||
|
|
|
|
|
|
||||
Знайдемо похідну функції ( =S, |
|
|
|||||||
|
|
|
|
|
|
¦н |
( a = |
||
Отже кутовий коефіцієнт нормалі |
|
|
1 |
S |
|||||
і скористаємося умовою паралельності |
1 |
2 |
|||||||
|
|
A |
|
B |
4; |
|
|||
= |
= ; |
|
|
‹ B |
2 Π|
||||
|
S |
|
|
|
|
|
|
|
. |
Виявилося, що точок, які задовольняють умові, дві. Їх ординати знайдемо, підставивши знайдені абсциси до рівняння кривої:
168
|
|
|
|
|
|
|
3 |
|
|
|
27 |
, |
|
|
|
|
|
|
|
|
|
|
|
- |
1 2 |
12 2 |
Π|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
3 |
|
|
|
21 |
|
|
|
|
|
|
|
||
|
|
|
|
|
B 2 12 2 . |
|
|
|
|
|
|
|
|
||||||
Отже, |
|
в |
точках |
¥1 , 2, BYB -, |
¥B ,2, B1B - |
нормаль до |
|
кривої |
|||||||||||
= |
12 паралельна прямій |
|
=A 2. |
|
|
|
|
¢ |
|||||||||||
дорівнює довжині |
|
j§. |
|
|
|
|
|
|
|||||||||||
|
|
З’ |
ясуємо |
геометричний |
|
сенс диференціала функції |
|||||||||||||
¢ |
(рис. 4.3). Так як |
( |
|
|
®¯ |
, то диференціал |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
, |
|
|
|
відрізку |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Визначення 4.8. Диференціал |
|
функції |
|
|
|
|
в |
||||||||||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
точки |
||||
|
|
|
|
|
|
|
|
|
|
приростом ординати |
|
|
|||||||
точці |
|
|
може бути |
зображений |
|
|
°‘ |
|
|
|
|
|
|
||||||
D, H |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дотичної |
яка проведена до лінії |
|
|
|
|
у відповідній точці |
|||||||||||||
|
|
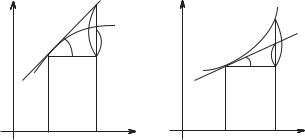
Зауваження. |
Диференціал |
функції |
функції |
|
|
у |
|||||||||||
відповідній точці може бути як більше приросту |
|
|
|||||||||||||||||
(рис. 4.3,а), так і менше його (рис. 4.3,б). |
|
|
|
|
|
|
∆ |
||||||||||||
y |
|
|
M |
T |
|
y |
|
|
M |
|
|
|
|
|
|
|
|
|
|
||
1.3.13. |
|
α |
dy |
y |
|
|
|
|
T |
y |
1.3.14. M |
|
R |
|
|
M |
α |
dy |
|
||
1.3.15. |
|
|
|
|
|
|
|
|
R |
|
1.3.16. |
|
|
|
|
|
|
|
|
|
|
|
x |
x=dx |
|
|
|
x |
x=dx |
x |
||
O |
(а) |
x+dx |
x |
O |
(б) |
x+dx |
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 4.3. |
|
|
|
|
|
169
4.1.16. Фізичний сенс похідної та диференціалу
|
|
|
Згадаємо, що поняття похідної |
|
ми |
|
вводили, |
коли |
||||||||||||||||||||||
розв’язували задачу про швидкість зміни функції: |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
lim∆ |
∆ . |
|
|
|
|||||||||
|
|
lim∆ сер. lim∆ ∆ |
|
|
∆ |
|
|
|
||||||||||||||||||||||
|
|
|
Нехай |
|
|
|
|
час |
|
- закон руху матеріальної точки, |
|
- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Нехай |
|
- |
координата точки в момент |
|||||||||||||
довжина шляху", -" |
|
¥1 |
|
|
|
|
|
|
|
|
|
|
|
" |
|
|||||||||||||||
часу |
|
, а |
|
|
і |
- в |
момент часу |
|
; |
|
|
- |
довжина шляху між |
|||||||||||||||||
точками |
|
|
|
|
|
|
, |
тобто |
|
|
∆ |
∆" |
|
|
. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
¥B |
¥B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
¥1 |
|
|
|
|
∆" " ∆ " |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Відношення ∆f∆v є середня швидкість руху на відрізку від |
|||||||||||||||||||||||||||
|
до |
|
B |
, |
|
|
|
∆v |
∆f - |
миттєвою швидкістю в момент часу , |
||||||||||||||||||||
тобто1 |
|
|
lim |
∆v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
¥ |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
: lim∆v ∆f∆v ". |
|
|
|
|
|
|
(4.36) |
||||||||||
|
|
|
За визначенням диференціала, |
|
|
|
|
|
|
|
|
, з цього прямує, |
||||||||||||||||||
що диференціал шляху дорівнює |
відстані |
|
|
|
яку б пройшла |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢" :¢, |
|
|
|
|
|||||||
матеріальна точка за проміжок часу |
|
|
|
від моменту |
|
до |
||||||||||||||||||||||||
моменту |
|
|
|
|
|
|
, |
|
якщо б рухалася рівномірно з швидкістю |
яка |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
. |
|
|
, |
|
|
|||
|
|
|
|
|
миттєвої швидкості точки в момент |
|
|
|
|
|
||||||||||||||||||||
дорівнює ∆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Аналогічно, прискорення руху – |
|
це |
|
швидкість |
зміни |
||||||||||||||||||||||
швидкості |
|
|
|
|
|
|
7 lim∆v ∆;∆v :( ", |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(4.37) |
||||||||||||||||||
тобто обчислюється за другою похідною від закону руху матеріальної точки
Приклад 4.26. Відомий закон руху матеріальної точки
" = A 1 = 7B 18 5
A = .
170
