Пособие_ВМ_для_менеджеров

lim-Dm

j

y

j

-S) V( -() V

V

j

y

Vj

M

L € -S)

S € -S)

€ -()

S € -S)

lim-Dm

j

y

-VS8-S)(-VS8-()

j

y

j

Vj

V

M

L € -S)

S € -S)

€ -()

S € -S)

lim-Dm

j

y

j

-

V

j

y

.

Vj

M

L € -S)

S € -S)

€ -()

S € -S)

limgD' ƒ„Agg 1.

(3.10)

Доведення: Будемо виходити з

A B

геометричного

визначення

синуса

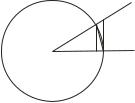
(рис. 3.9). Беремо коло з одиничним

радіусом і кут [

в радіанах

0 [

…8.

O

α

D C

Функція

ƒ„Ag

- парна, а тому достатньо

розглянутиg

випадок

,

коли

[ 0.

З

Рис. 3.9.

рис. 3.9 бачимо, що

†∆ˆo‰ †сектораˆo‰ †∆ˆp‰.

Площі обраних фігур наступні:

†∆ˆo‰

8) ‘ · * 8) ’ · ’ · ./0[;

†

8

*‘ · ’ 8 [ · ’ · ’

сектораˆo‰

)

“

)

;

†∆ˆp‰ 8) ‘ · +‘ 8) ’ · ’ · 6 [.

Тобто можна записати

1

1

1

’ · ’ · ./0[

’ · ’ · 6 [

2

2 [ · ’ · ’ 2

з цього прямує, що ./0[ [ 6 [.

Скоротимо всі члени нерівності на ./0[ 0, отримаємо

1 ƒ„Agg ”•)ƒg

або 5 .[ ƒ„Agg 1.

limgD' 5 .[ 1,

що

З геометричного визначення косинуса зрозуміло,

звідси з теореми про стиснуту змінну остаточно маємо

112

lim-D'

-

Приклад

3.12. Обчислити границю функції

ƒ„Af-

.

Розв’язання:

'

f·ƒ„Af-

ƒ„Af-

lim-D'

ƒ„Af-

· lim-D'

-

K'K lim-D'

f·-

f-

— · 1

.

– D 0

lim-D'

ƒ„Ah-

Приклад

3.13. Обчислити границю функції

ƒ„Af-.

Розв’язання:

ƒ„Af-

'

-·ƒ„Af-

lim-D' ƒ„Ah-

K'K lim-D' -·ƒ„Ah-

lim-D'

ƒ„Af-

· lim-D'

-

hf.

-

ƒ„Ah-

lim-D'

-

Приклад

3.14. Обчислити границю функції

>˜f-

.

Розв’язання:

lim-D'

>˜f-

K''K lim-D'

ƒ„Af-

·

)

lim-D'

ƒ„Af-

·

-

-

”•ƒf-

-

· lim-D' ”•ƒ)f- · 1 .

lim-D'

-

Приклад 3.15. Обчислити границю функції

f™”ƒ„A-.

lim-D'

ƒ„AVU-(ƒ„AV-.

k-V

Розв’язання:

ƒ„AU-(ƒ„A- ƒ„AU-Sƒ„A-

lim-D'

ƒ„AVU-(ƒ„AV-

lim

k-V

k-V

-D'

lim-D'

8ƒ„A8-”•ƒ -·8ƒ„A -”•ƒ8-

k-V

lim

-D•

…

|

|

…8

Ÿ

V

L8

M · 6 0 · ∞ ž

D 0

limœD' · 6 L…8 M limœD' · 56

limœD'

œ·”•ƒœ

œ

.

ƒ„Aœ limœD'

ƒ„Aœ · limœD' 5 . 1 · 1 1

1)

lim-D'

>˜-- 1;

2)

lim-D'

f™”ƒ„A-

1

;

-

3)

lim-D'

f™”>˜-

1

;

-

4)

lim-D'

ƒ„Af- -

;

5)

lim-D'

ƒ„Af-

f.

ƒ„Ah-

h

Друга важлива границя

Теорема. Функція

A

L1 " AM

A має границю при

)

0 D ∞.

) A

A )

A A()

)

A A() A(8

)

) .

L1 " AM 1 " )! · A "

8!

· AV "

!

· Aj " \ " AJ

Перетворимо праву частину

)

)

8

) A

)

)

L1 " AM

1 " 1 " )·8 L1 AM " )·8· L1 AM L1 AM " \

)

)

8

A() .

" )·8· ·…·A L1 AM L1 AM … L1

A M

0

Бачимо,

що функція

L1

" AM

зростаюча при зростаючому

.

) A

)!

8·)

на

8·8)

8)V,

)! 8·)· на 8·8·8) 8)j,

…

)

)

на

)

) ,

A!

8· ·…·A

8·8·…·8

8JqW

звідси

) A

)

)

)

) .

8)J , 8J¡W)

L1 " AM

1 " 1 " 8 "

8V "

8j " \ " 8JqW

, … ,

дописавши в праву частину члени прогресії

Тим

більше,

отримаємо

) A

)

)

)

)

.

L1 " AM 1 " L1 " 8

" 8V " 8j " \ " 8J

" \ M

)

A

.

0 1

L1 " AM

3

Якщо

ліва частина нашої формули дорівнює 2. Отже

,

остаточно маємо

) A

3

.

2 L1 " AM

Визначення 3.23. Числом

= називається

границя

limADm L1 " AM

= ¢ 2,718 …

.

)

A. Воно приблизно дорівнює

Теорема.

Функція

lim-Dm L1 " -M

-

при

D ∞

має

)

границю, яка дорівнює =:

-

=

lim-Dm L1 " -M

.

(3.11)

)

Доведення цієї теореми виходить за межи вивчаємого

курсу.

Зауваження. За допомогою другої важливої границі

розкриваються невизначеності типу 1m.

Приклад 3.18. Обчислити границю функції

-.

lim-Dm L1 " -M

Розв’язання. Скористаємося другою важливою

границею:

-Dm

-

| m|

-Dm

c

.

lim

£lim

L1 "

y

¤

=

L1 " -M

1

-M

Приклад 3.19. Обчислити границю функції

lim-Dm L1 " -(8k MU-.

Розв’язання.

-Dm

k

U-

|

m|

-Dm

k

cqV

x

·U-

lim

L1 "

x

¤

cqV

L1 " -(8M

1

£lim

-(8M

lim-Dm L1 "

-( ( -(U

l-()

-SU

M

£lim-Dm L1 "

yc¡!

yc¡!q}

· l-()

-(HSUM q}

¤

q} zcqW

=()8.

=`abcD¥ yc¡!

!cqy

¤

!cqyz · 8-S

0 £lim-Dm L1 " U-l( M

z

0=`abcD¥

z Vc¡j

0=

WV

)8U 0= )8U .

!cqy

!

118

U-(8

))-(

U

m

0

.

lim-Dm Lk-SlM

LkM

Три важливі границі

Теорема 1. Справедлива формула

lim-D'

¦A )S-

1

.

(3.12)

-

маємо, що

WДоведення: З другої

важливої границі

1 " § при D 0 прямує до =, отже маємо

.

¦A )S-

c

ªªªªªªªªªªªªªªªªªªªªª«

-

W

при D 0

0= 1

0 – 1 " —

Що і треба було довести.

Теорема 2. Справедлива формула

lim^D' f¬^() 0 .

(3.13)

Доведення: Якщо

, то величина

^ 1

^

, тобто

в чисельнику величина

нескінченно мала Нехай

$ D 0

.

1 D 0

119

З теореми 1 прямує, що ~ 0 1 " тобто

^ 1 ~ 0 1 " ^ 1 0 ^ $ · 0 ,

з цього прямує, що

lim^D' f¬^() lim^D' ^·¦Af^ 0 .

Що і треба було довести.

Теорема 3. Справедлива формула

lim^D'

)S^ ®()

.

(3.14)

^

Доведення: Величина

f

при

прямує до

нуля, тобто є величиною

нескінченно малою

Як і при доведенні

1 " $

1 .

$ D 0

теореми 2 положимо 1 " $ f

1 .

З цього прямує ~ 0 1 "

, тобто

1 " $ f 1

~

~

0¯1 " 1 " $ f 1 ° 0 1 " $ f · 0 1 " $ .

lim^D'

)S^ ®()

lim^D'

f·¦A )S^

.

^

^

lim-D'

¦A )Sk-

)

· lim

k¦A )Sk-

k.

-

k-

-D'