Пособие_ВМ_для_менеджеров

Аналогічно можна переконатися, що при зміні знакапохідної з на і при переході через зліва направо точкає точкою мінімуму функції.

4.4.3. Схема дослідження функції на монотонність та екстремум

Вкажемо послідовність дій для з’ясування інтервалів монотонності та екстремумів функції як в кінцевому, так і в нескінченному інтервалі.

1.З’ясуємо область визначення функції (ОВФ).

2.Знайдемо( критичні0 точки, похідна в яких дорівнює нулю або не існує.

3.Нанесемо на числову вісь (або в таблицю) точки, похідна в яких дорівнює нулю або не існує, та точки, в яких функція не існує. Таким чином ми розіб’ємо числову вісь на часткові інтервали, в кожному з яких похідна не змінює знак. Ці інтервали є інтервалами монотонності функції.

4.З’ясуємо знак похідної в кожному з часткових інтервалів, для цього достатньо встановити знак у

будь-якій точці обраного інтервалу. За знаком похідної визначаємо характер поведінки функції( · 0в кожному з інтервалів монотонності( ¸ 0: якщо , то функція зростає, якщо - спадає.

193

5.Прослідкуємо за зміною знака похідної при переході зліва направо через границі інтервалів монотонності функції і з’ясуємо, які з критичних точок є мінімумами, а які – максимумами. Може так статися, що деяка точка не є точкою екстремуму функції. Це може статися, якщо в двох суміжних інтервалах, які

поділяються вказаною критичною точкою, похідна має однаковий знак.

6.Підставимо у функцію значення незалежної

1 0, B =B.

З’ясуємо знак першої похідної в отриманих часткових інтервалах, встановимо характер поведінки функції. Результати досліджень зведемо у таблицю:

194

або на числову пряму (рис. 4.8):

рис. 4.9. Отже, для знаходження найбільшого і найменшого значення функції необхідно:

195

1.Розв’язати задачу на екстремум функції.

2.Обчислити значення функції в точках екстремуму (лише тих, що належать обраному інтервалу) і на кінцях інтервалу.

3.Порівняти отримані значення і обрати з них найбільше та найменше.

Окремо розглянемо задачки, в яких дві величини пов’язані функціональною залежністю, і потрібно знайти значення однієї з них (це значення може бути або обмеженим певним інтервалом, або необмеженим), при якому інша приймає найбільше або найменше значення. Для розв’язання таких задач необхідно скласти рівняння, яке описує функціональну залежність цих величин, а потім знайти найбільше або найменше значення функції за описаною схемою.

Прикладln 4.41. ЗнайтиÀoнайбільше=; 1Á і найменше значення функції в інтервалі .

Розв’язання:

Проведемо дослідження функції на екстремум:

ОВФ: · 0 або • 0, ∞ .( 1 · ln · 1 ln 1

;

( 0; ln 1 0; ln 1; o 1 1z.

Критична точка належить досліджуваному інтервалу. Обчислимо значення функції в критичній точці і на кінцях

інтервалу:

o = o = ln o = z1M ln o = z=M ln o,1z- 1z ln o 1 1z ln o 1z;

196

Приклад 4.42. Визначити, при яких розмірах відкритого басейну з квадратним дном, на облицювання стін і дна буде затрачено найменшу кількість матеріалу. Об’єм басейну фіксований.

197

4.4.5. Опуклість та угнутість функцій. Точки перегину

Визначення 4.14. Дуга називається опуклою, якщо вона перетинається з будь-якою своєю січною не більш, ніж в двох точках.

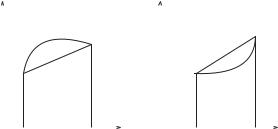
Якщо дуга опукла, вона цілком розташована по одну сторону від дотичної, проведеної в будь-якій точці. Опукла дуга може обертатися як опуклістю вгору (рис. 4.10, а), або донизу

(рис. 4.10, б).

Лінії, обернені опуклістю вгору, називаються опуклими (опукла дуга розташована під дотичною); лінії, обернені опуклістю донизу, називаються угнутими (опукла дуга розташована над дотичною).

Особливу роль грають точки, які відділяють інтервали опуклості і угнутості функції.

Визначення 4.15. Точкою перегину функції називається точка лінії, яка відділяє опуклу дугу від угнутої.

В точці перегину функції дотична перетинає лінію; в околі цієї точки лінія розташована по обидві сторони від дотичної.

198

З’ясуємо ознаки опуклості та угнутості функції та умови існування точок перегину.

рівнянням є

де 1 ¸ Ù ¸ ¸ Ú ¸ B.

Знов скористаємося теоремою Лагранжа:

199