Пособие_ВМ_для_менеджеров

lim-D'

)Uc(Uc

lim-D' L

)Uc()

Uc()

M 015 05

-

-

-

0 )UU

03.

x

)

W

()

) )

)

√)S-()

)S-

lim-D'

lim-D'

-

x

· k

8)

-

.

3.2.7. Порівняння нескінченно малих

Нехай декілька нескінченно малих величин

є

функціями одного ж того ж самого аргументу

и прямують до

нуля при

D

(або

).

[, e, ± …

D ∞

[ i

e

Визначення 3.23

Якщо відношення

має кінцеву і

відмінну від нуля границю. при

D

, тобто

lim-Df ig * d 0,

а

lim-Df ig o) d 0,

То [ і e нескінченно малі одного порядку малості.

Приклад

3.26.

Нехай

малі

,

їх

,

де

-

нескінченно

[ . 1 5 .

e ·

відношення

./05

: D 0

)(”•ƒ- )S”•ƒ-S”•ƒV-

lim-D'

)(”•ƒj-

'

lim-D'

-·ƒ„AU-

K'K

-·ƒ„AU-

lim-D' )(”•ƒ-

· lim-D' 1 " 5 . " 5 .8

-·ƒ„AU-

121

8ƒ„AVc

ƒ„Ac

ƒ„Ac .

3 · lim-D' -·ƒ„AUV- 6 · lim-D'

- V · lim-D' ƒ„AUV-

6 · 8) · )U²8 )'.

3.23

[ і e

порядку.

нескінченно малі

одного

Згідно з визначенням

Визначення 3.24. Якщо lim-Df ig 0, а lim-Df ig ∞, то

нескінченно мала

[

вищого порядку, ніж нескінченно мала

; а

нескінченно мала

нижчого порядку малості, ніж

нескінченно

e

мала [

при D .

e

[

-j

, e

-y

Приклад

3.27. Нехай

де

D ∞

-V()

-VS),

- нескінченно малі. Обчислимо границю їх відношення:

g -

cVqW

'

-y -V()

cj

.

lim-Dm i -

lim-Dm cV¡W

K'K

lim-Dm -j -VS) ∞

e

cy

[ -

3.24

нескінченно мала

нижчого

Згідно з визначенням

порядку, ніж

.

якщо e

Визначення 3.25. Нескінченно мала

називається

[´

-го порядку відносно

D

,

нескінченно малою

нескінченно малої

e

якщо

і

-

нескінченно малі одного порядку при

,

тобто

³

[

lim-Df giµ * d 0.

e

Приклад 3.28. З’ясувати порядок відносно

функції

!

-j-S), нескінченно малої при D 0.

,

³ 2.

Розв’язання: Порівнюючи степені

положимо

Обчислимо границю:

122

Зауваження 2. Нескінченно великі величини

порівнюють між собою так само, як і нескінченно малі.

5

" 12

- нескінченно великі

[ 7 .

" 4 e

:

3.31. Нехай

D ∞

і

Приклад

при

Знайдемо границю їх

відношення

7 " 4

∞

7

-limDm 5 " 12

K∞K

обчислення границь:

6 ~ ;

./0 ~ ;

45./0 ~ ;

456 ~ ;

0 1 " ~ ;

=- 1~ .

lim-D' ¶jc()

Приклад 3.32. Знайти границю функції

f™”>˜k-.

Розв’язання:

Скористаємося

еквівалентними

нескінченно малими

124

lim-D'

f™”>˜k-

'

456 7 ~7

k-

k.

¶jc()

K'K · = - 1~3

¸ lim-D' -

y+

y

Визначення 3.27.

Приростом

y

функції

в

даній

точці

'

y

M

∆ " ∆ ( . 3.10).

∆

називається різниця

приріст аргументу'

рис' ,

де

-

0

y M0

N

,

3.28.

Функція

x

Визначення

0

називається неперервною у

точці

якщо ця функція визначена

деякому'

lim∆-D'

∆ 0

околі

Рис. 3.10.

x

у

'

,

O

0

x+ x

виконується умова:

.

0

2

-

Приклад

3.33.

Перевірити

чи

є

функція

неперервною у будь якій точці

'.

Розв’язання: Знайдемо приріст функції ∆:

∆ 2-NS∆- 2-N 2-N · 2∆- 2-N 2-N2∆- 1.

Отже при ∆ D 0,

2∆- D 1, ∆ D 0 , тобто функція неперервна.

Скористаємося визначеннями 3.27, 3.28 і дамо ще одне

визначення неперервності функції в точці. Для цього приріст

функції ∆ перепишемо як

lim∆-D' ' " ∆ ' 0

або

lim∆-D'

' " ∆ lim∆-D' ' .

∆ D 0)

остаточно маємо

' " ∆ ,

то

D '

(

при

і

Якщо ввести позначення

125

lim-D-N ' .

(3.15)

Визначення 3.29. Функція

неперервна в точці

, якщо вона визначена в будь-

якому околі цієї точки і якщо

,

границя'

функції існує і дорівнює значенню функції при

'

(за умовою, що незалежна змінна

прямує до ').

Визначення

,

якщо вона

-

3.30.

Функція

називається

неперервною в інтервалі

неперервна у будь якій

точці інтервалу.

точці ºn

;

Однобічна неперервність

,

визначена на

Визначення 3.31

Нехай функція

інтервалі

.

Кажуть.

, що функція

неперервна в

ліворуч'

якщо

lim-D-N(' ' .

(3.16)

. Кажуть, що функція

º

;

,

Визначення 3.32.

Нехай

визначена на інтервалі

праворуч'

неперервна в точці

n

якщо

lim-D-NS' ' .

(3.17)

126

точка

належить

,

;

і

Якщо функція

визначена на інтервалі

функції в'

цьому інтервалу то для

неперервності

точці

необхідно і достатньо, щоб функція

була неперервна ліворуч'

і праворуч від точки ':

lim-D-N(' lim-D-NS' .

(3.18)

Класифікація розривів

Визначення 3.33. Якщо функція

не визначена в

величини то кажуть

,

що в

точці

або має стрибок кінцевої

,

,

така точка , в якій

Тобто,

точці

'

функція

має

розрив першого роду.

точкою'

функції

першого

роду називається

розриву

між собою (рис'

функція має ліву та праву границю не рівні

. 3.11):

lim-D-N(' d lim-D-NS' .

(3.19)

Визначення 3.34. Якщо функція

'

в точці

'

не

роду (рис. 3.12).

має хоча в однієї з однобічніх границь,

або вона дорівнює

,

то кажуть, в функція

має в точці

розрив

v∞

другого

y

y

O

x

O

x

Рис. 3.11.

Рис. 3.12.

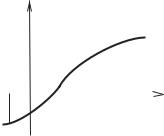
Приклад 3.34. Перевірити на неперервність функцію

" 5,

0

» 8,

0 2

y

5 6,

2

9

Розв’язання:

y=5x-6

Побудуємо

графік

5

функції (рис. 3.13):

y=x+5

Функція

задана

трьома

y=x 2

елементарними

функціями,

неперервними

у

своїх

-

5

O

2 3

x

областях визначення, тому,

Рис. 3.13.

якщо вона і має розриви, то

лише у

точках

0

і

2.

Дослідимо на

неперервність

функції у точках:

lim-D'('

lim-D'(' " 5 5;

lim-D'S'

lim-D'S'

8 0;

lim-D'('

d lim-D'S'

;

lim-D8('

lim-D8('

8 4;

lim-D8S'

lim-D8S'5 6 4;

lim-D8('

lim-D8S'

.

0

Отже, у точці

роду

функція неперервна,

а у точці

має

розрив першого 2.

Приклад

3.35. Перевірити

на

неперервність функцію

5

x

у 4

cqy в точці

.

Розв’язання: Обчислимо ліву та праву границю функції

у точці 4:

x

5x

x

5

0

lim-D (' lim-D (' 5 x

(m

cqy

(N

;

lim-D S' lim-D S' 5cqy 5N 5m ∞.

Отже, права

границя

функція

у

точці

дорівнює

нескінченності, а тому вона має в ній розрив

другого роду

4

.

Деякі властивості неперервних функцій

відрізку

,

то на цьому

;

,

Якщо функція

неперервна на

Теорема

1.

,

точка

така,

що

відрізку знайдеться хоча б одна

½

у

цій

точці буде

точка

така

що

значення

функції

.

і знайдеться хоча б одна

задовольняти) нерівності

8

у

цій

точці буде

задовольняти8 нерівності

значення)

функції

( •. 3.14).

P

на інтервалі

Тут

;

- найменше

-

найбільше, а

8

значення функції)

рис

y

M

M

m

1

m1

O

a

a

x

x2

b

b

x

1

1

1

Рис. 3.14.

129

Теорема

2.

Нехай

y

інтервалу

;

функція

неперервна на

інтервалі

і

на

кінцях

B

γ

має

значення

різних

знаків, тоді між точками

і

a

5:

точка

,

A

знайдеться

хоча

б одна

O

c

d

b

x

(рис. 3.15)5.

0

5

Рис. 3.15.

, у якій функція дорівнює

нулю

3.

Нехай

функція

визначена