
Пособие_ВМ_для_менеджеров
.pdf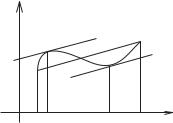
|
|
|
Теорема Лагранжа. Нехай функція |
|
|
|
|
|
|
неперервна |
|||||||||||||||||
в замкненому інтервалі |
|
|
|
, |
диференційована в усіх його |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
для якої |
||||||||
внутрішніх точках Тоді існує хоча б одна така точка |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
. |
|
|
|
|
À1, BÁ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
справедливо наступне: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
S R |
. |
|
|
|
|
|
|
|
|
|
(4.45) |
||||||
|
|
|
|
|
|
|
|
|
|
|
S R |
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Доведення: Розглянемо допоміжну функцію |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ä |
|
|
|
|
|
|
|
|
|
|
|
|
|||
і визначимо число |
|
|
так, |
щоб |
виконувалася |
|
умова |
|
|
|
|
|
|||||||||||||||
B , |
тобто щоб |
Ä1 Ä1 B ÄB. |
З цього прямує, що |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ä |
S R . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
S R |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Для функції |
|
|
|
виконуються всі умови теореми Ролля: |
||||||||||||||||||||
вона неперервна |
|
диференційована в усіх |
внутрішніх точках |
||||||||||||||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
інтервалу і приймає рівні значення на кінцях інтервалу: |
для якої |
||||||||||||||||||||||||||
|
|
. |
З цього прямує що існує хоча б одна така точка |
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
Зрозуміло що |
|
|
|
|
|
1 |
|
|||||||
виконується умова |
|
|
( |
|
|
|
. |
( |
|
|
|
|
( |
|
|
, |
|||||||||||
B |
|
( |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||
а тому |
|
|
|
|
|
|
Підставимо сюди отримане нами значення |
||||||||||||||||||||
|
|
|
. |
0 |
|
|
|
|
|
|
|
|
|
|
Ä |
|
|||||||||||
|
, |
маємо |
|
Ä 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ä |
|
|
|
|
( |
|
S R . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
S R |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отже, теорему доказано.
Формулу (4.45) називають ще
формулою кінцевих приростів
Лагранжа:
B 1 ( · B 1 .
Геометрична |
інтерпрета- |
||
|
ÅD 1, 1H |
||
ція теореми Лагранжа |
Нехай |
ÅÆ –і |
|
хорда, яка стягує точки |
: |
|
|
y |
|
|
|
|
|
M1 |
|
B |
|
|
M2 |
|
|
|
|
A |
|
|
|
|
|
|
|
|
O |
x1 ξ1 |
ξ2 |
x2 |
x |
|
|
Рис. 4.5. |
|
|
181
ÆD |
, H |
|
|
|
|
|
|
|
|
|
|
B |
B |
(см. |
рис. 4.5). А |
тому відношення |
S R |
||||||
|
|
´ |
|
S R |
|
, |
|
|
додатногоS R |
||
дорівнює тангенсу |
кута |
Ç |
нахилу хорди |
ÅÆ |
до |
||||||
напрямку осі |
|
, тобто |
|
jÇ |
|
|
|
||||
|
|
|
|
|
S R |
|
|
|
|
||
а похідна, як нам вже відомо, дорівнює тангенсу кута нахилу
j§ jÇ. |
´ |
|
|
( j§ |
|
|
|
|
||
дотичної до графіка |
функції |
в точці |
|
|
і додатним |
|||||
|
|
, тобто |
|
|
|
Звідси зрозуміло |
, |
що |
||
напрямком осі |
|
|
|
D. , H |
|
|
||||
Отже теорема Лагранжа показує, що в інтервалі |
|
|
||||||||
|
|
|
|
|
|
|
|
була б |
||
повинна знайтися точка (хоча б одна), дотична в якоїÀ1 |
, BÁ |
|||||||||
паралельна хорді ÅÆ. |
|
|
|
|
|
|
|
|
||
Приклад 4.33. Перевірити справедливість теореми |
||||||||||
Лагранжа для функції n9 |
в інтервалі |
À1, oÁ. |
|
|
|
|||||
Розв’язання: Обчислимо значення функції на кінцях
інтервалу:
1 n91 0; o n9o 1.
Знайдемо похідну функції: ( 1.
Підставимо у формулу (4.3)1 0 |
1 |
|
|
|
|
|
|
|
|
||||||
|
|
o 1 |
o 1 |
|
|
|
|
|
|
À1, oÁ |
|
||||
теорема |
|
|
|
|
|
|
|
. |
|
|
|||||
знайдемо точку |
|
|
. |
Вона належить інтервалу |
|
, |
тобто |
||||||||
|
Лагранжа для даної функції справедлива |
|
|
|
|
|
|||||||||
Теорема Коши. Нехай функції |
|
і |
|
|
неперервні в |
||||||||||
|
|
|
|
|
|
X |
|
|
|
|
в |
усіх |
його |
||
|
|
|
|
|
|
, |
диференційовані |
||||||||
замкненому інтервалі |
|
|
|
|
|
X |
|
|
|
|
|||||
внутрішніх точках, |
причому |
|
в цих точках не обертається в |
||||||||||||
|
À 1 |
, BÁ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
182 |
|
|
|
|
|
|
|
|
|
нуль. Тоді існує хоча б одна така точка , для якої справедливо наступне:
|
|
S R |
V a . |
|
(4.46) |
|
|
|
„ S „ R |
„V a |
|
|
|
випадку за |
|
XB • X1 |
|
|
|
|
Зауважимо, |
що |
. |
, |
тому що в |
протилежному |
|
заперечує |
|
|
|
X |
0 |
|
|
теоремою Ролля в розглянутому інтервалі існувала |
|||||
би точка , в якої похідна б дорівнювала нулю: |
( |
. А це |
||||
умові теореми
Доведення: Розглянемо допоміжну функцію
ÄX,
де Ä оберемо так, щоб 1 B , тобто щоб
1 ÄX1 B ÄXB .
Звідси
|
|
|
|
Ä |
S R . |
|
|
|
|
|
|
|||||
|
|
|
|
„ S „ R |
|
|
Ролля. |
|
||||||||
Функція |
|
|
задовольняє |
умовам |
теореми |
Звідси |
||||||||||
прямує, |
|
що існує така точка |
з інтервалу |
|
|
, |
для якої |
|||||||||
|
|
|
|
|
|
|
|
|
|
À: 1,( BÁ |
|
( |
||||
( |
|
|
. Продиференцюємо функцію |
|
|
|
||||||||||
|
Звідси |
|
|
|
, |
а |
|
набуває вигляду |
|
|
||||||
. 0 |
|
( ÄX( 0 |
|
Ä |
|
|
|
|
||||||||
ÄX( |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Ä |
V a . |
|
|
|
|
|
|
|
||||
|
|
|
|
„V a |
|
|
|
|
|
|
|
|
||||
Прирівняємо отримані вирази для |
Ä, маємо |
|
|
|
|
|
||||||||||
|
|
|
|
S R |
|
V a . |
|
|
|
|
|
|
||||
„ S „ R „V a
Отже, теорему доказано.
Формулу (4.46) називають формулою кінцевих приростів Коші.
183
Геометрична інтерпретація теореми Коші: Теорема Коші з геометричної точки зору має таку ж саме інтерпретацію,
що і теорема Лагранжа. Позначимо незалежну змінну через |
|
і |
|||||||||||||||||||||||||
будемо |
вважати |
що |
функції |
|
|
і |
|
|
|
є |
параметричними |
||||||||||||||||
|
|
|
|
|
|
, |
|
|
|
|
|
причому |
|
|
X |
|
|
|
|
|
|
|
|
||||
рівняннями деякої лінії |
|
|
|
|
|
|
|
|
Коли |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
змінна |
. |
точка |
||||||
параметр |
|
|
|
пробігає |
|
інтервал |
, |
|
|||||||||||||||||||
|
|
|
|
X |
|
|
|
|
|||||||||||||||||||
переміщується по лінії |
, |
початкова точка якої має координати |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
À1 |
, BÁ |
|
|
|
|
|
|
|
|||
|
1 |
|
1 |
|
, |
а |
кінцева |
|
|
B |
|
B |
|
. Кутовий коефіцієнт |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vSvR . |
|||||||||
хорди |
яка стягує ці точки |
дорівнює відношенню |
|||||||||||||||||||||||||
DX ,, |
H |
|
|
|
|
|
|
DX, |
, |
|
H |
|
|
|
|||||||||||||
Похідна від функції |
|
що задана параметрично |
|
дорівнюєS R |
|||||||||||||||||||||||
œ |
V v |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.26),„ v |
„ v |
|
||||
. Звідси формула |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
œ |
„V |
v |
|
|
|
S R |
|
V va |
|
1 ¸ ¸ B |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
„ S „ R |
„Vva , |
|
|
|
|
|
|||||||||||||||
знов описує рівність кутового коефіцієнта хорди, що стягує кінці дуги, і кутового коефіцієнта дотичної, яка проведена в деякій точці розглянутого проміжку.
4.3.2.Розкриття невизначеностей за правилом Лопіталя
Уп. 3.2 ми вже познайомилися з деякими правилами граничного переходу при розкритті невизначеностей. Познайомимося ще з одним простим і зручним прийомом обчислення границь – правилом Лопіталя. Це правило надалі ми
будемо використовувати при дослідженні функцій. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
X |
|
|
|
( |
|
. |
) одночасно прямують |
|
, |
|
|||
|
|
∞ |
|
і |
|
|
||||
|
Теорема |
Лопіталя. Нехай функції |
|
|
при |
|||||
|
|
або |
|
|
|
до нуля або |
|
до |
||
нескінченності |
Якщо відношення їх похідних має границю |
|
то |
|||||||
відношення самих функцій також має границю, яка дорівнює границі відношення похідних, тобто
lim Èa „ lim Èa „V |
(4.47) |
|
|
V . |
|
184 |
|
|

Доведення цієї теореми в загальному випадку досить
складне, тому розглянемо лише основні випадки. |
|
|
|
|
|
||||||||||||||||||||
Отже, нехай функції |
|
|
|
і |
|
|
|
|
визначенні і неперервні |
||||||||||||||||
Лопіталя |
|
|
|
|
|
|
|
|
|
при |
|
|
|
|
|
X( |
• 0 |
|
|
|
|
||||
в деякому околі точки |
|
, |
і |
|
|
X |
|
|
|
|
|
|
За теоремою |
||||||||||||
|
|
|
існують |
, |
причому |
|
|
|
|
|
. |
||||||||||||||
похідні в точці |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
lim a „ „V |
a |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
V a . |
|
|
|
|
|
|
|
|
|||||
Оскільки X 0, то |
|
|
|
|
É 2 —É 2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
a |
|
|
|
2—2a a |
. |
|
|
|
|
|
||||||||||
|
|
„ |
|
„ „ a |
|
|
Ê 2 —Ê 2a |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2—2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
||
Перейдемо до границі при |
|
|
|
|
і скористаємося теоремою про |
||||||||||||||||||||
|
|
(3.8), |
отримаємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
границю частки |
|
|
|
|
|
^_` |
|
É 2 —É 2a |
|
|
|
|
|
|
|
||||||||||
|
|
lim a „ |
|
|
, |
|
|
|
|
|
|
||||||||||||||
|
|
|
^_` |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Ê 2 —Ê 2a |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 2a |
|
2—2a |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
2—2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
за визначенням похідної остаточно маємо |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
lim a „ „V |
a |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
. |
|
|
|
|
V a . |
|
|
1, |
|
|
|
|
|
||||||||
при достатньо |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
, |
, |
|||||||
Доведемо,що ця формула справедлива и при |
|
, за |
|||||||||||||||||||||||
якщо ∞, то ¹ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
иференційовані |
||||||||||
умовою, що функції |
|
|
|
|
і |
|
|
|
визначені і д |
|
|
|
∞ |
|
|||||||||||
|
великих |
|
Зробимо заміну |
|
|
|
|
зрозуміло |
що |
||||||||||||||||
|
|
|
|
|
Маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
,RË- |
|
|
|
|
|
V,RË-·,ËRS-. |
|
|||||||||
limÈ „ limq „,R- limq „V,R-·, RS- |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ë |
|
|
|
|
|
|
|
Ë |
|
|
Ë |
|
|
|
185
Скоротимо |
отриманий вираз |
на |
1 і зробимо обернену |
||
q |
|
|
, отримаємо |
|
, qS- |
заміну 1 |
на |
|
|
||
|
|
|
limÈ „ |
limÈ „V |
|
|
|
|
|
|
V . |
Отже, для основних, найпростіших випадків теорему доведено.
Зауваження 1. Якщо відношення похідних, Èяк і відношення функції, дає невизначеність типу або È, то
правило Лопіталя, якщо в цьому є сенс, можна використовувати знов і знов до отримання результату. При повторному використанні правила Лопіталя рекомендується спочатку виконати всі можливі спрощення, наприклад, скоротити чисельник та знаменник на спільні множники або скористатися вже відомими границями.
Приклад 4.33. Обчислити границю функції
limB MASAM1B 1W.
Розв’язання:
limB MASA Ì Ì limB =SF A Ì ÌM1B 1W =S1B
limB W FW 1BA 1=.
Тут правилом Лопіталя для розкриття невизначеності необхідно було скористатися двічі.
Приклад 4.34. Обчислити границю функції
limÈ p* 1 .
Розв’язання:
186

lim È p* 1 lim È |
R lim È 1 ∞ |
||||||
|
|
|
1 |
|
. |
||
|
|
|
|
Rƒ2 |
|
|
|
Приклад 4.35. Обчислити границю функції |
|||||||
|
|
|
|
lim Sfg* S |
|
||
|
|
|
|
|
|
1 klf S. |
|
Розв’язання: |
|
|
|
|
|||
lim Sfg* S |
Ì Ì lim B ·fg* S S·B ·klf S |
|
|||||
1 klf S |
|
|
|
|
B ·fg* S |
Ì Ì |
|
lim B · fg* S S·klf S lim fg* S S·klf S |
|||||||
|
|
B ·fg* S |
|
|
fg* S |
|
|
lim B ·klf S B ·klf S S·B ·fg* S |
|
||||||
|
|
|
B ·klf S |
|
|
||
lim Bklf S Sfg* S B |
|
|
|||||
|
klf |
S |
1 |
|
|
||
|
|
|
. |
|
|
||
При обчисленні границі двічі скористалися правилом Лопіталя, попередньо двічі2скоротивши чисельник і знаменник дробі на спільний множник .
Зауваження 2. Важливо, що обчислення границь за правилом Лопіталя оправдані лише в тому випадку, якщо в результаті отримуємо кінцеву або нескінчену границю. Розглянемо приклад, коли правило Лопіталя для обчислення границь не можна застосовувати.
|
Приклад 4.36. Обчислити границю функції |
||||||
|
|
|
lim È |
|
|
|
|
|
|
|
|
|
fg* . |
|
|
|
Розв’язання: Якщо спробуємо скористатися правилом |
||||||
Лопіталя при розкритті невизначеності типу ÈÈ, отримаємо |
|||||||
lim È |
|
ÌÈÌ |
lim È |
|
V |
lim È |
1 |
|
fg* |
È |
|
fg* V |
|
1 klf , |
|
|
|
|
|
187 |
|
|
|

цей вираз при |
|
|
постійно приймає значення в інтервалі від |
||||||||||||||||||
0 до 2 (тому |
|
що |
|
|
|
), |
а тому границі немає |
Спробуємо |
|||||||||||||
|
|
∞ |
|
|
|
|
|
|
|
. |
|
3.2. |
Для |
||||||||
|
|
|
методами |
з якими познайомилися у розділі |
|||||||||||||||||
обчислити |
|
|
|
|
|
|de", |
| Â 1 |
|
|
|
|
|
|
|
|
|
|||||
цього почленно поділимо чисельник на знаменник: |
|
|
|
||||||||||||||||||
limÈ |
|
|
|
|
|
limÈ ,1 |
|
- 1 |
|
|
|
|
|
|
|
||||||
|
fg* |
|
|
|
|
|
|
fg* |
|
. |
|
|
|
|
|
|
|||||
|
Отже, границя існує і дорівнює 1. |
|
|
|
|
|
|||||||||||||||
|
Зауваження 3. За допомогою правила Лопіталя часто |
||||||||||||||||||||
вдається |
|
знайти |
границі |
|
функцій |
|
|
у |
випадках, |
крім |
вже |
||||||||||
|0 · ∞|, |
|1 |
|
|
|, |
|
|
|∞ |
|, |0 |
| |
|
|
|
і |
È , |
|
|
|
|
|||
розглянутих |
невизначеностей |
типу |
а саме |
|
|
||||||||||||||||
|
|
È |
|
|
|
|
|
|
. |
|
|
|
|
|
таких |
невизначеностей |
|||||
|
|
|
|
|
|
|
РозкриттяÌ Ì |
ÌÈÌ |
|
|
|∞ ∞|, |
||||||||||
шляхом алгебраїчних перетворень і логарифмування зводитьсяÌ Ì ÌÈÌ до розкриття невизначеностей двох основних типів: і È . Розглянемо кожну з цих ситуацій окремо.
1. Функція представлена різницею двох функцій, які
одночасно |
прямують |
до |
нескінченності |
|
(невизначеність типу |∞ ∞| . |
|
|||
|
|
|
|
|
Для обчислення такої границі за правилом Лопіталя необхідно перетворити її до вигляду дробу, чисельник і знаменник якого одночасно прямують до нуля або до нескінченності.
Приклад 4.37. Обчислити границю функції lim1 , < Y -
G1 \1 .
Розв’язання: Тут невизначеність |∞ ∞|. Приведемо різницю дробів доÌ Ì загального знаменника. Отримали
невизначеність типу , для її розкриття скористалися правилом Лопіталя двічі:
188

lim1 |
, G1 |
\1- |∞ ∞| lim1 |
G1\1 |
|
|||||||
|
< |
|
Y |
|
|
|
|
|
< \1 YD G1H |
|
|
lim1 RS \ G1 |
Ì Ì lim1 1BRRYZ<b |
Ì Ì |
|||||||||
|
<\YGB |
|
Y |
1 |
|
=<Z=<b |
|
|
|||
lim1 1=BRaABGBM |
|
|
|
|
|
||||||
|
|
B1G1AM |
Y |
|
. |
|
|
|
|
||
|
2. Функція представлена добутком нескінченно |
||||||||||
|
малої |
величини |
|
на |
нескінченно |
велику |
|||||
|
|
(невизначеність типу |™ · ∞|) |
|
|
|
||||||
Для обчислення такої границі за правилом Лопіталя необхідно її перетворити на дріб, заміняючи функцію у множнику на їй обернену. В результаті отримаємо дріб, чисельник і знаменник якого одночасно прямують до нуля або до нескінченності.
Приклад 4.38. Обчислити границю функції lim d j · n9 o .
Розв’язання: Замінимо множення на котангенс,1діленнямj на величину, обернену до котангенса. Згадаємо, що kvw ,
отриманий дріб має невизначеність типу Ì Ì. Скористаємося
правилом Лопіталя:
lim d j · n9 o |∞ · 0| lim p* z2
R {ۥ2
lim |
|
vw |
|
|
RƒÍ2 |
1 |
2 |
|
|
Ì Ì lim {|}RS2 |
|
||||||
|
p* z2 |
|
|
2ƒÍ2 |
B |
. |
|
|
3. |
|
Функція |
має |
вигляд |
степенево-показникової |
|||
|
|
(невизначеності типу: |ÎÈ|, |
¾∞™¾, ¾™™¾) |
|||||
|
|
|
|
|
|
|
|
|
Для обчислення таких границь за правилом Лопіталя необхідно спочатку функцію, яка стоїть від знаком границі,
189
прологарифмувати, знайти границю логарифма, а потім за знайденою границею логарифма знайти і границю самої функції.
|
|
|
|
R |
|
Приклад 4.39. Обчислити границю функції lim1 R—2. |
|||
|
Розв’язання: Перевіримо, чи є тут розглядувана |
|||
невизначеність. Позначимо для зручності шукану границю як Å: |
||||
lim1 |
R—2 |1È| Å. |
|
|
|
|
R |
|
|
|
|
Логарифмуємо |
дану |
границю. |
Скористаємося |
властивостями логарифмів і перетворимо отриману функцію до вигляду дробу, чисельник і знаменник якого одночасно
прямують до |
нуля при |
1. |
Скористаємося правилом |
Лопіталя: |
|
lim1 11 n9 |
|
n9Å n9 lim1 |
R—2 lim1 n9 R—2 |
||
|
R |
R |
|
lim1 1p* |
Ì Ì lim1 |
R |
|
12 1. |
|||
Знайдемо границю заданої функції, скориставшись основною |
|||||||||
властивістю логарифма, а саме: Å op*Ï |
o1 |
z1. |
|
||||||
|
4.4. ПОВЕДІНКА ФУНКЦІЇ В ІНТЕРВАЛІ |
||||||||
7, Ž |
|
|
4.4.1. Ознаки монотонності функції |
|
|||||
|
|
|
, |
|
|
|
|
|
|
|
Теорема 4.1. Для того щоб диференційована на інтервалі |
||||||||
|
функція |
|
зростала (спадала) на цьому інтервалі, |
||||||
|
|
). |
|
|
|
|
à 0 |
|
|
необхідно і |
достатньо |
щоб в усіх точках |
цього інтервалу |
||||||
( |
 0 |
|
|
|
|
( |
|
|
(недодатной |
похідна функції була невід’ємной, тобто |
|
|
|||||||
190
