
Пособие_ВМ_для_менеджеров
.pdfвказана границя називається невласним інтегралом і |
||||
позначається |
+Ô , тобто |
. |
|
|
|
+Ô |
limíÏÔ +í |
(5.49) |
|
Якщо |
вказана границя існує |
(і приймає |
скінчене |
|
значення), то невласний інтеграл називається збіжним, а якщо не існує (або прямує до нескінченності), то розбіжним.
інтеграла |
|
|
|
- |
|
|
Якщо відома первісна функція |
|
для підінтегральної |
||||
|
, то розв’язати питання |
про збіжність невласного |
||||
функції |
|
|
|
|
||
можна за формулою Ньютона Лейбниця |
|
|||||
|
+Ô |
limíÏÔ ì |
. |
(5.50) |
||
Аналогічно визначаються невласні інтеграли |
|
|||||
FÔb |
limíÏFÔ íb , limíÏFÔ ì ; 5.51) |
|||||
FÔÔ |
FÔD DÔ |
∞ f f ∞ . |
(5.52) |
|||
З (5.52) зрозуміло, що якщо кожен з невласних інтегралів праворуч збігається, то збігається й невласний інтеграл праворуч.
|
Приклад 5.43. Обчислити невласний інтеграл (або |
||||
встановити його розбіжність) Ô |
√@<<. |
||||
√< |
Розв’язання: За формулою (5.50) маємо |
||||
limíÏÔ 2√ % |
ì |
G |
2 lim &ì 2√1 ∞ 2 ∞ |
||
Ô @< |
|
|
íÏÔ |
, |
|
|
|
1 |
|
|
|
отже, даний невласний інтеграл розбігається.
Приклад 5.44. ОбчислитиÔ · F<невласний? інтеграл (або встановити його розбіжність) t .
271
|
|
Розв’язання: Зробимо заміну змінної та скористаємося |
|||||||||||||||||||||||||
формулою (5.51): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Ô |
|
F<? |
|
|
X |
|
|
|
Y |
|
FÔ |
|
|
|
|
|
t |
|
|
||||||||
t · |
|
|
|
|
н |
|
0 |
|
|
t |
|
|
|
FÔ |
|
||||||||||||
|
|
|
|
|
|
0 |
G |
|
в |
|
∞ |
|
|
í |
|
|
|
|
, |
|
|
|
|
|
|||
lim |
„ |
|
t |
|
|
lim |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ì |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
íÏFÔ |
|
|
|
|
|
|
|
|
|
|
íÏFÔ |
|
|
|
|
|
|
|
|
|
|
|
||||
Тобто даний невласний інтеграл збігається і дорівнює . |
|
||||||||||||||||||||||||||
|
5.14.2. Невласні інтеграли від розривних функцій |
||||||||||||||||||||||||||
|
|
Визначення 5.6. Нехай функція |
|
|
|
визначена і |
|||||||||||||||||||||
неперервна на інтервалі |
|
|
|
а в точці |
|
|
|
|
функція або не |
||||||||||||||||||
визначена |
, |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||
або має розрив другого роду |
|
|
В цьому випадку не |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G G |
|
|
. |
|
|
, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
), , |
|
|
|
|
|
|
|
|
|||||
можна говорити про визначний інтеграл (за визначенням він є
границею інтегральних сум), бо функція |
|
, |
|
|
не є неперервною |
||||||||||||
|
|
|
, тому границя може |
не існувати |
. |
Позначимо |
|||||||||||
на інтервалі |
|
|
|
|
|
|
|||||||||||
|
|
функції |
яка має розрив в точці |
|
|
, |
так |
|
|
|
|
||||||
інтеграл від |
|
), ,* , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
+b |
limîÏt +bFî . |
|
|
|
(5.53) |
|||||||||
|
|
|
|
|
|
), , |
|
|
|
|
|
|
|
|
|||
Якщо |
існує |
|
ця границя |
(5.53), то функція |
|
|
|
називається |
|||||||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
вказана границя |
||||
інтегровною невласно на проміжку |
|
|
|
|
|
а |
|
|
|
|
|||||||
називається невласним інтегралом . |
|
|
G G |
|
|
|
|
|
|
||||||||
|
Аналогічно визначається невласний інтеграл, якщо |
||||||||||||||||
функція має розрив на нижній границі : |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
+b |
limîÏt +b î . |
|
|
(5.54) |
||||||||||
|
|
|
|
272 |
|
|
|
|
|
|
|
|
|
|
), ,* |
|
|
|
В тому випадку, якщо функція |
|
|
|
|
має розрив в деякій |
|||||||||||
|
|
, |
|
|
|
|
|
інтегрування |
, |
то |
|||||||
точці |
|
яка належить інтервалу |
|
|
|
|
|
|
|
||||||||

інтеграл розбивають на два, в одному з них функція має розрив на верхній границі (5.53), а в другому – на нижній (5.54):
|
+b |
+D Db . |
|
(5.55) |
|||
Приклад 5.45. |
Обчислити |
невласний інтеграл |
(або |
||||
встановити його розбіжність) |
t |
W√ 5F< |
|
|
|||
5 |
@< . |
|
|
||||
Розв’язання: Функція має розрив на верхній границі, в |
|||||||
точці |
, при знаходженні первісної, виконаємо заміну |
||||||
змінної. |
Перепишемо інтеграл |
за |
властивістю |
(5.38), |
точка |
||
16 |
|
|
|
|
|
||
розриву опинилася на нижній границі, тому скористаємося
формулою (5.54): |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ƒ |
|
|
|||||||||
5 W @< |
|
|
X н |
|
|
|
16Y |
|
|
t |
W@ |
|
|
5 |
|
FW |
|
|
|||||||||
t |
√ 5F< |
|
|
16 0 |
|
5 |
√ |
|
t |
|
|
||||||||||||||||
|
|
|
C |
|
в |
|
16 16 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
W |
|
16 |
|
; |
W |
|
|
|
; |
|
|
W |
|
|
|
|
|
|
|
|
4 |
4 , |
||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
ï |
|
|
||||||||||||
|
|
W |
« 0 ï |
|
4 |
√16 |
4 lim |
|
& 0 |
|
|
4 |
0 |
4 |
|||||||||||||
|
|
îÏt GC |
|
|
|
|
|
|
|
4 |
|
|
îÏt |
|
|
|
|
|
|
4 |
|
|
|
|
|
||
отже невласний інтеграл збігається і дорівнює 44 . |
|
|
|
(або |
|||||||||||||||||||||||
|
|
Приклад 5.46. |
|
Обчислити |
невласний |
інтеграл |
|||||||||||||||||||||
встановити його розбіжність) |
t <?F;< 4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
@< . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Розв’язання: Функція має точку розриву в середині |
|||||||||||||||||||||||||
інтервалу інтегрування, а саме в точці |
|
|
|
|
|
. Розіб’ємо інтеграл |
|||||||||||||||||||||
на два (5.55). Дослідимо |
|
|
|
|
отриманих |
інтегралів на |
|||||||||||||||||||||
кожен |
з |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
збіжність за формулами (5.53), (5.54): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
@< |
|
|
|
@< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t |
<?F;< 4 |
|
t |
<F ?F |
|
|
G |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
|
lim |
îÏt |
j |
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|||||
|
|
%<F %„ |
|
|
|
%<F %„ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
<F F |
1 ï |
|
<F F |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
273 |
|
|
|
|
|
1 ï |
|
|
|
|
|
|
|||
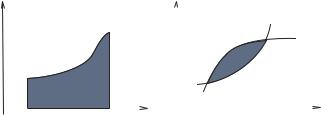
∞ 3. |
1 ∞ |
∞ |
отже, невласний інтеграл |
|
|
, |
|
розбігається |
|
|
|
5.15. ДЕЯКІ ГЕОМЕТРИЧНІ ЗАСТОСУВАННЯ ВИЗНАЧЕНИХ ІНТЕГРАЛІВ
5.15.1. Обчислення площі плоскої фігури
За |
Õ |
геометричним |
тлумаченням |
визначного інтегралу |
||||||||
|
|
|
|
|
|
|
, |
|
|
Ö |
|
|
(5.31), площа криволінійної трапеції (рис. 5.7,а), |
яка обмежена |
|||||||||||
кривою |
|
, лініями |
|
|
і |
|
|
, |
і віссю |
|
, |
|
обчислюється за формулою |
+ |
|
|
|
|
|
|
|
||||
|
|
Ë |
|
. |
|
|
|
(5.56) |
||||
|
|
|
|
b |
|
|
|
|
|
|||
Якщо плоска фігура обмежена лініями Õ і
(рис. 5.7,б), то для обчислення площі, , необхідно знайти точки перетину кривих і . Ці точки є
границями інтегрування.
|
y |
|
|
y=f(x) |
|
|
|
y |
|
|
|
|
|
y=f(x) |
||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=f(x) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
x |
|
|
|
|
|
a |
|
|
|
x |
|||
O |
b |
|
O |
(б) |
b |
|||||||||||||
|
(а) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
Рис. 5.7. |
|
|
|
|
|
|
|
|||||
|
Шукана площа плоскої фігури може бути знайдена як |
|||||||||||||||||
, ,, |
Õ , Õ |
0, |
|
, , |
|
|
Õ |
, Õ 0, |
||||||||||
різниця між площами криволінійних трапецій, |
обмежених |
|||||||||||||||||
лініями |
|
|
|
|
|
|
|
|
|
|
|
і |
|
|
|
|
|
|
|
|
тобто |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
274 |
|
|
|
|
|
|
|
|
|
|||

|
|
|
|
|
|
b |
|
|
|
b |
|
|
|
|
b |
|
|
* |
|
. |
|||
Ë |
|
|
+ |
|
|
+ |
|
+ ) |
|
|
|||||||||||||
|
Ë Ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.57) |
|
|
|
Приклад 5.47. Обчислити площу фігури, обмеженої |
|||||||||||||||||||||
лініями |
Õ |
|
|
і |
Õ |
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Розв’язання: Побудуємо |
фігуру |
|
|
y |
|
|
|
||||||||||||||
(рис. 5.8). Знайдемо точки перетину |
|
|
|
|
|
|
|||||||||||||||||
кривих, для цього розв’яжемо систему |
|
|
|
|
|
|
|||||||||||||||||
рівнянь |
|
|
|
|
|
|
|
2; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Õ |
|
|
; |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
ð |
|
|
G |
|
|
|
|
|
2 |
|
|
0; |
|
|
|
|
|
O |
2 |
|
x |
||
|
2 |
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|||||||||
Õ |
|
|
|
|
|
|
1; |
|
2. |
|
|
|
Рис. 5.8. |
|
|
||||||||
Отже, точки перетину |
1 і |
|
|
|
|
|
|
|
|
||||||||||||||
Ë |
|
|
Обчислимо площу за формулою (5.57): |
|
|
|
|
||||||||||||
b |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
G |
+ ) |
4 |
|
|
* |
|
F |
2 4 |
|
4 |
од |
|
|
||||||
- |
2 |
.% 1 |
2 4 4 |
|
|
||||||||||||||
|
<? |
|
|
<C |
2 |
|
|
|
|
7 |
|
|
|
|
. |
|
|||
|
|
|
5.15.2. Обчислення довжини дуги плоскої кривої |
|
|||||||||||||||
ó цієї кривої, яка |
Õ |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
p” |
|
Нехай |
в |
|
декартовій |
системі |
|
координат |
задано |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||
неперервну криву |
|
|
|
|
(рис. 5.9). Знайдемо довжину дуги |
||||||||||||||
|
|
|
|
|
|
розташована в інтервалі між |
|
і |
|
|
|||||||||
275

y |
|
|
|
|
Mi-1 |
Mi |
B y=f(x) |
|||
|
|
|
|
|
|
yi |
|
|
||
|
|
|
M2 |
|
xi |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
a=x0 |
|
x1 |
|
|
|
x2 |
|
|
|
|
|
|
xi-1 xi |
b=xn |
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p” |
|
|
|
Рис. 5.9. |
|
|
|
|
|
|
|
||||||
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
É , É , … , É , … |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ó |
|
точками |
|
|
|
|
> |
з абсцисами |
||||||||||
|
Поділимо дугу |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
pÉ , É É , … ,.É F |
” |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||
∆ , ∆ , …в, ∆ |
|
|
|
|
|
. |
|
Поєднаємо |
|
|
|
|
точки |
|
|
відрізками |
|||||||||||||||
, , … , >, … |
|
p” |
|
, |
|
довжини |
яких |
позначимо |
|
відповідно |
|||||||||||||||||||||
|
|
∆ > |
|
|
|
Ми отримали |
ламану |
|
|
|
|
|
яка |
||||||||||||||||||
|
|
|
|
|
ó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вписана |
дугу |
|
|
|
|
Довжина |
ламаної |
складається з довжин |
|||||||||||||||||||||||
відрізків |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑>I |
∆ >. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Довжиною |
дуги |
p” |
називають границю, до якої прямує |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
довжина ламаної, |
|
|
|
|
|
|
|
прямуванні її найбільшого відрізка до |
|||||||||||||||||||||||
|
при |
|
|
ó |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
нуля, а числа відрізків |
Ï ∞: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim~+<∆[ÓÏt, ÏÔ ∑>I ∆ >. |
|
|
|
(5.58) |
||||||||||||||||
як ∆Õ> |
Визначимо спосіб обчислення довжини дуги. |
|
|
|
|||||||||||||||||||||||||||
|
> |
|
>F . За теоремою Піфагора |
|
|
|
|
||||||||||||||||||||||||
|
Позначимо різниці ординат двох сусідніх точок ділення |
||||||||||||||||||||||||||||||
|
|
∆ & ∆ |
|
∆Õ |
|
|
|
1 -∆< |
. ∆ |
|
|
|
|||||||||||||||||||
|
|
|
|
> |
|
|
|
|
|
|
|
> |
|
|
|
|
|
|
> |
|
|
Å |
|
∆ôÓ |
|
> |
. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ó |
|
|
|
|
|||||||||
За теоремою Лагранжа маємо |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
∆ôÓ |
|
|
Ú <Ó |
FÚ <ÓZƒ |
|
|
, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
∆<Ó |
|
|
|
|
|
<ÓF<ÓZƒ |
|
|
Í> |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
276 |
|
|
|
|
|
|
|
|
|
||

де >F f Í> f >.
Звідси довжина часткового відрізку ламаної дорівнює
∆ |
Å |
1 A |
Í |
B ∆ |
|
> |
|
> |
|
> |
|
|
|
||||
Знайдемо границю інтегральної суми, яка дорівнює визначеному інтегралу
lim ÏÔ |
|
∑ |
|
1 A |
Í B |
|
∆ |
+ |
Å |
1 A |
B |
|
|
|||||
~+<∆[ÓÏt |
|
|
|
|
|
|
> |
> |
|
b |
|
|
|
|
. |
|||
|
>I Å |
|
|
|
|
|
|
|
|
|
|
|
||||||
Остаточно формула для обчислення довжини дуги має |
||||||||||||||||||
вигляд: |
|
|
|
|
+b Å1 A B . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(5.59) |
||||||||||
розташована між |
0 |
і |
|
. |
|
|
|
|
Õ |
|
1 |
|
||||||
Приклад |
|
|
|
|
|
|
|
|
|
|
|
|
, яка |
|||||
5.48. |
Знайти довжину лінії |
|
|
|
|
|
||||||||||||
Розв’язання: |
|
Для |
|
обчислення |
|
|
довжини |
|
дуги, |
|||||||||
скористаємося формулою (5.59). До підстановки у формулу виконаємо попередні обчислення, а саме
Õ |
|
F<< ? |
; |
|
;<? |
|
F <? <W ;<? |
<? <W |
A <?B?; |
||||||||
1 Õ |
|
|
|
1 |
|
||||||||||||
|
|
|
F<? ? |
F<? ? |
|
ƒ |
F<? ? |
F<? ? |
|||||||||
|
b |
&1 Õ |
ƒ |
<? |
|
|
FA F<?B |
|
|
||||||||
+ |
t? |
F<? |
t? |
F<? |
|
|
|||||||||||
|
ƒ |
@< |
|
|
|
ƒ |
|
G |
<F |
1⁄2 |
|
1⁄2 |
G |
|
|
||
|
? |
? |
|
|
? |
|
|
|
|||||||||
|
2 t |
F< |
t |
|
|
0 |
|
% 0 |
4 |
||||||||
|
|
%< %„ |
|
|
|||||||||||||
|
3 |
од. |
|
|
277 |
|
|
|
|
|
|
||||||
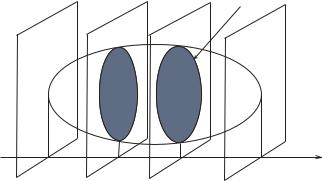
5.15.3. Обчислення об’єму тіла
Нехай дано тіло, яке обмежено замкненою поверхнею, і нехай відома площаÖ будь-якого його перетину площиною, паралельною осі (рис. 5.10).
БудемоËвважати, що площа такого перетину є відомою нам функцією .
S(xi )
a xi-1 xi b x
Рис. 5.10.
Нехай все тіло обмежене двома площинами,
перпендикулярними |
|
до |
осі |
|
|
і |
|
відомо, |
|
що ці |
площини |
|||||
|
|
|
|
|
точках |
|
|
|
|
|
. |
Для визначення |
||||
перетинають вісь |
|
|
в |
на |
|
Ö |
за |
|
|
|
|
|
||||
об’єму разіб’ємо |
тіло |
шари |
допомогою площин які |
|||||||||||||
Ö |
|
|
|
|
|
|
|
, |
, |
|
|
|
, |
|||
, , … , >, … |
|
|
, |
|
|
|
|
|
|
|
. |
’ |
|
|
|
|
перпендикулярні |
осі |
|
|
і перетинають |
|
вісь |
в точках |
|||||||||
|
|
|
|
|
кожен шар прямим циліндром тієї ж |
|||||||||||
|
ЗамінимоÖ |
|
|
|
|
|
|
|
|
|
|
|
||||
висоти і з основою |
|
яка дорівнює |
|
|
Об єм прямокутного |
|||||||||||
|
|
|
|
|
|
|
|
|
основи на висоту Отже об єм |
|||||||
циліндру дорівнює добутку площі |
|
Ë > |
|
|
|
. |
’ |
|||||||||
-ступінчатого тіла знаходиться як сума |
|
|
|
|
|
|||||||||||
|
|
|
|
õ |
∑>IE |
Ë> ∆>. |
|
|
|
|
(5.60) |
|||||
Об’ємом тіла називається границя інтегральної суми при |
||||||||||||||||
|
|
|
|
|
відрізку до нуля а числа |
Ï ∞: |
||||||||||
прямуванні найбільшого |
|
|
278 |
|
|
, |
|
|
|
|||||||
|
|
õ |
|
lim~+<∆<ÓÏt ∑>IE |
Ë> ∆> |
+b Ë. |
(5.61) |
|||
|
|
|
|
|
ÏÔ |
|
|
|
|
|
Õ |
Якщо |
тіло, |
об’єм якого ми |
шукаємо, |
отримане |
|||||
|
|
|
|
, |
Ö |
|
|
|
|
|
обертанням |
криволінійної трапеції, яка обмежена лінією |
|||||||||
|
|
|
навколо осі |
|
, то перпендикулярним перетином з |
|||||
|
Õ |
|
|
|
|
|
|
|||
абсцисою |
|
є коло радіус якого дорівнює відповідній ординаті |
||||||||
лінії |
|
|
|
. В такому разі |
´ · Õ . |
|
|
|||
|
|
|
|
|
|
Ë |
|
|
||
Звідси отримаємо формулу для обчислення об’єму тіла обертання:
|
|
|
|
|
|
|
|
|
õ |
|
´ +b Õ |
´ +b . |
(5.62) |
|||||||||
|
|
|
Приклад 5.49. Знайти об’єм тіла обертання фігури, |
|||||||||||||||||||
обмеженої лініями |
Õ |
|
4 |
, Õ |
|
4 |
навколо осі Ö, де • 0. |
|||||||||||||||
|
|
|
Розв’язання: Знайдемо точки перетину ліній, які |
|||||||||||||||||||
обмежують цю фігуру: |
|
4 4 |
0 |
|
|
|
|
|||||||||||||||
|
Õ |
|
4 |
; |
|
|
4 |
|
|
4 ; |
|
|
|
|
|
|||||||
ð |
|
G |
|
|
|
|
4 |
|
0; |
|
|
|
|
|
|
|
||||||
Õ |
4 |
|
|
|
|
|
|
4 |
2. |
|
|
|
||||||||||
|
|
|
|
|
|
0; |
|
|
2; |
|
|
|
||||||||||
|
|
|
За формулою (5.62) маємо |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
t ) |
|
|
|
|
|
* |
|
|
|
t |
|
|
|
||||||
õ |
|
|
|
|
|
|
|
|
|
16 |
|
|||||||||||
´ |
|
Õ |
|
Õ |
|
|
|
|
´ |
|
||||||||||||
|
|
|
5<C |
<ö |
2 |
|
|
7 7 |
0 |
|
4 . |
|
||||||||||
|
|
G |
4 |
|
9 .% 0 |
|
´ - 4 |
|
|
9 . ´ од |
|
|||||||||||
|
|
´ - |
|
|
|
|
||||||||||||||||
279

5.16. Застосування визначних інтегралів для розв’язанні задач економіки
Познайомимося з основними поняттями, необхідними
нам для розв’язання задач економіки. |
|
|
|
|
|||
Нехай функція |
|
|
описує |
продуктивність |
|||
деякого виробництва за певний час |
Об |
єм продукції |
, |
||||
|
|
• |
. |
’ |
|
|
|
яка вироблена за проміжок часу |
)" , " *, |
обчислюється за |
|||||
формулою |
• " , " |
KKƒ? |
|
• " , " |
|||
|
" ". |
|
(5.63) |
||||
На продуктивність виробництва продукції може впливати багато різних факторів. Можливість урахування цих
факторів, пов’язана з використанням функцій Кобба-Дугласа. В |
||||||||||||||||||||||||
такому випадку функція " є добутком трьох множників |
|
|
|
|||||||||||||||||||||
|
p " , ÷ " , ø " |
" |
tp… " ÷Š " øù " , |
|
|
|
(5.64) |
|||||||||||||||||
|
- |
|
t, Œ, ’, ú |
|
|
|
|
|
|
|
|
|
|
|||||||||||
де |
|
|
|
|
|
|
величини затрат природних ресурсів, праці |
|||||||||||||||||
і капіталу (відповідно), |
|
|
|
|
|
|
- деякі коефіцієнти. |
|
|
|
|
|||||||||||||
Õ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Нехай |
|
дано |
|
|
функцію |
|
y |
|
|
|
A |
|
|
|
|
||||||||
|
|
, |
|
|
яка |
|
характеризує |
1 |
|
|
|
|
|
|
|
|||||||||
нерівномірність розподілу доходів |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
серед населення, де |
|
|
- |
частинка |
|
|
y=x |
|
|
|
|
|
|
|
||||||||||
сукупного |
доходу, |
|
яку |
отримує |
|
|
|
B |
|
|
|
|
|
|||||||||||
|
Õ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
частинка |
|
|
|
|
|
|
найбіднішого |
|
|
|
|
|
|
|
|
|
|
|||||||
населення. |
Графік |
|
цієї функції |
|
|
y=f(x) |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
Лоренца |
|
|
C |
|
|
|
|||||||||||
називається |
|
кривою |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Î, |
|
|
|
Ý )0; 1* |
|
|
|
|
|
|
|
|
|
1 |
|
, |
x |
|||||||
(рис. 5.11). |
Очевидно, |
, |
що |
|
|
|
|
|
Рис. 5.11. |
|
|
|||||||||||||
|
|
|
при |
|
|
|
|
|
а з |
цього |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
0 Î |
|
|
|
|
|
|
|
|
|
|
||||
прямує що нерівномірність розподілу доходів тим більша |
|
чим |
||||||||||||||||||||||
більша площа |
фігури |
|
|
|
|
. |
Тому для кількісного аналізу |
|||||||||||||||||
|
c |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
Öp” |
|
|
|
|
||
|
|
|
|
|
|
розподілу доходів використовують |
коефіцієнт |
|||||||||||||||||
нерівномірності |
|
|
|
|
|
Öp” |
|
280 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Öp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Джині , який дорівнює відношенню площі фігури |
|
|
|
і площі |
||||||||||||||||||||
трикутника
