Джерела нагрівання та

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Так само як і в попередньому випадку, співвідношення коефіцієнтів у правій частині цього рівняння виділимо в окрему фізичну величину. По-

Інтегруємо це рівняння відповідно до правил інтегрування, одержимо:

ln( T − TC ) = −bC t + C

Постійну інтегрування C знайдемо з початкових умов (б): при t = 0 , T =Tпоч , тоді постійна інтегрування буде: ln( Tпоч −TC ) = С

Отже, кінцеве рівняння охолодження стержня в повітрі буде:

ln ( T −TС ) = −bС t + ln ( Tпоч −TС )

Після потенціювання (антилогарифм) отримаємо рівняння, яке описує процес вільного охолодження циліндричного стержня в повітрі:

T −TС =( Tпоч −TС )e−bС t

Нагадаємо, що тут:

Tпоч − початкова температура стержня (в момент часу t =0 );

TC − температура оточуючого середовища;

bC − коефіцієнт температуровіддачі поверхні стержня [с − 1], обчислю-

ється із залежності: bС = 4α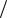(cρD),

де: α − коефіцієнт повної поверхневої тепловіддачі; cρ − об’ємна теплоємність матеріалу стержня;

D − діаметр стержня

191

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

ПРИКЛАДИ АНАЛІТИЧНИХ РІШЕНЬ ДИФЕРЕНЦІЙНОГО

РІВНЯННЯ ТЕПЛОПРОВІДНОСТІ

Миттєве точкове джерело тепла в необмеженому тілі

Нехай в деякій точці необмеженого тіла, яку сумістимо з початком координат (O ) (див. рис.) миттєво виділяється деяка кінцева (і відома) кількість теплоти Q , [Дж]; Необхідно знайти приріст температури, який ви-

кличе ця виділена теплота в деякій точці A з відомими відносно джерела тепла координатами ( x, y,z ) через деякий час t після того, як виділилось тепло в точці O . При цьому відомо, що роз-

повсюдження теплоти в тілі описується диференційним рівнянням теплопровідності:

всі складові цього рівняння були докладно описані вище. Приймемо також наступні передумови:

−джерело тепла нерухоме, час його дії tд нескінченно малий tд → 0 ,

але час розповсюдження теплоти в тілі − необмежений: t → ∞ ;

−тіло нескінченне і анізотропне (всі властивості в усі сторони однакові);

−теплообміну на границях тіла немає, тобто він не впливає на теплопередачу в тілі;

−початкова температура всіх точок тіла однакова і відома T0 ;

−теплофізичні коефіцієнти λ, cρ, a ) не залежать від температури

λ, cρ, a = const .

Вирішити диференційне рівняння − це означає знайти таку функцію (для даного випадку залежність температури від змінних параметрів

192

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

x, y, z, t ): T = f (x, y, z, t ), частинні похідні якої другого порядку по осях координат x, y, z ; і першого порядку по часу t після підстановки у дифе-

ренційне рівняння забезпечать рівність його лівої і правої частин.

Таку функцію справді можливо віднайти (Д. Розенталь, М.М. Рикалін) і при виконанні всіх наведених вище передумов і при умові суміщення початку координат з точкою дії миттєвого джерела тепла, рішенням диференційного рівняння теплопровідності буде залежність:

a - температуропровідність: a = λ ; cr

t - час, який обчислюється з моменту виділення тепла;

R - радіус-вектор точки, для якої знаходиться температура,

відносно точки виділення тепла: R2 = x2 + y2 + z2 .

Доводиться справедливість залежності (М1) для описаного випадку методом від противного: беруться похідні другого порядку по осях координат x , y ,z і похідна першого порядку по часу t , після чого отримані за-

лежності підставляються в диференційне рівняння теплопровідності і ви-

являється, що його ліва частина не суперечить правій - вони рівні. Математично це процедура досить громіздка, але всякий, хто її виконає, може пересвідчитись в правильності.

Таким чином, залежність (М1) описує температурне поле в необмеженому тілі при дії в ньому миттєвого точкового джерела тепла.

193

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Дослідимо її:

Права частина рівняння (М1) є добуток двох співмножників:

перший співмножник характеризує температуру в точці внесення теп-

іншому напрямку, в деякі фіксовані моменти часу t =const , являють поді-

бні між собою плавно затухаючі криві, нахил яких поступово зменшується із збільшенням часу t (див. рис. нижче, а).

Термічні цикли T = f (t ) при x, y,z = const відповідають фізичній мо-

делі процесу: температури точок тіла спочатку швидко зростають, потім плавно спадають (див. рис. нижче, б).

Термічні цикли являють собою експоненціальні криві з чітко вираженим максимумом.

Максимальні температури

Максимальний приріст температури Tm в деякій точці тіла з заданим

194

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

відносно джерела тепла радіусом-вектором R і час настання цієї максимальної температури tm (див. рис. нижче, б) можна знайти відповідно до правил визначення екстремуму функції: похідна в точці екстремуму повинна дорівнювати нулю.

Візьмемо похідну по часі ∂T 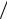∂t залежності (М1) і прирівняємо її до нуля не забуваючи, що вираз (М1) є добуток двох функцій. Позначимо їх:

після винесення за дужки подібних елементів буде:

Неважко бачити, що вираз у фігурних дужках є не що інше, як само рівняння (М1), тобто значення приросту температури. Тепер поза дужки винесемо ще й вираз 1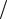t , тоді пошукувана похідна буде:

В точці екстремуму похідна повинна бути рівна нулю. Останній, щой-

но отриманий, вираз похідної може бути рівний нулю ( ∂( T ) = 0 ) при од-

¶t

ній з трьох умов:

195

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

1)T = 0 - означає, що теплота в тілі не розповсюджується - це не відповідає дійсній початковій умові і тому повинно бути відкинуто;

2)t → ∞ − означає, що все тепло уже рівномірно розповсюдилось в тілі − це теж не відповідає дійсній початковій умові і теж повинно бути відкинуто;

3)R2 − 3 = 0 − для означених умов має фізичний зміст і тому пови- 4at 2

нно бути проаналізовано докладніше, як єдине дійсне для точки екстремуму.

З рівності (3) тепер можна знайти час настання максимальної темпе- ратури при дії миттєвого точкового джерела тепла в необмеженому тілі:

tm = R2

6a

Підставляючи цей вираз часу настання максимуму в залежність (М1) знайдемо й відповідний йому максимальний досягнутий термічним циклом в точці з радіусом-вектором відносно джерела тепла R приріст температури:

x, y,z - координати точки відносно джерела тепла;

е – основа натуральних логарифмів, е » 2,718282.

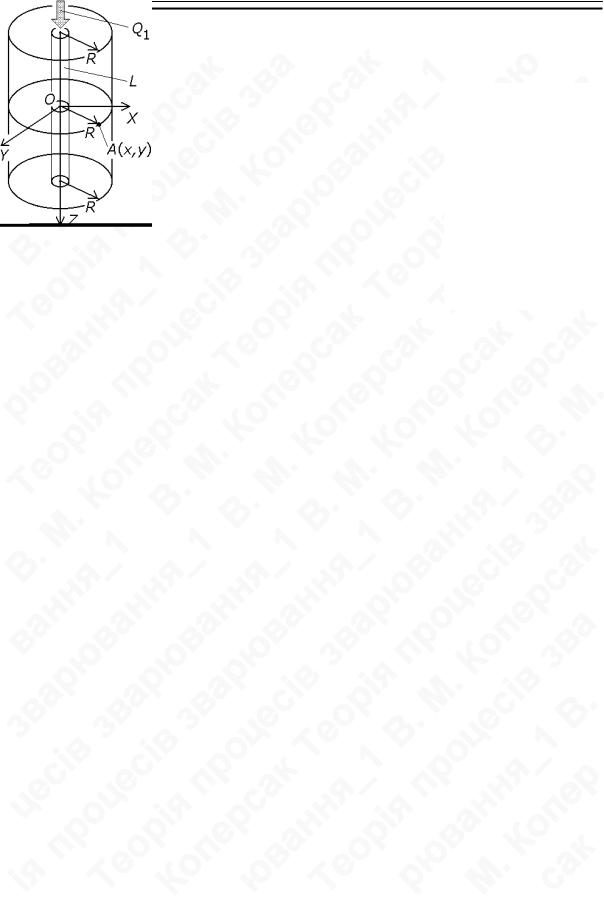
Миттєве лінійне джерело тепла в необмеженому тілі

Нехай в необмеженому тілі вздовж деякої лінії L (див. рис. нижче) миттєво виділяється деяка кількість теплоти. Лінія ця нескінчена, як і тіло, і кількість теплоти, яка виділяється вздовж неї виходить теж нескінченно велика, але будемо вважати відомим, що на кожній одиниці довжини цієї лінії виділяється деяка кінцева кількість теплоти. Назвемо цю величину ін-

196

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

тенсивність тепловиділення і позначимо Q1 , [Дж/м]. Відповідно, для умов необмеженого тіла буде:

де: Q − загальна кількість теплоти, яка миттєво виділяється вздовж лінії L ;

L − довжина лінії тепловиділення.

Таким чином, тепловкладення в одиницю довжини лінії джерела тепла є величина постійна: Q1 = const і

будемо вважати цю величину відомою: Q1 .

Необхідно знайти приріст температури, який викличе ця виділена теплота, інтенсивністю Q1 , в деякій точці A з відомими відносно джерела тепла координатами ( x, y ) через деякий час t після того, як виділилось те-

пло вздовж лінії L .

Для початку розташуємо координатні осі таким чином, щоб вісь OZ співпадала з лінією виділення тепла L , а координатна площина XOY захоплювала точку A , для якої знаходиться температура. Це дасть змогу використати частинний випадок диференційного рівняння теплопровідності

всі складові цього рівняння були докладно описані вище. Приймемо також подібні до попереднього наступні передумови:

197

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

−джерело тепла (лінія) нерухоме, час його дії tд нескінченно малий: tд ® 0 , але час розповсюдження теплоти в тілі − необ-

межений: t → ∞ ;

−тіло нескінченне і анізотропне (всі властивості в усі сторони однакові);

−теплообміну на границях тіла немає, тобто він не впливає на теплопередачу в тілі;

−початкова температура всіх точок тіла однакова і відома T0 ;

−теплофізичні властивості матеріалу тіла ( λ, cρ, a ) не залежать

від температури ( λ, cρ, a = const ).

Вирішити диференційне рівняння – означає знайти таку функцію (залежність температури від змінних параметрів): T = f (x, y, z, t ), частинні похідні якої, другого порядку по осях координат x, y і першого порядку по часу t , після підстановки у диференційне рівняння забезпечать рівність його лівої і правої частин. (Вісь z співпадає з лінією тепловиділення L і через це від значення координати z приріст температури не залежить: паралельно лінії L на рівних відстанях від неї температури (прирости температур) однакові.

Таку залежність теж було встановлено свого часу і при виконанні всіх наведених вище передумов та ще й при умові суміщення початку координат з лінією дії миттєвого джерела тепла, рішення диференційного рівняння теплопровідності в площині XOY для даного випадку буде мати ви-

198

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

a − температуропровідність: a = λ , тут λ − теплопровідність;

сρ

t − час, який обчислюється з моменту виділення тепла;

R − радіус-вектор точки, для якої знаходиться температура відно-

сно лінії виділення тепла: R2 = x2 + y 2

Доводиться справедливість залежності (М2) для описаного випадку методом від противного: беруться похідні другого порядку по осях координат і похідна першого порядку по часу t , після чого отримані залежності підставляються в диференційне рівняння теплопровідності (в його частковий випадок для плоского температурного поля) і виявляється, що його лі-

ва частина не суперечить правій − вони рівні.

Таким чином, залежність (М2) описує температурне поле в необмеженому тілі при дії в ньому миттєвого лінійного джерела тепла. Дослідимо її:

Права частина рівняння є добуток двох співмножників:

перший співмножник характеризує температуру в лінії внесення тепла L :

температури від відстані до лінії внесення тепла.

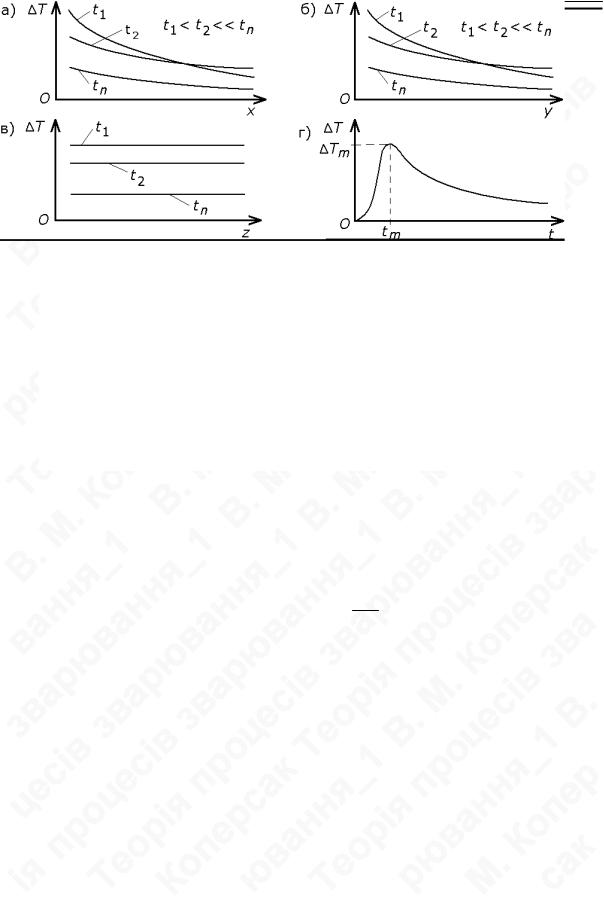
Ізотерми такого температурного поля являють собою циліндричні поверхні з осьовою лінією OZ (L).

Ізохрони ( T = f (x) або T = f (y)) в деякі фіксовані моменти часу

( t = const ) являють собою плавно затухаючі криві, нахил яких поступово зменшується із збільшенням часу t (див. рис. нижче: (а, б)). Ізохрони по напрямках, паралельних осі OZ , являють собою горизонтальні лінії (див. там же, (в)). На однакових відстанях від осі OZ температури однакові для

199

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

будь-якого моменту часу, що витікає із самої суті початкових передумов: лінія джерела тепла співпадає з віссю OZ .

Термічні цикли ( T = f (t ) при x, y = const ) див. на рисунку нижче (г).

Максимальну температуру термічного циклу та час її настання знаходять аналогічно до попереднього з умови екстремуму – рівність нулю по-

хідної в точці екстремуму: ∂T 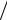∂t = 0 .

Виконавши з рівнянням (М2) дії, аналогічні описаним у попередньому випадку для миттєвого точкового джерела тепла, отримаємо значення часу настання максимальної температури у випадку дії миттєвого лінійного

джерела тепла в необмеженому тілі: tm = R2

4a

Підставляючи це значення часу в рівняння (М2) отримаємо максимальний приріст температури в заданій точці A(x, y):

е – основа натуральних логарифмів, е » 2,718282.

200