Джерела нагрівання та

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

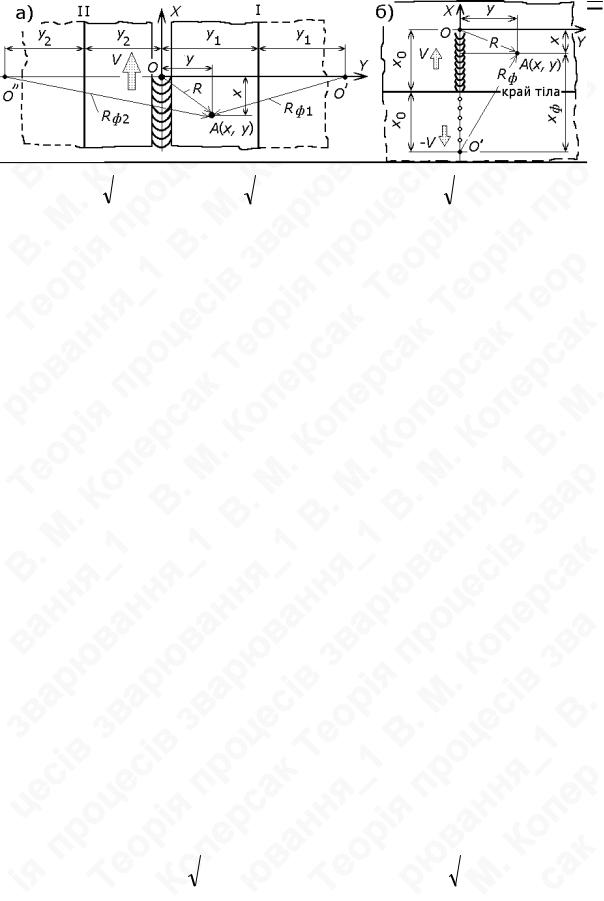
ється надто близько до обмежуючої поверхні (до краю зварюваного виробу). Оскільки зварювання ведеться найчастіше в повітрі і гранична поверхня контактує з повітрям, а теплопровідність повітря набагато менша ніж теплопровідність будь-якого металу, то граничну поверхню в більшості випадків вважають адіабатичною. Таке припущення недалеке від реальності і, крім того, його легко врахувати, добудовуючи тіла до необмежених, вводячи симетрично граничній поверхні фіктивні джерела тепла і користуючись потім принципом накладення (суперпозиції). Якщо ця умова непридатна, тоді доводиться або задавати величину теплового потоку через граничну поверхню, або задавати її температуру, що значно ускладнює розрахунки.

Рух джерела тепла поблизу краю тіла

У випадку зварювання поблизу краю пластини температура на вузькій стороні знаходиться застосуванням принципу накладення. Вузька пластина умовно добудовується до необмеженої і в добудованій частині симетрично до краю розміщується фіктивне джерело тепла такої ж потужності, як і реальне, яке рухається з такою ж швидкістю, що й реальне джерело тепла «паралельним курсом» (див. рис. нижче (а)).

Температура точок, розташованих поблизу краю вузької пластини знаходиться, як проста сума температур від двох однакових рухомих, або потужних швидкодіючих (в залежності від умов ведення процесу) джерел тепла: реального і фіктивного, розташованих симетрично відносно краю

241

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

пластини, при цьому кожне з них діє на точку зі свого радіуса вектора:

TA = Tреал + Tфікт ; Tреал = f (R); Tфікт = f (Rф )

Наприклад, у випадку застосування схеми розрахунків Рухоме лінійне джерело тепло в пластині з тепловіддачею (РЛД), буде:

Аналогічний прийом при необхідності використовується і для випадку руху джерела тепла поблизу краю масивного тіла, а також і для інших схем розрахунків.

Графічно цей процес зображено на рисунку вище (б), де подано розподіл температур (епюра) в поперечному напрямку поблизу краю тіла. Суцільні лінії означають реальні температури, пунктирні – фіктивні з умовою добудови тіла до необмеженого, TΣ – сумарна температура, обчислена згідно принципу накладення (суперпозиції), як сума приросту температури від реального і від фіктивного джерела тепла.

Нагрівання двох вузьких пластин рухомим джерелом

Для досить вузьких пластин, у яких обоє країв (І і ІІ) можуть впливати на температуру будь-якої точки, доводиться, після умовної добудови пластин до необмежених, вводити багаторазове відбиття тепла від країв, подаючи результуючу температуру теж як просту суму температур реального і всіх фіктивних джерел тепла.

Наприклад, для точки A з відомими координатами ( x, y ) обмежимось лише трьома складовими (див. рис. (а)): TА = T1 +T2 +T3 , з яких T1 це ре-

242

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

альна температура від дійсного джерела тепла в точці O на радіусі-векторі R , а інші – фіктивні температури від фіктивних джерел тепла в точках O′

Кожна з пластин (пунктир ліворуч і праворуч) умовно добудовується до необмеженої. В кожну добудовану частину поміщається фіктивне джерело тепла рівної потужності з реальним, яке рухається разом з ним з тією ж швидкістю. Відповідно, вклад кожного з джерел в суму температур в точці A визначається його радіус-вектором.

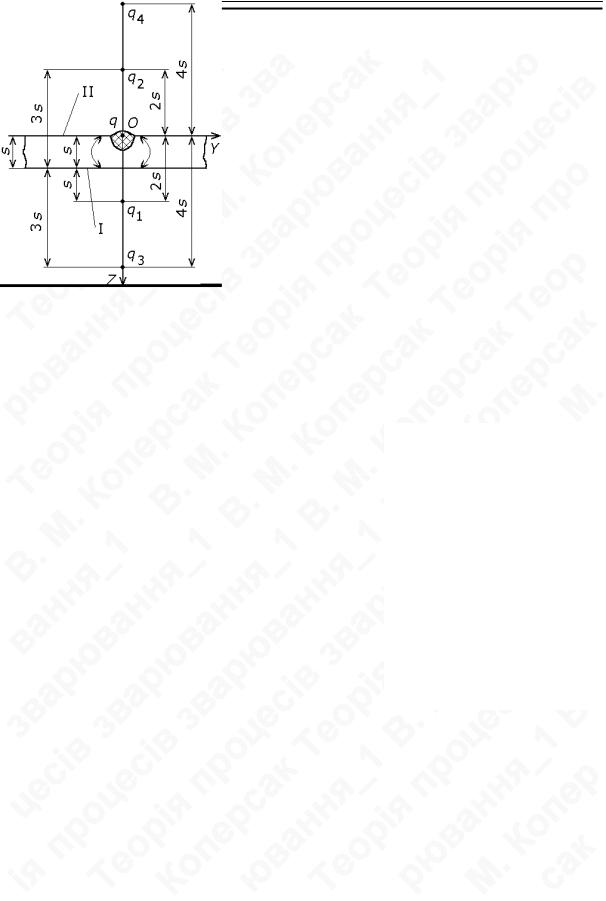
Нагрівання рухомим джерелом від краю тіла

В цьому випадку тіло теж добудовується до необмеженого, фіктивне джерело тепла поміщається в добудовану частину симетрично до обмежуючої поверхні (краю тіла), але фіктивне джерело тепла приймається рухомим, яке рухається від краю тіла в протилежному до руху реального джерела тепла напрямку з тією ж швидкістю.

Температура точок, розташованих поблизу краю тіла знаходиться, як і в попередніх випадках сумуванням температур реального та фіктивного джерел тепла (див. рис. (б)):

243

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Тут необхідно уважно слідкувати за тим, щоб в кожному випадку сумування врахувати зміщення фіктивного джерела тепла в протилежному від реального джерела тепла напрямку: x0 = f (t ,V ).

Рухоме точкове джерело тепла на поверхні пластини

Штучні прийоми, які застосовувались вище для спрощення крайових випадків розповсюдження тепла з успіхом можуть використовуватись і для більш складних ситуацій.

Наприклад, при малопотужному наплавленні на пластину (плоский шар), або зварюванні товстих пластин з неповним проваром (не на всю товщину за один прохід) доведеться враховувати багаторазове відбиття теплового потоку джерела тепла від зовнішніх поверхонь пластин (якщо пластини в повітрі, то поверхні можна вважати адіабатичними). Розглянемо це докладніше (див. рис.).

Нехай на поверхні пластини рухається точкове джерело тепла відомої потужності q .

Для спрощення оголосимо поверхні пластини адіабатичними. Потік тепла від q відбиваєть-

ся від площини I. Для того, щоб врахувати це явище, доводиться умовно добудовувати пластину до необмеженого тіла від поверхні І (так, як це робилось раніше, щоб застосувати

потім принцип накладення) і симетрично до поверхні І вводити фіктивне джерело q1 . Але потік тепла від q1 , в свою чергу, відбивається від повер-

хні II. Для того, щоб врахувати тепер ще й це явище, доводиться умовно добудовувати пластину до необмеженого тіла від поверхні ІІ і симетрично до поверхні ІІ вводити фіктивне джерело тепла q2 . Але тепло від q2 , в

свою ж чергу, теж відбивається від поверхні I. Тоді вводимо фіктивне дже-

244

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

рело q3 , а для нього відповідно вводимо q4 і так далі поки вистачить сил

(тобто, поки не досягнемо бажаної точності розрахунків). Всі ці умоглядні джерела тепла оголошуються однакової потужності q , рухаються симет-

рично і паралельно з однаковою швидкістю V , і їх радіуси-вектори до точки, в якій знаходиться температура, можуть бути легко обчислені через товщину пластини s , повторену кілька разів.

Температура будь-якої точки пластини визначається і в цьому випадку теж ґрунтуючись на принципі накладення (суперпозиції) як сума темпера-

При умові інтегрування у вказаних межах (0… ¥) це рівняння може бути зведене до розглянутої раніше схеми Рухомого лінійного джерела тепла в пластині РЛД (без врахування тепловіддачі, b = 0 ), з деякою поправ-

де: r − радіус вектор точки у площині пластин r = 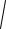x2 + y2 ,

ношення радіуса вектора r та товщини пластини s і в залежності від параметрів процесу зварювання знаходиться по номограмі, яка є наведена в довідковій літературі.

245

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Ізохрони, ізотерми та термічні цикли на поверхні пластини по конфігурації не відрізняються від уже розглянутих в схемі РЛД. Різниця є в розподілі температур по товщині пластини.

Температурне поле по товщині (по перерізу) пластини зображено тут на рисунку ізотермами для температур T1, T2 ... і т.д., причому:

T1 <T2 < T3 < T4 ....

По конфігурації ізотерм область термічного впливу в цьому

випадку можна поділити на три зони:

1)Поблизу джерела тепла (на відстані приблизно меншій товщини пластини) температурне поле наближається до поля точкового джерела на поверхні масивного тіла;

2)На великій відстані від джерела тепла (приблизно більше потроєної товщини) температурне поле подібне до поля в пластині від дії лінійного джерела тепла;

3)Перехідна зона – розташована між ними, її величина залежить від товщини пластини, потужності джерела тепла, властивостей матеріалу, ін.

Потужне швидкодіюче точкове джерело тепла на поверхні пластини

У випадку, коли виконується потужне наплавлення на пластину, або потужне зварювання пластин без повного провару, застосовують схему потужного швидкодіючого точкового джерела тепла на поверхні пластини.

Передумови в цьому випадку такі ж, як і для всіх потужних швидкодіючих джерел тепла: потужність джерела тепла q та швидкість зва-

246

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

рювання V умовно оголошуються необмежено великими, але границя їх відношення є деяка постійна величина, яка називається погонною енергією зварювання qП , що означає використання гіпотези одномоментного вико-

Розповсюдженням теплоти в повздовжньому напрямку в цьому випадку можна знехтувати, розглядаючи тільки розповсюдження теплоти вздовж осей OY i OZ . Таким чином, процес розповсюдження теплоти вважається таким, як від миттєвого точкового джерела тепла, яке виділило тепло в точці O в момент часу t = 0 .

Простота аналітичних рішень, притаманна схемам потужних швидкодіючих джерел тепла, дозволяє врахувати одночасно і тепловіддачу в зв’язку з охолодженням пластин в повітрі і відбиття теплових потоків від граничних поверхонь пластин.

При цьому процеси відбиття тепла від поверхонь (нижньої і верхньої) враховуються подібно до того, як це робилось в попередньому випадку. Приріст температури в точках пластин подається як добуток стандартного рівняння схеми розрахунків Потужного Швидкодіючого Лінійного Джерела тепла (ПШЛД) і деякої спеціальної функції F , яка враховує явище багаторазового відбиття теплових потоків від поверхонь пластини:

де: n = 0, 1; -1, 2; -2, 3; ... ; -¥, +¥;

247

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

В спеціальній літературі (В.В. Фролов) наведена номограма для розрахунку значень поправочної функції F (z,t )залежно від безрозмірних кри-

теріїв співвідношення координати z і товщини пластини s : zs та безроз-

мірного часу: t = ( a ×t )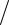s2 ;

Ізотерми на поверхні пластин, ізохрони та термічні цикли в цьому випадку мають вигляд, подібний до попередньої схеми розрахунків. Розподіл температур по товщині пластин якісно подібний до схеми Рухомого точкового джерела тепла на поверхні пластини, а кількісно визначається, звичайно, своїми залежностями, наведеними тут.

Слід зауважити, що для значень безрозмірного критерію τ > 0,5 , вели-

чина поправочної функції наближається до одиниці: F (z,t )≈1 і нею мож-

на знехтувати, застосувавши звичайну схему розрахунків ПШЛД. Використовуючи розглянуті в попередніх розділах принципи і спира-

ючись на прийняті нами спрощення і положення, можна знайти аналітичні вирази і для більш складних випадків (суцільний циліндр, несуцільний циліндр, оболонка, конус і т. ін.)

ВИБІР СХЕМИ РОЗРАХУНКІВ ТЕМПЕРАТУРНИХ ПОЛІВ ПРИ

ЗВАРЮВАННІ

Розглянуті вище типові та спеціальні схеми розрахунків температурних полів, а також методики їх застосування охоплюють основну масу практичних випадків більшості розповсюджених способів зварювання.

Для вирішення інженерних задач, виходячи з критеріїв величини швидкості зварювання, теплофізичних властивостей матеріалу, співвідношення глибини провару і товщини виробу, ін., цілком реально підібрати

248

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

одну з наведених методик.

При цьому можна керуватись методологічною класифікацією, що наведена тут на рисунку.

Шлях вибору схеми розрахунку:

Рухоме чи потужне швидкодіюче джерело тепла? Це залежить від співвідношення швидкості руху джерела зварювального нагрівання і швидкості розповсюдження теплоти в тілі (швидкості вирівнювання температур). Остання, в свою чергу, визначається переважно величиною коефіцієнта теплопровідності матеріалу тіла. Чим більше значення має коефіцієнт теплопровідності, тим при більшому значенні швидкості руху джерела тепла відбувається перехід від схем рухомих до схем потужних швидкодіючих джерел.

Ґрунтуючись на досвіді такого роду обчислень можна рекомендувати наступні (див. таблицю) критерії швидкості зварювання (чи наплавлення) для переходу від схем розрахунків рухомих джерел тепла (при менших значеннях швидкості руху) до схем розрахунків потужних швидкодіючих джерел тепла (при більших значеннях швидкості руху):

249

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Напівобмежене тіло, плоский шар чи пластина? Це залежить від величини виробу, його маси, а головне, від співвідношення глибини проплавлення і товщини виробу, який зварюється. В практиці зварювальних розрахунків для вибору конфігурації тіл прийнято вважати справедливими такі критерії співвідношення глибини провару ( hпр ) і товщини виробу ( s ):

hпр 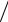s <110 − точкові джерела на поверхні масивних тіл; hпр s <110...2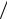3 − точкові джерела на поверхні пластин; hпр 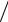s > 23 − лінійні джерела в пластинах.

Точкове джерело тепла чи лінійне? Тут вибір зовсім простий: схеми лінійних джерел тепла застосовуються тільки для пластин.

Слід зауважити, що жодна з розглянутих схем не може вказати точну температуру точки конкретного зварюваного виробу в точно визначений час. Кількість зроблених на шляху виводу аналітичних рівнянь припущень і їх якість – робить це неможливим. Розглянуті розрахункові схеми можуть претендувати лише на аналіз характеру розподілу температур в тілі, тобто давати відповідь на питання про відносну величину областей основного металу, які нагріваються до заданих температур при різних режимах зварювання, про характер розташування таких областей.

Для більш точних розрахунків доводиться вирішувати диференційне рівняння теплопровідності чисельними або іншими доступними методами, з застосуванням комп’ютерних технологій різного ступеню складності. При цьому, однак, теж не вдається врахувати всі реальні обставини і особливості процесу передачі тепла від джерела нагрівання до рідкого металу зварювальної ванни і далі в основний метал. Якщо спрощені схеми дають вірогідність відповідності розрахунків і практичних результатів порядку 20…50 %, то найскладніші обчислення на найпотужніших комп’ютерах можуть підвищити вірогідність співпадінь не точніше ніж до 10%.

250