Джерела нагрівання та

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

вість адитивності: вона вираховується, як сума вольт-амперних характеристик окремих областей дуги: стовпа дуги, катодної області та анодної об-

ласті: U д (Iд )= U ст (Iд )+U к (Iд )+U а (Iд )

Вольт-амперна характеристика стовпа дуги

Вивід вольт-амперної характеристики стовпа дуги передбачає ряд домовленостей (припущень), які історично склались серед інженерів та науковців, дослідників процесів дугового зварювання і які часто-густо навіть не озвучуються, вважаючись такими, які розуміються самі собою. Але ми спробуємо навести їх тут в усій можливій повноті:

1.Розглядаємо стійкий (усталений) дуговий процес. Енергія постачається в дугу в необмеженій кількості і як завгодно довго тривалий час, ніякі зовнішні фактори (в т.ч. й діаметр електродів) не впливають на діаметр дуги – вона може вільно необмежено розширюватись (або звужуватись) виключно за рахунок внутрішніх, притаманних їй процесів (вільна дуга).

2.В усіх областях дуги строго підтримується термодинамічна рівновага, при цьому гази стовпа дуги являють собою квазінейтральну плазму (підкоряється закону Сага).

3.Стовп дуги описується каналовою моделлю К.К. Хрєнова: тобто, стовп дуги приймають електронейтральним, циліндричним за формою, однорідним, з постійними по перетину температурою та густиною струму, довжина стовпа дуги приймається рівною довжині дуги (відстані між електродами), падіння напру-

ги в стовпі дуги пропорційне його довжині: Ucт = ЕстLд. 4. Перенос струму в стовпі дуги здійснюється тільки електрона-

ми, густина струму i описується рівнянням, виведеним раніше:

101

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

i =C x Eст

Qe T

де: x - ступінь іонізації газу в стовпі дуги;

Eст - напруженість електричного поля в стовпі дуги;

T - температура газу в стовпі дуги (абсолютна, [К]);

Qe - перетин Рамзауера взаємодії часток з електронами;

5.Стовп дуги являє собою циліндр, зовнішня поверхня якого чітко відділяє плазму дуги з температурою T від навколишнього

середовища, температура якого приймається рівною нулю:

Tc = 0 .

6.Всі теплові втрати стовпа дуги ( Rст) є втрати лише на випро-

мінювання електромагнітних хвиль (світлових та близьких до них - теплових інфрачервоних) із зовнішньої циліндричної оболонки дуги. Питання масообміну з навколишнім середовищем не розглядаються.

7.Розжарена плазма стовпа дуги оголошується абсолютно чорним тілом і її випромінювання підкоряється закону Стефана-

Домовившись про такі припущення, можна приступати до аналітичного виводу вольт-амперної характеристики стовпа дуги.

102

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Хід суджень при цьому такий:

При всіх постійних параметрах температура стовпа дуги залишається стабільною: вона не збільшується і не зменшується в процесі горіння дуги, якщо нічого не міняти. Це значить, що стовп дуги знаходиться в постійній енергетичній рівновазі з навколишнім середовищем, тобто: скільки тепла виділяється в стовпі дуги, стільки його й поглинається навколишніми тілами. Ця теза легко виражається математично рівнянням теплового балансу:

Rст = Qст

Відповідно до припущення № 6 вся енергія, яка втрачається стовпом дуги ( Rст), йде на випромінювання (закон Стефана - Больцмана).

Виділення енергії в стовпі дуги ( Qст ) може бути визначено, як і для будь-якого іншого електричного провідника (в якому струм переносять

(повний час горіння дуги tд можна скоротити).

Тепер згадаємо припущення № 3 і будемо вважати дугу циліндром з відомим радіусом: rст і назвемо його радіус стовпа дуги. Це дає змогу знайти площу бокової поверхні стовпа, яка випромінює теплоту ( Fст ), як площу циліндричної поверхні радіусом rст :

Fст = 2prст × Lд

Отже, рівняння теплового балансу стовпа дуги буде: s ×Т 4 × 2 prст × Lд = Ід ×U ст ;

ліву і праву частини останньої рівності можна поділити на довжину

103

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

дуги Lд, яка ні при яких обставинах (якщо дуга горить) не може бути рівна

В лівій частині одержаної рівності довжина дуги Lд скорочується, а в правій - утворюється відношення падіння напруги в стовпі дуги U ст до довжини дуги Lд (вірніше, стовпа дуги). А це є не о інше, як напруженість електричного поля стовпа дуги: U ст 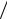Lд = Ест .

Відповідно до цих умов отримаємо вираз: sТ 4 × 2 prст = ІдEст , з яко-

го можна знайти:

З іншого боку, струм дуги, як і будь-якого провідника визначається добутком густини струму на площу перетину провідника:

Iд = iст × p rст2

Враховуючи припущення № 4 і щойно отриману залежність для раді-

Останню залежність вирішимо відносно напруженості електричного

Для вільної дуги характерна невисока ступінь іонізації ( x < 5...10 %), яка може бути виражена з рівняння Сага спрощеної форми (виводилося

Всі складові частини цього рівняння докладно описувались вище.

104

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Цей вираз підставимо у щойно отримане рівняння для напруженості

Тепер виконаємо необхідні алгебраїчні перетворення і добудемо кубічний корінь з лівої і правої частин:

перетворень одержимо рівняння вольт-амперної характеристики дуги:

Ліва і права частини цього рівняння можуть бути помножені на довжину дуги, як величину, яка ніколи не може бути рівна нулю, якщо дуга горить (існує) Lд ¹ 0 . Після такої маніпуляції отримаємо залежність, відо-

му в науково-інженерних колах як рівняння вольт-амперної характери-

стики вільної дуги Погодіна-Алєксєєва – Брауна:

105

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

спадаючу вольт-амперну характеристику стовпа дуги: при постійних умовах падіння напруги на дузі зворотно пропорційне 13 степені струму:

Uст ~ 31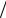Ід , що й спостерігається на практиці для дуг, діаметр яких не об-

межений в жодному перетині, тобто, вільних, або інакше таких, що вільно розширяються.

Принцип мінімуму Штейнбека

Термодинамічні принципи диктують, щоб енергетична ємність системи при самочинних процесах була мінімальною. Для усталеного, стійкого дугового процесу, це означає, що теплові втрати стовпа дуги повинні бути мінімально можливі для даних умов. Досліди показують, що залежність напруженості електричного поля вільної дуги від температури стовпа має яскраво виражений мінімум (див. рис.).

106

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Справді, як видно з рівняння вольтамперної характеристики вільної дуги По- годіна-Алєксєєва – Брауна для заданого складу газової фази і незмінних величинах струму в дузі Iд і тиску P електричне по-

ле дуги буде залежати тільки від температури стовпа дуги T .

Це явище формулюється, як принцип мінімуму Штейнбека:

Для усталеного, стійкого дугового процесу, при необмеженому жи-

вленні його електричною енергією, для дуги, яка не обмежена діамет-

ром в жодному своєму перетині (вільна, або така, що вільно розширя-

ється) фізичні процеси спрямовуються таким чином, щоб напруже-

ність електричного поля стовпа дуги була мінімально можливою для даних умов:

Це твердження може проілюструвати такий хід суджень:

1.При спонтанному збільшенні температури стовпа від TE збільшу-

ється ступінь іонізації, рухливість електронів, густина струму, напруженість електричного поля, одночасно збільшиться і перетин дуги, наслідком чого буде збільшення витрат енергії на випромінювання, яке приведе до зменшення температури в точку TE .

2.При спонтанному зменшенні температури стовпа від TE зменшу-

ється ступінь іонізації, густина струму, погіршується електрична провідність (збільшується опір) газів дугового проміжку, що збільшує напруженість електричного поля, одночасно зменшиться діаметр дуги, наслідком чого буде зменшення витрат енергії на випромінювання, яке приведе до збільшення температури в точку TE .

Аналогічним чином і спонтанні зміни напруженості електричного по-

107

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

ля, при інших постійних параметрах, компенсуються фізичними процесами в дузі таким чином, що для заданих умов зберігається мінімально можлива напруженість електричного поля та притаманна їй температура стовпа дуги.

Таким чином, при умові відсутності обмежень на діаметр і при необмеженому живленні електрикою, дуга в широких межах є саморегульована система. В дузі автоматично підтримується мінімально можлива напруженість електричного поля. Тобто, при постійних значеннях фізичних параметрів середовища, в якому горить дуга і струму в дузі ( Iд ), в стовпі дуги встановлюються такі значення температури (T ) і радіусу ( rст ), при яких напруженість поля в стовпі буде мінімальною.

Про температуру стовпа дуги

Знаючи рівняння вольт-амперної характеристики дуги і користуючись принципом Штейнбека температуру стовпа дуги, яка вільно розширяється, (T ) можна вирахувати аналітично, як мінімум (точка екстремуму) функції залежності напруженості електричного поля від температури: Eст = f (T ).

Такою функцією − яка пов’язує напруженість електричного поля і темпе-

ратуру стовпа − може послужити вольт-амперна характеристика дуги

(ВАХ). Як відомо з математичного аналізу − для того, щоб знайти екстремум функції потрібно виконати такі дії:

1.Взяти похідну функції.

2.Прирівняти її до нуля.

3.Знайти дійсні корені рівняння.

Для спрощення спочатку логарифмуємо рівняння вольт-амперної характеристики дуги, згруповуючи його члени так, як це вигідно для подальших перетворень:

108

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Отримане рівняння диференціюємо ( dEст dT ) згідно з таблицею по-

хідних, приймаючи постійними величини, по яких не буде проводитись

Рівність похідної нулю, d Ест = 0 , означає й рівність нулю правої ча-

Аце можливо в трьох випадках:

1.Ест = 0 – рівність нулю напруженості електричного поля озна-

чає, що відсутність самого поля, отже, дуга не горить (не існує), нічого не відбувається.

2.T → ∞ – це відповідає 100% іонізованій плазмі, чого в даному випадку не спостерігається.

3.29 = е0Ui - ймовірний і можливий випадок, заперечень не ви12 6kT

кликає. Очевидно, що саме він і відповідає звичайній електричній зварювальній дузі.

Остання умова (№3) дає змогу знайти температуру стовпа дуги, яка відповідає мінімуму напруженості електричного поля в стовпі. А вище було доведено, що цей мінімум підтримується у вільній дузі автоматично (дуга є саморегульована система). Отже, для вільної (такої, що вільно розширяється) дуги це й буде єдино можлива для даних умов:

109

В.М. Коперсак Теорія процесів зварювання-1. Джерела зварювального нагрівання та теплові процеси при зварюванні

Очевидно, що знайдена з останньої залежності температура дуги якраз і відповідає мінімальній напруженості електричного поля в дузі, яка підтримується дугою, як саморегульованою системою (згідно принципу мінімуму Штейнбека). Отже, буде підтримуватись постійною і температура дуги.

Звідси можна зробити важливий висновок:

Температура стовпа вільної дуги є величина постійна для даних умов і залежить тільки від потенціалу іонізації газу стовпа дуги Ui

(для суміші газів − від ефективного потенціалу іонізації Uеф ).

Якщо в наведену залежність підставити відомі вже значення постій-

них величин − заряду електрона e0 і постійної Больцмана k , то температу-

Це добре узгоджується з емпіричними залежностями, отриманими дослідним шляхом (вони іноді називаються формулами К.К.Хрєнова):

−для зварювання покритим електродом: T » 805 ×Ui

−для зварювання в середовищі захисних газів: T » 1000 ×Ui *;

−для механізованого зварювання під флюсом: T » 1100 ×Ui *;

*Примітка: при зварюванні в середовищі захисних газів і при механі-

зованому зварюванні під флюсом дуга не може вважатись зовсім вільною (такою, що вільно розширяється), але скоріше є перехідна до стисненої бо часто буває обмежена діаметром одного з електродів.

Спрощена форма запису вольт-амперної характеристики дуги

Використання принципу мінімуму Штейнбека, який постулює мінімально можливу для даних умов напруженість електричного поля в стовпі дуги, дозволяє спростити рівняння вольт-амперної характеристики стовпа,

110