
- •Введение
- •Общие рекомендации студенту по самостоятельной работе над математическими курсами
- •1.2. Арифметические векторы. Линейные операции над векторами. n-мерное арифметическое пространство
- •2. Системы векторов
- •2.1. Линейная зависимость векторов. Системы векторов.
- •2.3. Эквивалентные системы векторов
- •3.1. Матрицы. Основные определения
- •3.2. Операции над матрицами и их свойства
- •3.3. Определитель матрицы.
- •3.3.1. Определители второго порядка
- •3.3.2. Определители n-го порядка
- •3.3.3. Определители третьего порядка
- •3.3.4. Свойства определителей
- •3.4. Обратная матрица, ее свойства и вычисление
- •3.4.1. Решение матричных уравнений с помощью обратной матрицы
- •3.4.2. Нахождение обратной матрицы с помощью элементарных преобразований ее строк.
- •3.5. Ранг матрицы
- •3.5.1. Понятие минора k-го порядка матрицы. Определение ранга матрицы
- •3.5.2. Элементарные преобразования. Вычисление ранга матрицы с помощью элементарных преобразований
- •3.5.3. Понятие линейной зависимости строк (столбцов) матрицы. Другое определение ранга матрицы
- •4. Системы линейных алгебраических уравнений
- •4.1. Основные понятия
- •5. Геометрия пространства Rn
- •5.1. Прямые в R2
- •5.1.1. Уравнение линии на плоскости R2
- •5.1.2. Общее уравнение прямой
- •5.1.3. Уравнение прямой с угловым коэффициентом
- •5.1.4. Уравнение прямой, проходящей через данную точку
- •в заданном направлении. Уравнение пучка прямых
- •5.1.6. Уравнение прямой в отрезках
- •5.1.7. Нормальное уравнение прямой
- •5.1.8. Расстояние от точки до прямой
- •5.1.9. Угол между прямыми. Условия параллельности
- •и перпендикулярности двух прямых
- •5.1.10. Точка пересечения двух прямых
- •5.2. Прямая и плоскость в пространстве
- •5.2.1. Канонические уравнения прямой
- •5.2.3. Векторное и параметрические уравнения прямой
- •5.2.4. Угол между прямыми. Взаимное расположение двух прямых
- •5.2.5. Общее уравнение плоскости
- •5.2.6. Уравнение плоскости в отрезках
- •5.2.8. Нормальное уравнение плоскости
- •5.2.9. Расстояние от точки до плоскости
- •5.2.10. Взаимное расположение двух плоскостей
- •5.2.11. Общие уравнения прямой
- •5.2.12. Взаимное расположение прямой и плоскости
- •5.3. Гиперплоскость в пространстве Rn
- •5.4. Выпуклые множества
- •6. Теория пределов последовательностей
- •6.1. Числовые последовательности
- •6.1.3. Свойства бесконечно малых последовательностей.
- •6.2. Сходящиеся последовательности
- •6.2.1. Определение предела последовательности.
- •6.2.2. Свойства сходящихся последовательностей.
- •7. Предел и непрерывность функции
- •7.1. Понятие функции одной переменной.
- •7.1.1. Определение функции. Элементарные функции.
- •7.1.2. Свойства функции одной независимой переменной.
- •7.1.3. Некоторые функциональные зависимости, используемые в экономике.
- •7.2. Предел функции
- •7.2.1. Понятие предела функции в точке.
- •7.2.2. Теоремы о пределах функций.
- •7.2.3. Замечательные пределы.
- •7.2.4. Бесконечно малые и бесконечно большие функции.
- •7.2.5. Сравнение бесконечно малых функций.
- •7.2.6. Раскрытие неопределенностей.
- •7.3. Непрерывность функции
- •7.3.1. Непрерывность функции в точке и на множестве.
- •7.3.2. Арифметические действия над непрерывными функциями.
- •7.3.3. Непрерывность сложной и обратной функции.
- •7.3.4. Точки разрыва функции и их классификация.
- •7.3.5. Свойства функций, непрерывных на отрезке.
- •8.1. Производная
- •8.1.2. Геометрический смысл производной. Уравнения касательной и нормали к плоской кривой. Угол между кривыми.
- •8.1.3. Физический смысл производной.
- •8.1.4. Непрерывность дифференцируемой функции.
- •8.1.5. Основные правила дифференцирования.
- •8.1.6. Таблица производных основных элементарных функций.
- •8.1.7. Производная степенно-показательной функции.
- •8.1.8. Примеры вычисления производных.
- •8.1.9. Производная неявной функции.
- •8.2. Дифференциал
- •8.2.1. Понятие дифференциала функции в точке. Геометрический смысл дифференциала.
- •8.2.2. Применение дифференциала к приближенным вычислениям.
- •8.2.3. Производные и дифференциалы высших порядков.
- •8.2.4. Основные теоремы о дифференцируемых функциях.
- •8.2.5. Правило Лопиталя раскрытия неопределенностей.
- •8.3. Исследование функций с помощью производных
- •8.3.1. Условия постоянства, возрастания и убывания функций.
- •8.3.3. Наибольшее и наименьшее значения функции на отрезке.
- •8.3.4. Выпуклость и вогнутость графика функции.
- •8.3.5. Асимптоты графика функции.
- •1. Многомерное арифметическое пространство
- •Тренировочное задание 1
- •Решение тренировочного задания 1
- •2. Системы векторов
- •Тренировочное задание 2
- •Решение тренировочного задания 2
- •3. Матрицы и определители
- •3.1. Матрицы и операции над ними
- •Тренировочное задание 3.1
- •Решение тренировочного задания 3.1
- •3.2. Определители и их свойства
- •Тренировочное задание 3.2
- •Решение тренировочного задания 3.2
- •4. Системы линейных уравнений
- •Тренировочное задание 4
- •Решение тренировочного задания 4
- •5. Аналитическая геометрия
- •5.1. Элементы аналитической геометрии на плоскости
- •Решение тренировочного задания 5.1
- •5.2. Элементы аналитической геометрии в пространстве
- •Тренировочное задание 5.2
- •Решение тренировочного задания 5.2
- •6. Сходимость числовых последовательностей.
- •Тренировочное задание № 6.
- •Решение тренировочного задания № 6.
- •7. Предел и непрерывность функции.
- •Тренировочное задание № 7.
- •Решение тренировочного задания № 7.
- •8. Дифференциальное исчисление функций одной переменной.
- •Тренировочное задание № 8
- •Решение тренировочного задания № 8.
8.1.3. Физический смысл производной.
С физической точки зрения разностное отношение ∆f (x0 ) явля-
∆x
ется средней |
скоростью |
изменения функции |
f (x) |
на отрезке |
|
[x0 |
, x0 +∆x], а |
тогда lim |
∆f (x0 ) = f ′(x0 ) называется |
мгновенной |
|
|
|
∆x→0 |
∆x |
|
|
скоростью изменения функции f (x) в точке x0 . |
|
|
|||
|
Так, например, если функция S = f (t) задает зависимость пути |
||||
S , |
пройденного некоторым телом, от времени |
t , то производная |
|||
f ′(t) = v(t) является скоростью движения; если функция V = f (t) вы-
ражает зависимость количества производимой продукции от времени t , то ее производная V ′ = f ′(t) = p(t) является производительностью
труда в момент времени t .
8.1.4. Непрерывность дифференцируемой функции.
Теорема 8.1. Если функция y = f (x) имеет производную в точке x0 , то она непрерывна в этой точке.
Обратное утверждение верно не всегда. Существуют непрерывные в точке x0 функции, не имеющие в этой точке производной
(пример 8.3). |
|
|
|
8.1.5. Основные правила дифференцирования. |
|
||
Пусть |
D1 ― множество точек из области определения функции |
||
y = f (x) , в каждой из которых существует производная |
′ |
||
f (x) . Тогда |
|||
каждому |
значению x D1 соответствует |
′ |
задана новая |
f (x) , т.е. |
|||
|
′ |
D1 . Процесс нахождения |
|
функция y = f (x) с областью определения |
|||
производной называется дифференцированием и осуществляется по некоторым формальным правилам. Напомним эти правила.
Теорема 8.2. Производная постоянной равна нулю: т.е. если y = C , то y′ = C′ = 0 .
Теорема 8.3. Если функции u = f (x) и v = g(x) имеют производ-
ные в точке x , то в этой точке имеют производные сумма, разность, произведение и частное этих функций (частное при условии, что g(x) ≠ 0 ), причем :
106

1)(u ±v)′ = u′±v′ производная суммы (разности) равна сумме (разности) производных;
2)(uv)′ = u′v +uv′ производная произведения равна произве-
дению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго сомножителя;
|
u |
' |
′ |
′ |
|
|
|
|
3) |
= |
u v −uv |
|
|
|
производная частного равна дроби, знаме- |
||
|
|
|
|
|
|
|||
v2 |
|
|
|
|||||
|
v |
|
|
|
|
|
||
нателем которого является квадрат знаменателя, а числителем служит разность между произведением производной числителя на знаменатель и произведением числителя на производную знаменателя.
|
|
|
′ |
′ |
− |
постоянный множитель выносится за |
|||||||
Следствие: (cu) = c u |
|
||||||||||||
знак производной; |
|
|
|
|
|
|
|
|
|
|
|
||
|
′ |
′ |
|
′ |
|
|
|
|
′ |
|
|
|
|
4) (uv...w) |
= u v...w +uv ...w + +uv...w |
|
|
|
|
||||||||
Теорема 8.4. (производная сложной функции ). Если функция |
|||||||||||||
y = g(x) |
имеет производную в точке x0 , а функция |
z = f (y) имеет |
|||||||||||
производную |
в |
точке |
|
y0 = g(x0 ) , |
то |
сложная |
функция |
||||||
z = F(x) = f (g(x)) |
имеет |
|
производную |
в |
точке |
x0 и |
|||||||
F′(x0 ) = f ′(y0 )g′(x0 ). |
|
|
|
|
|
|
|
|
|
|
|||
Теорема 8.5. (производная обратной функции). Пусть функция |
|||||||||||||
y = f (x) |
в некоторой окрестности точки |
x0 |
является строго моно- |
||||||||||
тонной, |
непрерывной и |
существует производная |
f ′(x0 ) , |
причем |
|||||||||
f ′(x0 ) ≠ 0 . Тогда |
существует |
обратная |
функция |
x = f −1(y) = g(y) , |
|||||||||
определенная в некоторой окрестности точки |
y0 = f (x0 ) , строго м о- |
||||||||||||
нотонная, непрерывная и обратная функция имеет производную |
|||||||||||||
|
|
|
g′(y0 ) = |
1 |
|
|
|
|
|
(8.8) |
|||
|
|
|
f ′(x0 ) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
107

8.1.6. Таблица производных основных элементарных функций.
Запишем таблицу производных основных элементарных функций, учитывая правило дифференцирования сложной функции:
1. |
y = c = const, |
y′ = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2. |
y = x, |
|
|
y′ =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
3. |
y = u, |
|
|
y |
′ |
= u . |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
y = uα |
(α = const), |
y′ =α uα−1 u′ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. |
y = u , |
y′ |
= |
|
u |
|
|
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
u |
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
y |
′ |
|
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|
|
|||||||
|
y = u , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6. |
|
= −u2 . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
7. |
y = a |
u |
|
(a > 0, a ≠1), |
y |
′ |
= a |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|||||||
|
|
|
|
|
|
|
ln a u . |
||||||||||||||||||||||
8. |
y = e |
u |
, |
|
y |
′ |
= e |
u |
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
u . |
|
|
|
|
|
|
|||||||||||||||
9. |
y = loga u, |
y′ = |
|
|
|
|
|
u′ |
|
|
|
. |
|
|
|
|
|
||||||||||||
|
u ln a |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
y = ln u, |
y′ |
|
|
u′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10. |
= |
|
u . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
11. |
y = sin u, |
y′ = cosu u′ |
|||||||||||||||||||||||||||
12. |
y = cosu, |
y |
′ |
= −sin u |
|
|
|
′ |
|||||||||||||||||||||
|
u . |
||||||||||||||||||||||||||||
13. |
y = tgu, |
y′ |
= |
|
|
|
|
|
u′ |
|
|
. |
|
|
|
|
|
||||||||||||
|
cos2 u |
|
|
|
|
|
|||||||||||||||||||||||
|
y = ctgu, |
y |
′ |
|
|
|
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|
|
||||||||
14. |
= −sin2 u . |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
y = arcsin u, |
y |
′ |
= |
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
15. |
|
|
1−u2 . |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
16. |
y = arccosu, |
y′ |
= − |
|
|
|
u |
′ |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
1−u2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
17. |
y = arctgu, |
y′ |
= |
|
|
|
|
|
u′ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
1+u2. |
|
|
|
|
|
|
|
|||||||||||||||||||||
18. |
y = arcctgu, |
y′ |
= − |
|
|
|
u′ |
|
|
|
|
|
|
|
|
|
|||||||||||||
1+u2. |
|
||||||||||||||||||||||||||||
108

8.1.7. Производная степенно-показательной функции.
Пусть функции u(x) |
и v(x) имеют производные в некоторой |
|
точке x X , причем на |
X |
определена функция y = (u(x))v(x) , где |
u(x) > 0. Тогда функция y |
имеет производную в точке x , причем ее |
|
можно найти с помощью логарифмического дифференцирования
(8.9): так как y = f (x) = (u(x))v(x) |
(u(x) > 0), |
|
|
||||||||||||||||||
то ln |
|
y |
|
= ln |
|
|
(u(x))v(x) |
|
|
|
= v(x) ln(u(x)) . |
|
|
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
Тогда |
|
|
(ln |
|
y |
|
)′ = v′(x)ln(u(x)) + v(x)u′(x) . |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)′= |
y′ |
|
u(x) |
|
|
Учитывая, что (ln |
|
y |
|
|
|
|
|||||||||||||||
|
|
, |
получаем окончательно |
|
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
|
y |
|
||||||||||||||||||
|
|
′ |
|
|
|||||||||||||||||
|
|
y′ = (u(x))v(x) |
|
|
|
|
|
(8.10) |
|||||||||||||
|
|
|
v′(x)ln(u(x)) + v(x)u (x) |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(x) |
|
|
||||
Формулу (8.10) не следует заучивать, надо запомнить прием, использованный при выводе этой формулы.
8.1.8. Примеры вычисления производных.
Приведем несколько типичных примеров вычисления производных. Пример 8.5. Найти производные следующих функций:
1) y = arcsin a2 − x2 ; a2 + x2
4) y = ln 
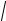 x2 +1 − x ;
x2 +1 − x ; 
 x2 +1 + x
x2 +1 + x
2) y = arctg |
1− x |
; 3) |
y = ln(emx +e−mx ) ; |
|
1+ x |
|
|
|
5 |
|
|
5) y = |
(x −1)2 |
; |
6) y = x |
1 |
. |
|
3 |
7 |
x |
||||
|
(x −2)4 |
(x −4)3 |
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
′ |
|
|
|
a2 − x2 ′ |
|
|
|
−2x(a2 + x2 ) −2x(a2 − x2 ) |
|
||||||||||||
|
|
a2 |
− x2 |
|
|
|
|
2 |
+ x |
2 |
|
|
|
|
|
|
(a2 + x2 )2 |
|
|
|
||||||||
1) |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
arcsin |
a |
2 |
+ x |
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a2 − x2 2 |
|
(a2 |
+ x2 )2 −(a2 |
− x2 )2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
+ x |
2 |
|
|
|
|
(a2 + x2 )2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= |
|
|
−4a2 x |
|
|
|
= − |
|
|
|
2a |
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
a2 |
+ x2 |
|
|
|
|
|
|
|
|
|||||||||
|
(a2 + x2 ) 4a2 x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
109

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− x ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
1 |
+ x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
− x ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
arctg |
1 |
= |
|
|
|
1 |
+ x |
|
|
|
= |
|
1+ x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1− x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
+ x |
1 |
+ |
|
|
|
1− x |
|
|
|
1+ |
|
|
||||||||||
|
|
|
|
|
|
1+ x |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1+ x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= − |
|
1 |
|
|
|
|
= − |
|
|
|
|
1 |
|
|
|
; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
2(1+ x) |
|
1− x |
1− x2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
−(1+ x) −(1− x) |
|||
|
|
|
(1+ x)2 |
||
= |
|
|
|
|
= |
2 |
|
|
1+ x +1− x |
||
|
1− x |
||||
|
|
|
1+ x |
1+ x |
|
|
|
|
|
|
|
(e |
mx |
+e |
−mx |
) |
′ |
|
(e |
mx |
′ |
−mx |
) |
′ |
|
|
3) (ln(e |
mx |
+e |
−mx |
′ |
|
|
|
= |
|
) +(e |
|
|
= |
|||||||
|
|
)) = |
emx +e−mx |
|
|
|
emx +e−mx |
|
|
|||||||||||
= |
emx (mx)′+e−mx (−mx)′) |
= emxm +e−mx (−m) |
= m(emx −e−mx ) . |
|||||||||||||||||
|
||||||||||||||||||||
|
|
|
emx +e−mx |
|
|
|
|
|
emx +e−mx |
|
|
emx +e−mx |
||||||||
4) Здесь, предварительно упростим выражение для y , а затем будем его дифференцировать. Имеем:
|
|
|
|
|
|
( |
x2 |
+1 |
− x)2 |
|
( |
x2 |
+1 |
− x)2 |
|
||||
y = ln |
|
x2 |
+1 − x |
= ln |
= ln |
= |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 +1 |
− x2 |
|||||||
|
x2 +1 + x |
( x2 +1 + x)( x2 +1 − x) |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||
= 2ln(
 x2 +1 − x) .
x2 +1 − x) .
Теперь дифференцируем: y′ = (2ln( |
|
|
|
− x))′= 2( |
|
x2 +1 |
− x)′ = |
|||||||||||||||||||||||
x2 +1 |
||||||||||||||||||||||||||||||
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
+1 − x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2x |
|
|
x − |
x |
2 |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
−1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
x2 +1 |
|
|
|
|
|
x2 |
+1 |
|
|
|
|
2 |
|
|
|
|
|
|
||||||||
= |
|
|
|
= |
|
|
|
|
= − |
|
|
. |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x2 +1 − x |
|
|
|
x2 +1 − x |
|
x |
2 +1 |
|
|
|
|
|
|
||||||||||||||
5) Вначале найдем логарифм от функции y : |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ln y = |
5 ln(x −1) − 3 ln(x −2) − 7 ln(x −4). |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
3 |
|
|
|
|
|
|||||||
Дифференцируя это равенство, находим:
yy′ = 52 x1−1 − 34 x −1 2 − 73 x −1 4 .
110

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
y′ = y |
|
|
|
|
|
|
− |
|
|
|
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
2(x −1) |
|
4(x −2) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3(x −4) |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
= |
|
|
|
(x |
−1) |
2 |
|
|
|
|
|
|
5 |
|
|
− |
|
|
|
3 |
|
− |
|
|
|
7 |
|
= |
|
(x −1) |
2 |
= |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
7 |
|
|
|
|
|
|
|
4(x −2) |
3(x −4) |
|
3 |
7 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2(x −1) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
(x −2)4 (x −4)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x −2)4 (x −4)3 |
|
||||||||||||||
= |
30(x2 −6x +8) −9(x2 −5x +4) −28(x2 −3x +2) |
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
12(x −1)(x −2)(x −4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
(7x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
= − |
+51x −148)(x −1)2 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
12(x −2)4 (x −4) 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
6. y = x |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вначале найдем логарифм от функции y : |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
ln y = |
1 |
|
|
|
1 |
= − |
1 |
ln x = − |
ln x |
. Дифференцируя это равенство, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
ln |
|
|
x |
x |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y |
′ |
|
|
|
|
|
|
|
′ |
−ln x |
(x) |
′ |
|
|
|
|
|
|
|
|
|
|
|
1 |
x −ln x |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
(ln x) x |
|
|
|
|
|
|
|
|
′ |
|
|
|
|
x |
|
|
|
|
|
|
||||||||||||||||
получим: |
y |
= − |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
или |
|
|
y |
= −y |
|
|
x2 |
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Отсюда: |
y′ |
|
|
|
1 |
ln x −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= |
x |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Наибольшие затруднения встречаются при дифференцировании сложной функции, поэтому следует запомнить, что дифференцирование производится в порядке, обратном тому, который существует при вычислении частного значения функции y для определенного
значения аргумента x .
Пример 8.6. Найти производную функции y = sin2 5x. Решение. Для вычисления y аргумент x : 1) умножается на 5;
2) отыскивается синус; 3) результат возводится во вторую степень. Следовательно, дифференцирование производится в обратном порядке, т.е. сначала дифференцируем степень, затем синус и, наконец, произведение на постоянную :
y = 2(sin 5x)(sin 5x)′ = 2sin 5x cos5x (5x)′ = 2sin 5x cos5x 5 = 5sin10x .
111
