5. Геометрия пространства Rn

5.1. Прямые в R2

5.1.1. Уравнение линии на плоскости R2

Уравнением линии на плоскости Оху называется равенство, содержащее переменные х и у, вида F(х, у)= 0, которому удовлетворя-

ют все точки данной линии и только они. Для вывода уравнения линии часто используются формулы:

а) расстояние между двумя точками М1(х1, у1 ) и М 2 (х2 , у2 ).

М1М = λ , то координаты точки М определяются по формулам:

ММ2

В частности, если точки М – середина отрезка М1М 2 , то λ = 1 и формулы (5.2) принимают вид:

тогда, согласно условию, имеем АМ = ВМ или по (5.1)

(х −1)2 +(у −3)2 = (х −3)2 +(у −1)2 .

Возведя обе части равенства в квадрат и упрощая, получим

х2 – 2х +1+ у2 – 6у +9 = х2 – 6х +9 + у2 – 2у +1,

откуда получаем у = х . Это серединный перпендикуляр, восставленный из середины отрезка АВ.

61

5.1.2. Общее уравнение прямой

Прямая L на плоскости определяется однозначно, если известны точка Мо = (хо , уо ), через которую она проходит и ненулевой вектор

n = (A, B), перпендикулярный прямой L. Пусть М (х, у) – произволь-

ная точка прямой L, r = (x, y) и r0 = (x0 , y0 ) – радиус-векторы точек М и М0 соответственно. Под радиус-вектором точки М понимается век-

тор ОМ с началом в точке О и концом в точке М. Уравнение

где С = – Ах0 – Ву0 , А2 + В2 ≠ 0. Справедлива теорема: всякое уравне-

ние первой степени относительно х и у (т. е уравнение вида (5.5)) определяет на плоскости некоторую прямую и наоборот, всякая прямая на плоскости определяется уравнением первой степени. Заметим, что век-

тор n = (A, B) определяется с точностью до постоянного множителя.

Ву +С = 0 (или у = b , где b = −CВ ), параллельна оси Ох.

(или у = 0, поскольку В ≠ 0 ), совпадает с осью Ох.

Поскольку уравнение (5.5) охватывает все возможные положения прямой на плоскости, оно называется общим уравнением прямой.

62

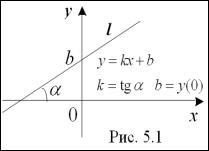
5.1.3. Уравнение прямой с угловым коэффициентом

Углом наклона прямой L к оси Ох

называется угол α , отсчитываемый от положительного направления оси до прямой L против движения часовой стрелки (рис. 5.1.). Если прямая параллельна оси Ох, то полагают α = 0 . Таким образом, угол наклона α удовлетворяет неравенству 0 ≤α <π .

Угловым коэффициентом прямой называется число, равное тангенсу угла наклона прямой к оси Ох: k = tgα . Из определения следует:

1)величина k может принимать любые действительные значения,

т.е. k R ;

2)прямая, параллельная оси ординат, не имеет углового коэффи-

циента, поскольку в этом случае α =π2 ; 3) всякая прямая, не параллельна оси Оу, имеет единственный уг-

Прямая L на плоскости определится однозначно, если известны точка В = (0, b), принадлежащая этой прямой и угловой коэффициент k этой прямой (Рис. 5.1). В этом случае уравнение прямой L имеет вид

которое называется уравнением прямой с угловым коэффициентом.

Число b, называемое начальной ординатой, показывает величину направленного отрезка, отсекаемого прямой L на оси ординат. При В ≠ 0 общее уравнение прямой (5.5) легко преобразуется в уравнение прямой с угловым коэффициентом (5.7):

k = − A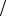B , b = −CB .

Частные случаи:

63

1. b = 0, k ≠ 0. Прямая, определяемая уравнением у = kх, прохо-

дит через начало координат;

2. k = 0, b ≠ 0. Прямая, определяемая уравнением y = b, парал-

лельна оси Ох;

3. k = 0, b = 0. Прямая, определяемая уравнением у = 0, совпадает с осью Ох.

5.1.4. Уравнение прямой, проходящей через данную точку

в заданном направлении. Уравнение пучка прямых

Если точка М0 = (х0 , у0 ) принадлежит прямой L и известен угловой коэффициент k этой прямой, то ее уравнение имеет вид

и называется уравнением прямой, проходящей через данную точку в за-

данном направлении. Если k "пробегает" все действительные значения k R , то уравнение (5.8) описывает множество прямых, проходящих че-

рез точку М0 и называется уравнением пучка прямых с центром в М0 .

5.1.5. Уравнение прямой, проходящей через две заданные

точки

Пусть прямая L проходит через точки М1 = (х1, у1 ) и М 2 = (х2 , у2 ), х1 ≠ х2 , у1 ≠ у2. Тогда ее уравнение имеет вид:

уравнением (5.9), то выполняется условие принадлежности трех точек одной прямой:

Вектор M1M2 (х2 − х1, у2 − у1 ) – направляющий вектор прямой L. Уравненияпрямой по направляющемуветру a(l, m) и точке (х0 , у0 ):

64