
- •Векторы и операции над ними
- •Понятие n-мерного векторного пространства
- •Скалярное произведение векторов
- •Угол между n-мерными векторами
- •Линейная зависимость векторов
- •Базис и ранг системы векторов
- •Ортонормированный базис
- •Матрицы. Основные понятия
- •Операции над матрицами
- •Определитель матрицы
- •Обратная матрица
- •Ранг матрицы
- •Линейное уравнение. Основные понятия
- •Системы линейных уравнений
- •Теорема Кронекера-Капелли
- •Метод обратной матрицы. Метод Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы уравнений
- •Собственные векторы и собственные числа
- •Использование алгебры матриц
- •Использование систем линейных уравнений
- •Системы координат на плоскости
- •Связь полярной и прямоугольной систем координат
- •Простейшие приложения метода координат на плоскости
- •Линии на плоскости. Основные понятия
- •Общее уравнение прямой
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой L, проходящей через две заданные точки
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Общее уравнение плоскости
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •Точки пересечения прямой и плоскости
- •Понятие числовой последовательности. Арифметические операции над последовательностями
- •Связь бесконечно больших и бесконечно малых последовательностей
- •Простейшие свойства бесконечно малых последовательностей
- •Свойства сходящихся последовательностей
- •Монотонные последовательности
- •Предел функции
- •Односторонние пределы
- •Свойства пределов функций
- •Сравнение функций
- •Непрерывность функции в точке
- •Свойства непрерывных функций
- •Односторонняя непрерывность. Точки разрыва и их классификация
- •Свойства непрерывных на отрезке функций
- •Определение производной и ее простейшие свойства
- •Геометрический смысл производной
- •О связи дифференцируемости и непрерывности функций
- •Логарифмическая производная
- •Таблица производных простейших элементарных функций
- •Производные высших порядков
- •Геометрический смысл дифференциала
- •Применение производной в экономике
- •Теорема Ферма (о равенстве нулю производной)
- •Сравнение функций по скорости роста
- •Формулы Маклорена и Тейлора
- •Разложение в ряд Маклорена элементарных функций
- •Условия возрастания и убывания функции
- •Понятие экстремума
- •Необходимое условие экстремума
- •Выпуклость функции. Точки перегиба
- •Схема исследования функции на выпуклость
- •Асимптоты графика функции
- •Исследование функций и построение их графиков
- •Эластичность функции
- •Свойства эластичности функции
- •Эластичность элементарных функций
- •Определение комплексных чисел
- •Традиционная форма записи комплексных чисел
- •Геометрическое изображение комплексных чисел
- •Операции над комплексными числами
- •Экспонента с комплексной переменной

Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 139 |
|
|
|
|
|
раическую структуру называют полем (поле действительных чисел, поле комплексных чисел). Отметим, что в зависимости от наличия (чаще всего отсутствия) тех или иных свойств в алгебраической структуре различают такие алгебраические объекты как группа, кольцо, тело.
3. Традиционная форма записи комплексных чисел.
Где же среди введенных новых чисел спрятано «хитроумное» мнимое
число i = |
−1 |
?! |
|
|
|
|
|
|
|
|
|
|
|
|
|
Из аксиомы 30 следует, что |
0 |
|
0 |
|
|
0 0 −1 1 |
|
−1 |
40 |
||||||
|
|
|
|
= |
0 |
1 |
+1 0 |
|
= |
0 |
|
=−1. |
|||
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||||
Тогда, если буквой |
« i » обозначить пару |
0 |
|
, то имеем |
i i = i2 = −1, т.е. |
|
|
||||
|
|
1 |
|
|
|
«мнимая единица» |
получила реальное истолкование как одной из пар, а |
||||
именно пары вида i = 10 .
Тогда любое комплексное число можно записать следующим образом
a |
a |
0 |
|
=1 |
a |
b |
|
0 |
|
=1 a +bi = a +bi |
(*) |
|||||
|
= |
0 |
|
+ |
|
|
0 |
|
+ |
0 |
|
|
|
|||
b |
|
|
b |
|
|
|
|
|
|
1 |
|
|
|
|||
Итак, комплексным числом называются числа вида z = a +bi где i2 = −1. Это традиционная алгебраическая форма комплексных чисел, При этом первая компонента называется действительной частью комплексного числа a = Re z , вторая – мнимая часть b = I m z .
Подчеркнем, что как Re z так и I m z есть действительные числа.! Следует
различать выражение, «мнимая часть комплексного числа» и «мнимое число». Множитель « i » в записи комплексного числа можно трактовать как
указание на то, что « b » есть вторая компонента пары |
a |
. При этом, чис- |
|
||
|
b |
|
ло z = a −bi является сопряженным для числа z = a +bi .
4. Геометрическое изображение комплексных чисел
Мы привыкли, что множество R удобно изображать точками на прямой. Как быть с новыми числами ?
Для геометрического истолкования комплексных чисел формулу (*) перепишем в виде

Лекция № 15 |
|
|
|
|
Комплексные числа |
|
|
|
|
|
проф. Дымков М. П. |
140 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a |
a |
0 |
|
a |
b |
|
0 |
|
1 |
a |
b |
0 |
|
1 |
|
0 |
|
||||||
z = a +ib = |
= |
|
+ |
|
=1 |
|
+ |
|
|
|
= |
0 |
|
0 |
|
+ |
|
|
= a |
|
+b |
|
|
b |
0 |
|
b |
|
|
0 |
0 |
|
1 |
|
|
|
|
0 |
1 |
|
0 |
|
1 |
|
|||
|
|
|
|
|
a |
можно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т.е. комплексное число z = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
трактовать как точку координатной плоскости или вектор OР с координатами а и b в единичном базисе
g1 |
1 |
|
, |
g2 |
|
0 |
|
|
= |
0 |
|
= |
|
. |
|||
|
|
|
|
|
1 |
|
||
b |
|
|
|
|
z = a + bi |
||
|
|
|
|
||||
|
|
i |
r |
Р(а;b) |
|||
|
|
|
|
|
|
||
g2 (0;1) |
|
|
|
ϕ 1 |
|
|
|
|
|
0 |
|
g1 |
(1;0) |
а |
|
|
|
|
|||||
|
|
|
|
|
|
||
Плоскость, на которой изображают комплексные числа называют плоскостью комплексной переменной. Ее ось абсцисс называют вещественной осью, а ось ординат – мнимой осью в соответствии с наименованием частей комплексного числа z.
Векторы g1 и g2 обычно не пишут (оставляют « 1 » на вещественной оси и « i » – мнимая единица на мнимой оси).
Легко видеть, что при этом сопряженное число z = a −bi – симметрично относительно действительной оси числу z = a +bi .
Кроме традиционной (алгебраической) записи комплексного числа существуют и другие их записи.
Рассмотрим комплексное число z = a +bi и изобразим его на плоскости в прямоугольной системе координат. Обозначим через r расстояние от 0 до точки Р(а; b), а через φ – угол , образованный лучом 0Р с положительным направлением действительной оси 0х, отсчитываем против часовой стрелки
(0 ≤φ < 2π ).
Число r называют модулем комплексного числа и обозначают r =| z | , число φ – аргументом (главным) и обозначают φ = arg z .
Очевидно, что |
|
|
||
r = |
|
, a = r cosφ b = r sinφ cosφ = a |
, sinφ = b . |
|
a2 +b2 |
||||
|
|
r |
|
r |
Тогда z = a +bi = r cosφ + r sinφ i = r(cosφ +isinφ) |
– тригонометриче- |
|||
ская форма записи комплексного числа.

Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 141 |
|||
Например: |
|
|
|
|
|
1) z = i | z |=1, |
φ = |
π |
(i =1 (cosφ +isinφ) = i), |
||
|
|
2 |
|
|
|
2)z =1 =1 (cos0 +isin 0) ,
3)−1 =1 (cosπ +isinπ),
|
|
|
|
π |
|
π |
|
|
4) |
1+i = 2 |
+isin |
||||||
cos |
4 |
4 |
. |
|||||
|
|
|
|
|
|
|||
5. Операции над комплексными числами
Речь идет об обычных операциях (сложение, вычитание, умножение, деление, выведение в степень, извлечение корней).
Удобство выполнения операций зависит от избранной формы представления комплексных чисел. Сразу же заметим, что представление ком-
плексных чисел, как пар |
a |
, данное в определении неудобно для счета – |
|
||
|
b |
|
оно требовалось для корректного и внятного определения новых объектов
без использования мистического символа |
|
−1 |
. |
Чаще всего используют традиционную алгебраическую z = a +bi или |
|||
тригонометрическую z = r(cosφ +isinφ) |
формы записи. Позже мы введем |
||
еще одну ─ показательную (экспоненциальную) форму представления.
Сложение (вычитание) просто осуществить в |
традиционной форме |
(a +bi) + (c + di) = (a + c) + (b + d)i . |
|
Произведение двух комплексных чисел (a +bi) |
(c + di) производится |
как умножение над обычными двучленами, а затем в итоговом результате надо выражение «i2 » заменить на « –1 ».
(1+ 2i)(2 −3i) =1 2 + 4i −1 3i −6i2 = 2 +i + 6 =8 +i .
Деление обычно осуществляется путем домножения |
|
на сопряженное |
|||||||||||
знаменателя |
2 +i |
= |
(2 +i)(3 +i) |
= |
6 +3i−1 + 2i +i2 |
= |
5 +5i |
= |
1 |
+ |
1 |
i . |
|
3 −i |
(3 −i)(3 +i) |
9 +1 |
10 |
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||||||
Возведение в степень уже становится громоздким. Прежде выясним, что происходит при возведении в степень мнимой единицы i :
i1 = i, i2 = −1, i3 = i2 i = −i, i4 = i2 i2 = (−1)(−1) =1, i5 = i4 i =i
Таким образом, идет чередование (i, −1, −i,1), (i, −1, −i,1)...
По соглашению считаем , что i0 =1.

Лекция № 15 Комплексные числа проф. Дымков М. П. 142
Извлечение квадратного корня: положим
a bi x yi a bi (x yi)2 x2 2xyi y2i2
(x2 y2 ) (2xy)i 10 a x2 y2 x, y.b 2xy
Эти формулы показывают, что операции умножения, деления, возведения в степень, извлечения квадратного корня – громоздки. Поэтому для упрощения обычно используют тригонометрическую форму записи комплексных чисел.
Умножение: r1(cos 1 isin 1) r2 (cos 2 isin 2 ) r1 r2 (cos( 1 2 )) .
Возведение комплексного числа в целую степень:
(r(cos isin ))n rn (cos n isin n ) при r 1 следует известная формула
Муавра |
(cos isin )n cos n isin n . |
|
|
|
|
|||||
Деление: |
очевидно |
r1(cos 1 |
isin 1) |
|
r1 |
(cos( |
2 |
) isin( |
2 |
)) . |
|
|
|
||||||||
|
|
r2 (cos 2 |
isin 2 ) |
1 |
1 |
|
||||
|
|
|
r2 |
|
|
|
|
|||
Извлечение корня (натуральной степени) из комплексного числа |
n z . |
|||||||||
Пусть z r(cos isin ) . |
|
|
|
|
|
|
|
|
||
Тогда можно показать, что n z имеет ровно « n » штук различных значений:
|
2k |
isin |
2k |
, где |
k 0,1, 2, ..., n 1. |
|
n z n r cos |
n |
n |
|
|||
|
|
|
|
|
||
Отметим, что если k заставить принимать больше значений, то пойдет «повторение» уже найденных чисел.
Например n 1 cos (2k 1) |
isin |
(2k 1) , k 0,1, 2, ..., n 1. |
|
|
|||||||||||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
k 0 |
|
|
|
isin |
|
i |
|
перемножая |
-1 1 |
1 |
|||
|
|
n 1 cos |
2 |
2 |
|||||||||||
n 2 |
|
|
|
|
|
|
|
|
комбинации |
|
|
||||
|
k 0 |
3 |
|
|
3 |
возможны 4 |
1 |
||||||||
|
|
isin |
i |
|
|
|
|
|
|
||||||
|
|
1 cos |
2 |
|
2 |
см. введение |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6. Экспонента с комплексной переменной
Имеет место следующая формула Эйлера (возведение в мнимую степень)

Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 143 |
|
|
|
|
|
eiφ = cosφ +isinφ – формула Эйлера
Строгое обоснование этой формулы можем получить из соотношения
|
|
z n |
|
ez = lim 1 |
+ |
|
. |
|
|||
z→∞ |
|
n |
|
Отсюда следует (см. также тригонометрическую форму записи), что для записи комплексных чисел можно использовать так называемую показательную форму записи
z = reiφ .
Тогда, например, умножение чисел легко реализуемо как z1 z2 = r1eiφ1 r2eiφ2 = r1 r2ei(φ1+φ2 ) .
Аналогично, деление чисел z1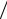 z2 = r1eiφ1
z2 = r1eiφ1 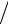 r2eiφ2 = r1
r2eiφ2 = r1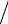 r2ei(φ1−φ2 )
r2ei(φ1−φ2 )
Определим экспоненциальную функцию с произвольным комплексным
параметром |
λ =α +iβ следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
eλx = e(α+iβ)x = eαxeiβx = eαx (cos βx +isin βx) . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Функция |
|
eλx |
|
обладает всеми свойствами, |
|
которые справедливы для веще- |
|||||||||||||||||||||||||||||||||||||
ственных чисел λ R : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
λ x |
λ x |
= e |
(λ |
+λ |
)x |
; 2) |
(e |
λx |
) |
' |
= λe |
λx |
; 3) ∫e |
λx |
dx = |
1 |
e |
λx |
+ e, λ ≠ 0. |
|
|
||||||||||||||||||||||
1) e 1 |
e |
2 |
1 |
2 |
|
|
|
|
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача. |
Найти вещественное решение уравнения |
|
cos |
|
= 5. |
|
|
|
|||||||||||||||||||||||||||||||||||
|
x |
|
|
||||||||||||||||||||||||||||||||||||||||
Из формулы Эйлера следует |
|
|
cos z = |
eiz +e−iz |
, z Ω. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei |
|
|
+e−i |
|
|
|
|||
Поэтому |
данное уравнение |
|
можно |
|
записать |
в |
виде |
x |
x |
|
= 5 или |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y = ei |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
y + |
−10 = 0 , |
|
где |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда находим, что ei |
|
=5 ± 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
x |
|
|
|
, |
|
то есть |
|
i |
|
|
= ln(5 ± 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
6 |
|
|
|
x |
6) |
|
|
|
||||||||||||||||||||||||||||||||||
или окончательно |
x = −ln2 (5 ± 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
6) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Тригонометрические функции комплексной переменной z C можно ввести, опираясь на формулы Эйлера:
cos z = |
eiz |
+ e−iz |
, |
sin z = |
eiz −e−iz |
, |
|
2 |
2i |
||||
|
|
|
|
|
||
Остальные обычным образом |
|
|
|
|
|
|
tg z = sin z |
, |
ctg z = cos z |
|
|||
|
|
cos z |
|
|
sin z |
|
Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 144 |
|
|
|
|
|
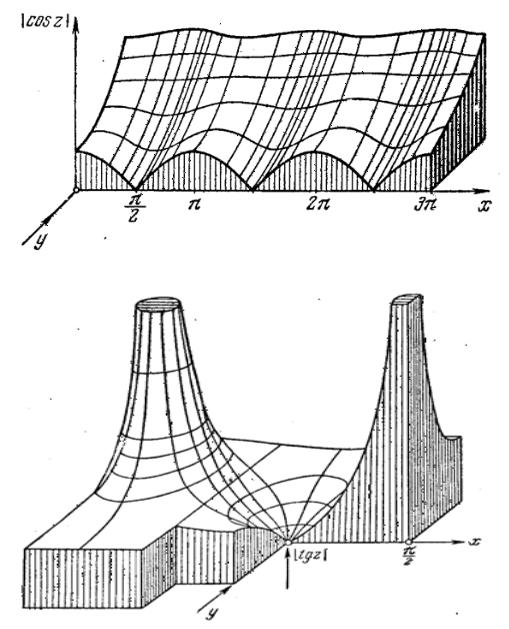
Графики некоторых тригонометрических функций:
Замечание.
Делались неоднократные попытки сделать и другие обобщения действительных и комплексных чисел (Гамильтон). Наиболее известными являются так называемые квантернионы, которые имеют четыре «единицы» 1, i, j, k, для которых имеется своя «арифметика». Эти числа находят применение, например, при описании вращений четырехмерного пространств, широко используемых в квантовой физике. Отметим, что иные такого рода «безконфликтные» обобщения (например, в виде триплетов) невозможны.
