
- •Векторы и операции над ними
- •Понятие n-мерного векторного пространства
- •Скалярное произведение векторов
- •Угол между n-мерными векторами
- •Линейная зависимость векторов
- •Базис и ранг системы векторов
- •Ортонормированный базис
- •Матрицы. Основные понятия
- •Операции над матрицами
- •Определитель матрицы
- •Обратная матрица
- •Ранг матрицы
- •Линейное уравнение. Основные понятия
- •Системы линейных уравнений
- •Теорема Кронекера-Капелли
- •Метод обратной матрицы. Метод Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы уравнений
- •Собственные векторы и собственные числа
- •Использование алгебры матриц
- •Использование систем линейных уравнений
- •Системы координат на плоскости
- •Связь полярной и прямоугольной систем координат
- •Простейшие приложения метода координат на плоскости
- •Линии на плоскости. Основные понятия
- •Общее уравнение прямой
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой L, проходящей через две заданные точки
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Общее уравнение плоскости
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •Точки пересечения прямой и плоскости
- •Понятие числовой последовательности. Арифметические операции над последовательностями
- •Связь бесконечно больших и бесконечно малых последовательностей
- •Простейшие свойства бесконечно малых последовательностей
- •Свойства сходящихся последовательностей
- •Монотонные последовательности
- •Предел функции
- •Односторонние пределы
- •Свойства пределов функций
- •Сравнение функций
- •Непрерывность функции в точке
- •Свойства непрерывных функций
- •Односторонняя непрерывность. Точки разрыва и их классификация
- •Свойства непрерывных на отрезке функций
- •Определение производной и ее простейшие свойства
- •Геометрический смысл производной
- •О связи дифференцируемости и непрерывности функций
- •Логарифмическая производная
- •Таблица производных простейших элементарных функций
- •Производные высших порядков
- •Геометрический смысл дифференциала
- •Применение производной в экономике
- •Теорема Ферма (о равенстве нулю производной)
- •Сравнение функций по скорости роста
- •Формулы Маклорена и Тейлора
- •Разложение в ряд Маклорена элементарных функций
- •Условия возрастания и убывания функции
- •Понятие экстремума
- •Необходимое условие экстремума
- •Выпуклость функции. Точки перегиба
- •Схема исследования функции на выпуклость
- •Асимптоты графика функции
- •Исследование функций и построение их графиков
- •Эластичность функции
- •Свойства эластичности функции
- •Эластичность элементарных функций
- •Определение комплексных чисел
- •Традиционная форма записи комплексных чисел
- •Геометрическое изображение комплексных чисел
- •Операции над комплексными числами
- •Экспонента с комплексной переменной
Лекция № 6 |
Прямая на плоскости |
|
|
|
|
проф. Дымков М.П. |
54 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Общее уравнение прямой
Уравнение прямой с угловым коэффициентом
Уравнение прямой с заданным угловым коэффициентом k и проходящей через заданную точку M0 (x0; y0 ).
Уравнение прямой L, проходящей через две заданные точки
Угол между двумя прямыми. Условия перпендикулярности и параллельности двух прямых
Уравнение прямой в отрезках
Нормальное уравнение прямой (нормированное уравнение прямой)
Расстояние от точки до прямой
Прямую на плоскости относительно фиксированной системы координат можно задать:
1)двумя различными ее точками;
2)точкой и направлением (вектором) прямой;
3)точкой прямой и вектором, перпендикулярным прямой.
Рассмотрим различные варианты аналитического задания прямой на плоскости.
1. Общее уравнение прямой
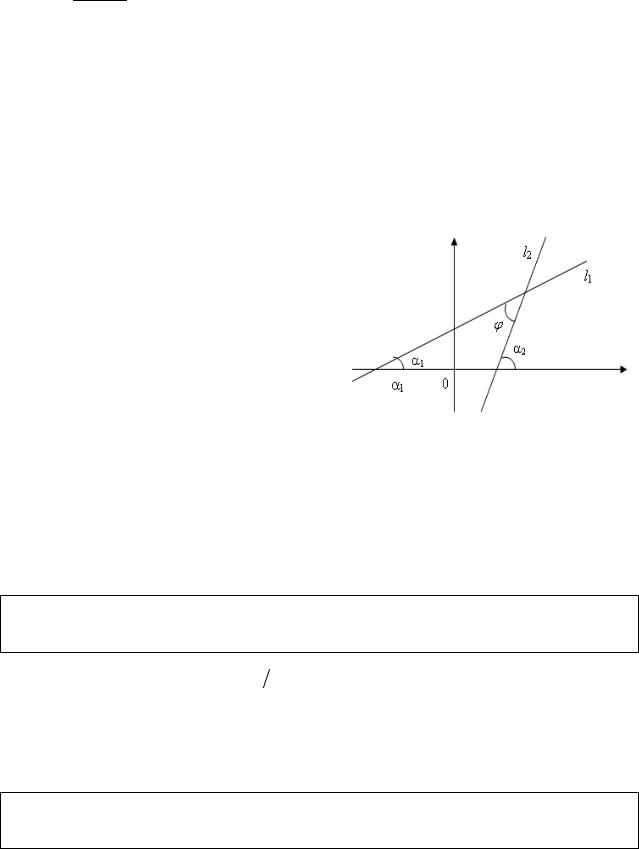
Пусть в прямоугольной системе координат Oху заданы вектор n(А; В)и точка
M0 (x0; y0 ).
Задача. Найти уравнение прямой L, проходящей через М0 и которая перпендикулярна вектору n.
Пусть М (х, у) − произвольная (текущая)
точка искомой прямой L. Тогда при любом положении точки М вектор M0M (x − x0, y − y0 ) должен быть вектору n (А; В). Следовательно, их скалярное произведение равно нулю:
( |
|
, |
|
)= − 0это векторное уравнение прямой. |
(1) |
M0M |
n |
Запишем (1) в координатной форме, пользуясь определением скалярного произведения:
|
|
A(x − x0 )+ B(y − y0 )= 0 |
(2) |
|
|
или |
|
|
|
|
|
|
Ax + By +C = 0 |
(3) |
где |
C = −Ax − By , |
A2 + B2 0≠ . |
|
|
|
0 |
0 |
|
|

Лекция № 6 |
Прямая на плоскости |
проф. Дымков М.П. |
55 |
Таким образом, показали, что координаты любой точки прямой L должны удовлетворять уравнению первой степени (3). Можно доказать и обратной: всякое уравнение (3) первой степени (относительно переменных х и у) определяет на
плоскости R2 некоторую прямую (перпендикулярную вектору n (А; В)). Уравнение (2) называют уравнением прямой, проходящей через дан-
ную точку перпендикулярно к данному вектору. Уравнение (3) называют общим уравнением прямой.
2. Уравнение прямой с угловым коэффициентом
Под углом наклона прямой к оси 0х понимают угол, отсчитываемый в направлении движения, противоположным движению часовой стрелки, от положительного направления оси х до данной прямой.
Тангенс угла наклона прямой к оси 0х называется угловым коэффициентом этой прямой и обозначается k.
1.Если прямая оси 0х, то k = 0. Если прямая оси 0х, то k не существует (обращается в ).
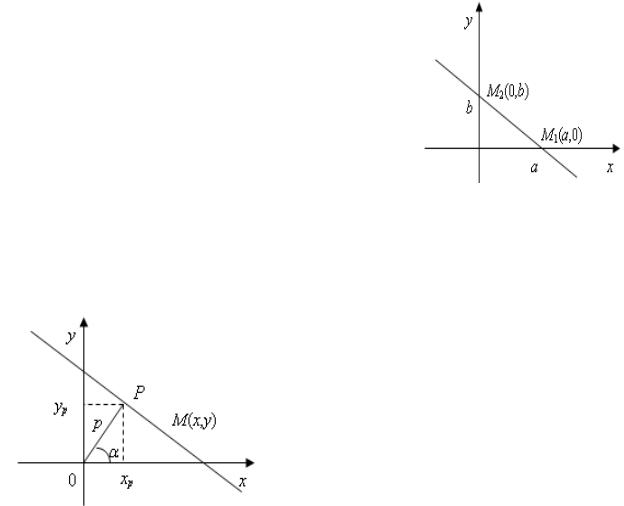
2.Если известен угловой ко-
эффициент k и величина b отрезка, отсекаемого прямой на оси 0у, то к ак следует из рисунка, для произвольной
точки М |
(х, у) |
этой прямой |
|||
NM |
= tgα |
k = |
y −b |
. Откуда |
|
BN |
x |
||||
|
|
|
|||
|
|
y = kx +b |
(4) |
||
(4) – уравнение прямой с угловым коэффициентом.
3. Уравнение прямой с заданным угловым коэффициентом k и проходящей через заданную точку M0 (x0; y0 )
Искомое уравнение L имеет вид y = kx +b . Но так как M0 L, то ее координаты удовлетворяют данному уравнению. Значит, y0 = kx0 +b . Вычитая это из предыдущего уравнения, имеем y − y0 = k (x − x0 ).
4. Уравнение прямой L, проходящей через две заданные точки
Пусть заданы M1 (x1; y1 ) и M2 (x2; y2 ), причем x1 ≠ x2 . Т.к. M1 L , то L имеет вид (см. выше) y − y1 = k (x − x1 ). Но этой же прямой должна принадлежать и
точка M2 . Следовательно, M2 удовлетворяет последнему уравнению: y − y1 = k (x − x1 ) y2 − y1 = k (x2 − x1 ). Отсюда k = (y2 − y1 ) (x2 − x1 ). Под-
(x2 − x1 ). Под-
Лекция № 6 |
Прямая на плоскости |
проф. Дымков М.П. |
56 |
ставляя найденный коэффициент в уравнение
y − y1 = y2 − y1 (x − x1 ). Если разделим на (y2 − y1) x2 − x1
имеем в итоге
y − y1 |
= |
x − x1 |
. |
|||
|
||||||
y |
2 |
− y |
|
x |
− x |
|
|
1 |
|
2 |
1 |
|
|
y − y1 = k (x − x1 ) имеем
(при условии y2 ≠ y1), то
5. Угол между двумя прямыми. Условия перпендикулярности и параллельности двух прямых
Определение. Углом между двумя прямыми (см. Рис.) называется любой из двух углов, образованных прямыми при их пересечении.
Пусть |
φ (0 ≤φ ≤π ) −угол |
|
между |
|
|
|
|||
прямыми l1 |
и l2 , которые задаются |
урав- |
|
|
|
||||
нениями y = k1x +b1 и y = k2x +b2 , соот- |
|
|
|
||||||
ветственно, где k1 = tgα1 и k2 = tgα2 . То- |
|
|
|
||||||
гда из рис. видно, что α2 =α1 +φ . Откуда |
|
|
|
||||||
φ =α2 −α1. |
Тогда, пользуясь формулами |
|
|
|
|||||
тригонометрии, имеем |
|
|
|
|
|
|
|
|
|
|
tgφ = tg(α |
2 |
−α )= |
tgα2 − tgα1 |
. |
||||
|
|
||||||||
|
|
|
1 |
|
|
1+ tgα1 |
tgα2 |
||
|
|
|
|
|
|
|
|||
Или |
tgφ = |
|
k2 − k1 |
|
|
|
(*) |
||
1+ k k |
2 |
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
Если прямые , то φ = 0 и tgφ = 0 k2 − k1 = 0 , т.е. k1 = k2 . И наоборот, если k2 = k1 , то φ = 0, т.е. прямые .
Таким образом, необходимым и достаточным условием параллельности двух прямых является условие k2 = k1 − равенство угловых коэффициентов.
Если прямые , т.е. φ =π 2 |
, то α |
2 |
= |
π +α |
|
tgα |
2 |
= tg |
π |
+α |
|
= |
||
|
|
|
2 |
1 |
|
|
|
|
2 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−ctgα = − |
1 |
, т.е. k |
2 |
= − |
1 |
или k |
2 |
k |
= −1 |
. И наоборот: если k |
2 |
k = −1, то |
|
|
|||||||||||
1 |
tgα1 |
|
|
k1 |
|
1 |
|
|
1 |
|||
|
|
|
|
|
|
|
|
|
|
|
из формулы (*) следует φ =π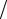 2, то есть прямые перпендикулярны.
2, то есть прямые перпендикулярны.
Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы выполнялось равенство k2 = −1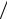 k1 (или k2 k1 = −1)
k1 (или k2 k1 = −1)
т.е. угловые коэффициенты взаимо-обратны с противоположным знаком.
Лекция № 6 |
Прямая на плоскости |
проф. Дымков М.П. |
57 |
6. Уравнение прямой в отрезках
Пусть прямая отсекает на осях координат Oх и Oу отрезки a ≠ 0 , b ≠ 0 , соответственно. Тогда легко видеть, что точки пересечения прямой с осями координат есть
M1 (a; 0), M2 (0;b). Составим теперь уравнение прямой, проходящей через данные точки пересечения M1 (a; 0), M2 (0;b).
Имеем |
y −0 |
= |
x |
− a |
или |
x |
+ |
y |
=1 |
b −0 |
|
− a |
a |
b |
|||||
|
0 |
|
|
|
|||||
─ уравнение прямой в отрезках.
7. Нормальное уравнение прямой (нормированное уравнение прямой)
Пусть на прямую (не проходящую через О), опущен перпендикуляр ОР, дли-
на которого |
р, а угол с |
осью 0х |
равен α. Из |
рис. |
xp = p cosα , |
|||||||||||
|
|
|
|
|
|
yp = p sinα . Возьмем точку M (x, y) на |
||||||||||
|
|
|
|
|
|
прямой. Т.к. прямые ОР и РМ взаимно- |
||||||||||
|
|
|
|
|
|
перпендикулярны, то |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
kOP kPM = −1. |
||||||||
|
|
|
|
|
|
Но k |
OP |
= tgα = sinα |
, k |
PM |
= |
yM − yP |
, |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
cosα |
|
|
|
xM − xP |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
(см. вывод уравнения прямой через две |
||||||||||
|
|
|
|
|
|
точки!), т.е. kPM = |
|
y − p sinα |
. |
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x − p cosα |
||||||
Тогда, подставляя найденное значение в равенство kOP kPM = −1, имеем |
||||||||||||||||
sinα |
|
y − p sinα |
= −1 |
или |
y sinα − psin2 α − pcos2 α + xcosα = 0. |
|||||||||||
cosα |
|
|||||||||||||||
|
x − p cosα |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда в итоге получим |
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
cosα + y |
sinα − p = |
0 |
─ нормальное уравнение прямой. |
||||||||||||
Для него характерно:
1)сумма квадратов коэффициентов при переменных х и у равна 1;
2)свободный член (− р) – отрицателен.
Пусть дано общее уравнение прямой Ax + By +C = 0 и для этой же прямой – ее нормальное уравнение x cosα + ysinα − p = 0 . Т.к. эти уравнения
