Эластичность функции y = f (x) можно найти из графика этой функции.

© БГЭУ Лекция № 13-14 Исследование функций с помощью производных проф. Дымков М. П. 129

5. Эластичность суммы функций u = u(x) и v = v(x) равна сумме их эластичностей, взятых с соответствующими весами:

Ex (u + v) = u u+ v Ex (u) + u +v v Ex (v) .

Эластичность элементарных функций

Вычислим эластичности некоторых функций.

Функция в зависимости от величины своей эластичности может быть

Эластичность функций применяется, например, при анализе спроса и потребления, в процессе анализа проектных рисков в ходе исследования изменений критериев оценки проектной эффективности в зависимости от изменений факторов риска.

Так, эластичность спроса Q по цене P EP (Q) = QP dQdP

показывает величину относительного изменения спроса на какой-либо товар при изменении цены этого товара. Она характеризует «чувствительность» потребителей к изменению цен на продукцию.

Вопросы для повторения

1.Сформулировать и доказать теорему о производной монотонной функции.

2.Сформулировать определение локального максимума и минимума функции.

3.Сформулировать и доказать теорему о необходимом условии экстремума.

4.Сформулировать и доказать теорему о первом достаточном условии экстремума.

5.Сформулировать и доказать теорему о втором достаточном условии экстремума.

6.Привести схему исследования функции на экстремум.

7.Сформулировать определение наибольшего и наименьшего значения функции.

8.Сформулировать определение выпуклости функции.

9.Сформулировать и доказать теорему об условиях направленности выпуклости функции вверх или вниз.

10.Дать определение точки перегиба и сформулировать необходимое и достаточное условия существования точки перегиба.

11.Привести определения вертикальной, горизонтальной и наклонной асимптот графика функции.

12.Привести схему полного исследования функции с целью построения ее графика.

13.Сформулировать определение эластичности функции, дать геометрическую интерпретацию.

14.Перечислить и доказать свойства эластичности функции.

Лекция № 15 Комплексные числа проф. Дымков М. П. 131

«КОМПЛЕКСНЫЕ ЧИСЛА»

« Число в математике, как и время в физике, известно каждому, но непонятно лишь специалистам».

Из истории чисел. Понятие числа складывалось в математике постепенно с развитием общества, а также под давлением как практики, так и внутренних потребностей самой математической науки. Можно не останавливаться на подробностях числовых множеств N Z Q (натуральных, целых, рацио-

нальных чисел) – их появление и становление имеет очевидную практическую востребованность. (! Заметим лишь, что введение отрицательных чисел можно интерпретировать как необходимость решения уравнения x + n = 0,n N , а потребность рациональных чисел – для решения уравнений mx + n = 0, m,n N .)

Переход (Q → R ) от рациональных чисел к действительным вызван

скорее внутренней логикой развития математики, чем практическими потребностями. В частности, к необходимости введения действительных чисел привело известное математическое открытие, вытекающее из теоремы Пифагора и состоящее в том, что диагональ единичного квадрата несоизмерима с

! Заметим, что для чисто практических целей рациональных чисел вполне хватает, так как с их помощью можно с любой наперед заданной точ-

следовательностей из таких чисел) относят к действительным (вещественным) числам. Эти числа как бы заполняют промежутки между рациональными числами. Этот факт очень важен для математики, так как действительные числа представляют собой ту непрерывную среду, в которой помещены рациональные числа, и где становится совершенно ясным, что для чисел характерно не только наличие действий сложения (! имеется трудность, например, сложения чисел с непериодическими дробями – как сложить бесконечные «хвосты» – в арифметике оперируют лишь с конечными числами), умноже-

ния, деления, но также неарифметическая операция предельного перехода.

Конечно же, та «непрерывная» среда, куда «затолкали» (обманули, вклеили, и т.п.) рациональные числа, содержит много тайн. Например, если сравнивать «количество» элементов этих множеств (как говорят еще, сравнивать мощности этих множеств), то оказывается, что множество действительных чисел R, «больше» (мощнее), чем другие множества N, Q, чисел (хотя

их тоже бесконечно много). Среди парадоксов бесконечных множеств, например, следующее: все множество и его часть (подмножество) имеют одинаковое «количество» элементов –{10,11,12,....} N .

Про множество N натуральных чисел говорят, что оно счетно. Можно доказать, что Z и Q в некотором смысле эквиваленты множеству N, т.е. имеют одну и ту же мощность (т.е. являются счетными). Множество же R не является счетным, оно «больше». Про множество R говорят, что оно имеет

мощность континуума.

! Интересно заметить, что множество R и его подмножество – например, интервал (0,1) ) – имеют одну и ту же мощность континуума.

Для сравнения мощностей находят так называемые кардинальные числа. Тогда факт, что R больше Q записывается card(R) > card(Q) .

Далее, множество иррациональных чисел тоже сложно устроено. Есть иррациональные алгебраические числа, т.е. это такие иррациональные числа,

которые являются корнем некоторого алгебраического многочлена (т.е. многочлена некоторой конечной степени с целыми коэффициентами). Множество алгебраических иррациональных чисел счетно. Остальные иррациональные числа, т.е. числа, которые не являются алгебраическими, называют трансцендентными числами. Так как множество R имеет мощность континуума, а все перечисленные его подмножества ( N,Q, множество алгебраи-

ческих чисел) имеют меньшую мощность (счетные), то следовательно множество иррациональных трансцендентных чисел самое большое из них и

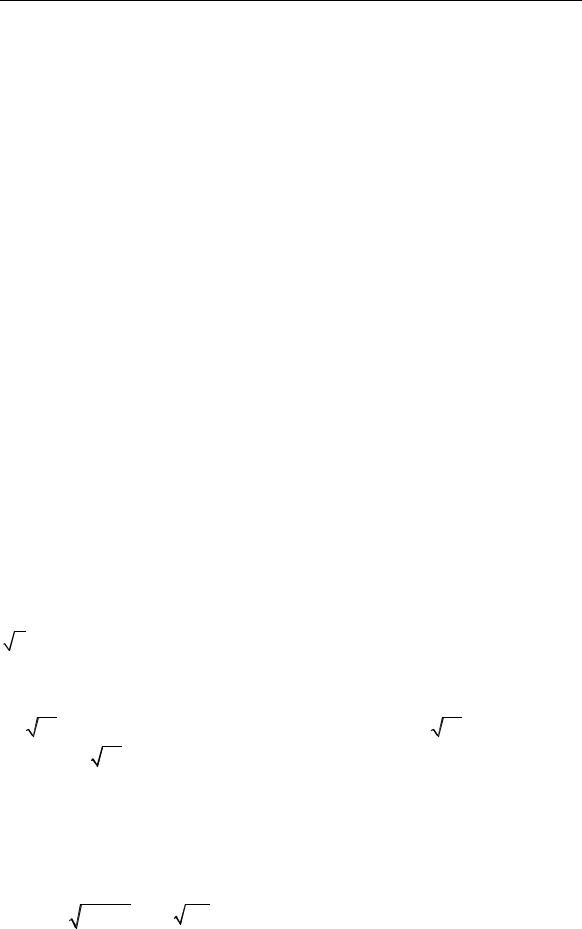
Лекция № 15 Комплексные числа проф. Дымков М. П. 133

имеет мощность континуума. Но, парадокс! Указать конкретно (предъявить) эти числа весьма непросто. (Чисел много больше, чем в N, а «показать» эти числа трудно!). Точнее, трудно доказать, что именно предъявленное число трансцендентно.

Примеры трансцендентности чисел. Совсем недавно доказали, что знаменитые числа «е» , «π »(Линдеман. 1882 г) являются трансцендентными (Напомним, что число «π »можно интерпретировать как отношение длины окружности к ее диаметру. Тогда с учетом трансцендентности числа «π » можно понять невозможность решения старинной задачи о квадратуре кру-

га). Числа вида αβ , где α алгебраическое, а β – иррациональное число, также является числом трансцендентным (Гельфонд, 1934).

! Любопытна так называемая « 7-ая проблема Гильберта»: Есть ли множества промежуточной мощности между «счетным» и « континуумом»? Была гипотеза, что нет таких множеств. В 1968 году Коэн (США) доказал неразрешимость этой проблемы, т.е. она не может быть не доказана, ни опровергнута (примерно ситуация как с «5-м пастулатом» Евклида).

Если теперь вернуться к 1-ой фразе в начале лекции, то должно быть ясно слушателям, что, действительно, числа (как математический объект) вещь далеко не тривиальная.

Перейдем теперь к очередному расширению, теперь уже расширению множества действительных чисел R →C .

Подобно тому, как в ситуации, когда алгебраическое уравнение x2 = 2 не имело решения во множестве рациональных чисел Q, и тогда для «исправления» этой ситуации был введен «внешний» (относительно Q) символ

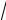2 и сделано расширение Q → R , путем добавления иррациональных чисел, так что это уравнение стало разрешимым в расширенном множестве. Точно так же для квадратного уравнения x2 = −1, можно ввести «внешний» символ

вое, «недействительное», число.

Нет такого действительного числа, квадрат которого равен «– 1»! Его называют «мнимой единицей». С помощью этого символа можно сделать

ные уравнения решаются. Но они, и арабские математики, которые много за-

нимались теорией уравнений, относились к этому спокойно – не все же на свете имеет решение!

Конечно, только возможность извлекать корень квадратный из отрицательного числа недостаточна, чтобы заводить в математике новые числа.

Впервые, по-видимому, мнимые величины появилось в трудах Кардано (1545), который искал выражения в радикалах для решений уравнений 3- ей и 4-ой степеней. (Заметим, что Абель доказал, что, вообще говоря, решения уравнений выше 4-ой степени не выражаются в радикалах.) Он счел их бесполезными и непригодными к употреблению. Действительно, недоверие к этим числам отразилось даже в названии «мнимое». Это недоверие усугублялось тем, что некритическое перенесение формул обычной алгебры на мни-

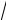−1 = i2 = −1 −1 = 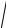(−1)2 = 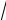1 =1. (Отметим наперед, что для комплексных

чисел нет понятия арифметического корня). Многие математики того времени изгоняли их, не признавали природы их, казалась им неясной, загадочной и даже мистической. Например, Ньютон не включал мнимые величины в понятие числа, Лейбниц ─ тоже, и ему принадлежит высокопарная фраза «Мнимые числа – это убежище божественного духа, почти что амфибия (гибрид) бытия и небытия».

Пользу мнимых величин впервые оценил Бомбелли (1572 г.). Он для записи решений кубических уравнений, которые имеют три действительных корня, использовал мнимые величины. Кроме того, дал описание основных операций над числами новой породы.

Термин «Комплексные числа» ввел Карно, но полное «гражданство» комплексным числам дал Гаусс. На протяжении 200 лет шли споры о природе комплексных чисел и само название «мнимые» числа отражало их нелегальный характер. Только на рубеже 18 – 19 веков Гаусс придал им полные гражданские права, дал им геометрическую интерпретацию, доказал основную теорему алгебры (любой многочлен имеет хотя бы один корень – действительный или комплексный). Комплексным числам предстоял долгий путь, прежде чем они стали ценнейшим математическим инструментом для решения важных прикладных задач в механике (упругость каркасов кораблей), физике (профили крыльев самолетов), гидродинамике ( обтекание препятствий).