Лекция №10 Предел функции. Непрерывность функций проф. Дымков М.П. 84
|
Пределы вида |
lim(1+ x)1x = e сводятся заменой |
y = |
1 |
к пределу |
|||
|
|
|
|
|
x→0 |
|
x |
|
|
|
1 |
y |
= e . |
|
|
|
|
lim 1 |
+ |
|
|
|
|
|
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x→∞ |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 x |
|
|
|
x |
|
|
|
|
|||
|
|
|
|
|
x + 2 |
|
|
2 |
|
|
2 |
|
2 |
|
||||||||||
Пример. 1) |
2 |
|
||||||||||||||||||||||
lim |
|
|
|
|
|
|
= lim 1+ |
|
|
= lim 1+ |
|
|
= y = |
|
|
→ |
||||||||
|
x |
|
|
x |
x |
|||||||||||||||||||
|
|
|
|
|
x→∞ |
|
|
|
|
x→∞ |
x |
|
|
|
|
|
||||||||
x |
|
1 |
|
|
|
|
1 |
|
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
= |
= lim |
(1+ y) y |
|
= lim(1+ y) y |
= e2.. |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
y |
y→0 |
|
|
|
|
|
|
y→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Некоторые другие важные пределы
|
|
1) |
lim |
loga (1 |
+ x) |
|
|
|
|
|
|
|
loga (1 |
+ x) |
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
= loga e a = e lim |
|
x |
|
= lne =1 . |
|
|||||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
|
|
|
x→0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
a |
x |
−1 |
|
|
|
e |
x |
−1 |
|
|
|
|
|
|
||||||
|
|
2) |
lim |
|
|
|
: lim |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
x |
= ln a a = e |
|
|
x |
=1 . |
|
|
|
|
|
|||||||||||
|
|
|
|
x→0 |
|
|
|
|
|
x→0 |
|
|
|
|
|
|
|
|
||||||||
|
|
3) lim (1+ x)α −1 =α . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x→0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнение функций |
|
|
|
|
|
|||||||
|
Рассмотрим бесконечно малые функции f (х) и g(х) в точке x0 , причем |
|||||||||||||||||||||||||
g(x) ≠ 0 в окрестности точки x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Определение. 1. |
Функция |
f (х) |
|
называют |
эквивалентной |
g(х) при |
|||||||||||||||||||
x → x |
|
, если |
lim |
f (x) |
= |
|
1 |
(f (х) g (х) при x → x ). |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
x→x0 g(x) |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример: sin x х, x → 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2. Говорят, |
что |
функции |
f (х) |
|
и |
g(х) при |
x → x0 |
одного |
порядка |
||||||||||||||||
малости, если lim |
|
f (x) |
|
= c, |
c ≠ 0, |
c ≠ ∞. |
|
|
|
|
|
|
|
|||||||||||||
|
g(x) |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Этот факт записывают иногда как (f (x) = O[g(x)]) и говорят, что функция
fесть «О-большое» от функции g
3.Говорят, что функция f (х) большего порядка малости, чем функция
g(х) при x → x , если |
lim |
f (x) |
= 0 . |
Этот факт записывают иногда как |
|
||||
0 |
x→x0 |
g(x) |
|
|
(f (x) = 0[g(x)]) и говорят, что функция |
f есть «о-малое» от функции g . |
|||
Лекция №10 |
Предел функции. Непрерывность функций |
проф. Дымков М.П. |
85 |
Можно проверить, что имеют место следующие эквивалентности:
1) |
x sin x tg x arcsin x arctg x (ex −1) ln(1+ x) при x → 0 ; |
||||
2) |
1−cos x ~ |
x2 |
при |
x → 0 ; и др. |
|
2 |
|||||
|
|
|
|
||
Эквивалентность функций может быть использована при вычислении пределов функций.
|
|
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
lim |
tg(x − 2) |
|
= lim |
|
x − 2 |
= lim |
|
x − 2 |
|
= lim |
|
1 |
= |
1 . |
|
|
|
|
|
|
|||||
x2 − 4 |
|
|
|
|
(x − 2)(x + 2) |
|
|
|
|
|
|
|
|
|||||||||||||
|
x→2 |
|
x→2 x2 − 4 |
x→2 |
|
|
x→2 x + 2 |
|
4 |
|
|
|
|
|
|
|||||||||||
|
|
|
ln(cos x) |
|
0 |
|
|
|
ln[1+ |
(cos x −1)] |
|
|
cos x |
−1 |
|
|
− |
x2 |
|
|
1 |
|
||||
2) |
lim |
|
= lim |
= lim |
= lim |
2 |
|
|
. |
|||||||||||||||||
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= − |
|
|||||||||||
|
x2 |
0 |
|
|
x2 |
x2 |
|
x2 |
|
2 |
||||||||||||||||
|
x→0 |
|
|
|
|
x→0 |
|
|
x→0 |
|
|
x→0 |
|
|
|
|||||||||||
3) |
lim arcsin16x = lim |
16x =8 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x→0 |
|
ln(1+ 2x |
|
x→0 |
2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
§3. Непрерывность функции в точке
Спределом функции тесно связано одно из важных понятий математического анализа – непрерывность функции (значительный вклад внесли Больцано, Коши).
Пусть функция y = f (x) является предельной точкой, принадлежащей множеству Х.
Определение 1. Функция y = f (x), x X называется непрерывной в точке x0 X , если она определена в самой точке x0 , а также в некоторой ее окрестности и справедливо следующее равенство
lim f (x) = f (x0 ) |
|
(1) |
|
x→0 |
|
|
|
т.е. существует предел функции в точке |
x0 и этот предел равен значению |
||
функции в этой точке. |
|
|
|
Символически (1) можно записать как |
lim f (x0 ) = f (lim x) , т.е. возможен |
||
|
x→0 |
x→x0 |
|
|
|
|
|
предельный переход под знаком функции. |
|
|
|
Определение непрерывности можно сформулировать на языке |
|||
последовательностей или на языке «ε–δ». |
|
|
|
Определение 2. Функция f (x) непрерывна в точке x0 , |
если для любой |
||
последовательности значений аргумента |
{xn}, сходящейся к |
x0 при n → ∞, |
|
Лекция №10 Предел функции. Непрерывность функций проф. Дымков М.П. 86
соответствующая последовательность значений функции {f (xn )} сходится к
числу A = f (x ). |
|
{x }→ x |
|
{f |
(x |
)}→ f (x |
) . |
|
|
||||||||
0 |
|
n n→∞ |
0 |
|
|
|
|
|
n |
|
|
n→∞ |
0 |
|
|
|
|
Определение |
3. |
Функция |
f (x) |
|
|
непрерывна |
в точке |
x0 , |
если |
||||||||
ε > 0 δ > 0, что для x , такого что |
|
x − x0 |
|
<δ |
выполняется неравенство |
||||||||||||
|
|
||||||||||||||||
|
|
|
f (x) − f (x0 ) |
|
<ε . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
Дадим еще одно определение непрерывности, эквивалентное |
|||||||||||||||||
определению 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
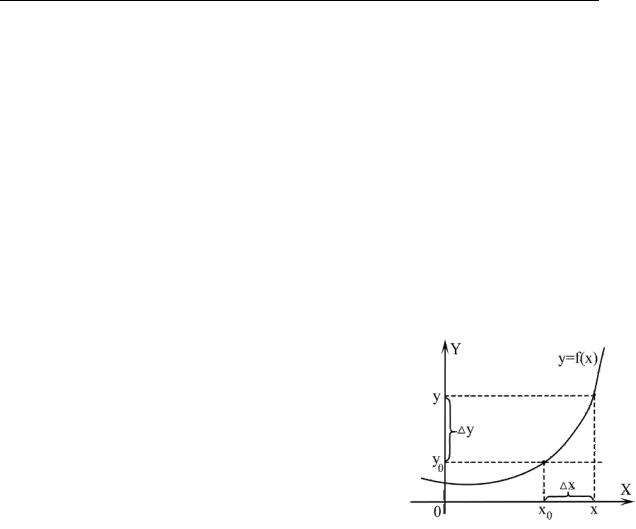
Разность ∆x = x − x0 −называют приращением аргумента в точке |
x0 , а |
||||||||||||||||
величину разности |
∆y = f (x) − f (x0 ) |
называют |
приращением |
функции, |
|||||||||||||
соответствующим приращению аргумента ∆x . |
|
|
|
|
|
|
|
||||||||||
Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆y = f (x) − f (x0 )= f (x0 + ∆x)− f (x) . |
|
|
|
|
|
|
|
|
|
|
|||||||
Тогда равенство (1) можно переписать в виде |
|
|
|
|
|||||||||||||
(перенося f (x0 ) и поднося его по знак «lim») |
|
|
|
|
|
|
|
||||||||||
lim [f (x) − f (x0 )]= 0 |
или |
lim ∆y = 0. |
|
|
|
|
|
|
|
||||||||
x→x0 |
|
|
|
∆x→0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, можно сформулировать
Определение 4. Функция f (x) называется непрерывной в точке x0 , если ее приращение в этой точке является бесконечно малой функцией при
∆x → 0 (x → x0 ) .
Из определения б.м.ф. :
Определение |
5. Функция f (x) непрерывна в точке x0 , |
если малое |
||||||||||||
приращение аргумента вызывает малое приращение функции, |
|
|||||||||||||
т.е. |
ε > 0 δ |
|
∆x |
|
<δ |
|
∆y |
|
<ε . |
|
|
|||
|
|
|
|
|
|
|||||||||
|
|
Свойства непрерывных функций |
|
|||||||||||
1. |
Если функции f (x) и |
|
g(x) непрерывны в точке x = x0 , |
то функции |
||||||||||
f (x) ± g(x), c f (x), |
(c −const, |
|
f (x) g(x), |
f (x) |
, |
(g(x ) ≠ 0) |
|
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
g(x) |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
являются также непрерывными в точке x = x0 .
Лекция №10 |
Предел функции. Непрерывность функций |
проф. Дымков М.П. 87 |
||
|
|
|
||
2. |
Непрерывность сложной функции. Если функция z =φ(x) непрерывна |
|||
в точке |
x = x0 , а функция y = f (z) непрерывна в точке z0 =φ(x0 ) , то тогда |
|||
сложная функция y = f (φ(x)) непрерывна в точке x = x0 . Это символически
записываю как lim |
f (ϕ(x)) = f |
|
|
lim |
ϕ(x) |
||
x→x0 |
|
x→x0 |
|
(т.е. «lim» можно переставлять под знаком непрерывной функции f.).
§ 4. Односторонняя непрерывность. Точки разрыва и их классификация
Определение. Функция y = f (x) называется непрерывной в точке x = x0 :
слева – если |
f (x0 −0)= |
lim |
f (x) = f (x0 ), |
|
|
|
f (x0 + 0)= |
x→x0 −0 |
f (x) = f (x0 ). |
справа – если |
lim |
|||
|
|
|
x→x0 +0 |
|
Отсюда следует, что непрерывность функции можно определить еще так: |
||||
функция f (x) |
непрерывна в точке x = x0 , если она определена в этой точке и ее |
|||
окрестности и |
f (x0 )= f (x0 −0)= f (x0 + 0) (т.е. является непрерывной, если она |
|||
одновременно непрерывна слева и справа). |
||||
Пусть функция |
f (x) определена в некоторой окрестности точки x0 , за |
|||
исключением, быть может, самой точки x0 .
Определение. Точка x0 называется точкой разрыва функции y = f (x),
если функция в этой точке не определена, или же не является в ней непрерывной [т.е. предел f (x) в точке x0 либо не существует, либо существует,
но не равен |
f (x0 ) !]. |
|
|
|
|
|
|
|
|
|
Дадим классификацию точек разрыва. |
|
|
||||||||
Определение. Точка |
x0 называется точкой разрыва I |
рода функции, |
||||||||
если в этой точке существуют |
f (x0 −0) и |
f (x0 + 0) , |
но f (x0 −0) ≠ f (x0 + 0). |
|||||||
При этом |
величина разности |
f (x0 + 0) − f (x0 −0) |
называется скачком |
|||||||
функции в точке x0 . |
|
|
|
|
|
|
|
|
|
|
Пример. y = sign x, |
y = |
|
x |
|
|
x . |
|
|
|
|
|
|
|
|
|
||||||
Определение. Точка x0 называется точкой устранимого разрыва, если |
||||||||||
f (x0 −0) = f (x0 + 0) ≠ f (x0 ) |
(либо f (x) |
не определена в |
точке x0 ). |
|||||||
Следовательно, чтобы устранить разрыв в точке x0 , достаточно положить f (x0 )= f (x0 0)= f (x0 + 0), т.е. надо изменить значение функции в одной
точке.