Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный экономический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lekcii.Vysshaya matematika (1 semestr).pdf

Скачиваний:

254

Добавлен:

20.02.2016

Размер:

2.06 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 105

Замечание 3. Иногда приходится применять правило Лопиталя последовательно несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми.

Пример 3. Найти lim ex .

x→∞ x5

Решение:

∞

lim

= lim

20x

x→∞ x

∞

x→∞ 5x

∞

x→∞

∞

x→∞ 60x

∞

= lim

∞

= lim

= +∞

120x

120

x→∞

∞

x→∞

Замечание

Хотя

правило

Лопиталя

работает только с

неопределенностями

∞

, неопределенности других типов могут быть

раскрыты

помощью

этого

правила,

если

путем

преобразований удастся

привести изучаемую неопределенность к типу

∞

или

∞

Пример 4.

Найти

lim

x sin

x→∞

Решение:

sin a

cos a

−a2

lim

x sin

[∞ 0]= lim

= lim

= a lim cos

= a

−1

x→∞

Сравнение функций по скорости роста

Рассмотрим некоторые функции, возрастающие при x → +∞. Составим из

них ряд

y = loga x,

a>1;

y = xk ,

k> 0;

y = ax ,

a>1;

y = x!;

y = xx

и докажем, что чем правее в ряду находится функция, тем быстрее она растет. Найдем пределы отношения во всех парах рядом стоящих функций при

x → +∞.

1)	lim
	x→+∞

loga x		правило			1	ln a		ln a
				lim	x		= lim		= 0 ,
	=		=
xk					kxk−1
		Лопиталя		x→+∞			x→+∞ kxk

следовательно, функция y = xk , k> 0, растет быстрее при x → +∞, чем y = loga x, a>1.

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 106

2)	lim	xk			правило		lim	kxk−1			.
				=		=
			x						x	ln a
	x→+∞ a				Лопиталя		x→+∞ a

Для любого k >1, в том ч исле и сколь угодно большого, справедливо неравенство n -1< k ≤ n , где n – натуральное число. Применив правило Лопиталя n раз, получим

lim	k(k −1)...(k − n +1)	,
x→+∞	ax lnn a xn−k

где величина n − k > 0 . Числитель дроби – постоянное число, знаменатель неограниченно возрастает, предел этой дроби равен нулю. Итак, функция y = ax , a>1 растет быстрее при x → +∞, чем y = xk , k >0 .

3) Найдем

lim

Аналогично случаю

2) для

любого

x→+∞ x!

неравенство n < a ≤ n +1. Запишем дробь следующим образом

x−n

...

n +1

где произведение последних

правильных

(x − n)

дробей

a >1 верно

заменено на

наибольшую из них в степени x − n .

x−n

<1.

Тогда

lim

≤

lim

= 0 , так как

n +1

x→+∞ x!

x→+∞ n!

n +1

n! x→+∞

n +1

С другой стороны, отношение

не может быть отрицательным. Итак, предел

рассматриваемого отношения функций ограничен сверху нулем и не может

быть меньше нуля. Поэтому

lim

= 0 .

x→+∞ x!

lim

= lim 1 2

...

= lim 1

lim 2 ...

lim

x→+∞ xx

x→+∞ x x

x→+∞ x

Первый

из

этих

пределов

lim

= 0 .

Величина

всех остальных

пределов

x→+∞ x

заключена между нулем и единицей. Следовательно, произведение этих

пределов есть нуль. Итак, xlim→+∞ xxx! = 0 . Функция y = xx самая быстрорастущая из перечисленных функций при x → +∞.

Формулы Маклорена и Тейлора

Эти формулы являются одними из основных формул математического анализа и имеют многочисленные приложения.

Рассмотрим многочлен n-й степени

P(x) = a0 + a1x + a2x2 +... + an xn .

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 107

Его можно представить в виде суммы степеней переменной х, взятых с некоторыми коэффициентами. Продифференцируем его n раз по х, найдем значения многочлена и его производных в точке x = 0, выразим из каждого полученного выражения коэффициенты a0,a1,...an , разместив результаты в трех

столбцах соответственно:

P(x) = a

+ a x + a x2 +... + a xn

P(0) = a0

a0 = P(0)

′

n−1

′

P (0)

P′(x)

= a

2a x +3a x

... + na x

P (0) = a1

′′

P′′(x)

= 2a

+3 2

a x... + n (n

−1)

a x

n−2

′′

P (0)

P (0) = 2 1 a2

′′′

P′′′(x) = 3 2

1 a ... + n (n −1)

(n − 2)

a x

n−3

′′′

P (0)

P (0) = 3 2 1 a3

……..

Вернемся к нашему многочлену, подставив вместо его коэффициентов

a0,a1,...an

выражения из 3-го столбца. Получим

′

′′

′′′

(n)

(0)

P(x) = P(0) +

(0)

+... +

Это

формула

Маклорена

для

многочлена

Р(х)

степени n.

Рассуждая

аналогичным образом, можно разложить многочлен Р(х) по степеням разности

(х − а) , где а – любое число.
Будем иметь
P(x) = P(a) +	P′(a)	(x − a) +		P′′(a)	(x − a)2 +...	+	P(n) (a)	(x − a)n .

1!			2!				n!		Р(х), или
Это выражение называется формулой Тейлора для						многочлена
разложением многочлена Р(х) по степеням (х − а) .
Пусть теперь в окрестности			точки х = 0 задана			функция			у = f (x), не

являющаяся многочленом, но имеющая в этой окрестности производные до n- го порядка включительно.

Вычислим величины f (0), f ′ (0),f ′′	(0),f	(n)
		... , и (0)зададим функцию

Q (x) = f (0) +

f ′(0)

x +

f ′′(0)

x2 +

f ′′′(0)

x3 +... +

f (n) (0)

xn .

Qn (x) есть многочлен степени

n. Он называется приближающим многочленом

для функции у = f (x) .

Если

бы

исходная

функция

у = f (x)

являлась

многочленом степени n, то выполнялось бы тождество f (x) ≡ Qn (x)

для всех

значений х из рассматриваемой окрестности. Поскольку это не так, положим f (x) = Qn (x) + Rn (x) ,

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 108

где Rn (x) называется остаточным членом. В курсе математического анализа

доказывается, что R (x) = o(xn ) .

Тогда формула разложения функции

f (x) в ряд по степеням х принимает вид:

′

′′

′′′

(n)

(0)

f (x) = f (0) +

(0)

x +

(0)

+... +

+ o(x

)

Эту формулу

называют формулой Маклорена разложения функции

f (x) по

степеням х

с остаточным членом в форме Пеано.

Для остаточного члена

получены выражения, позволяющие дать оценку его величине. Данная формула показывает, что, заменив f (x) в окрестности точки х = 0 приближающим

многочленом n-й степени, мы совершим ошибку, которая при x → 0 является бесконечно малой более высокого порядка, чем xn .

Проводя аналогичные рассуждения при разложении функции f (x) в окрестности точки x = a , получим формулу Тейлора

f (x) = f (a) +	f ′(a)	(x − a) +... +	f (n) (a)	(x − a)n + o((x − a)n ).
	1!		n!

Отсюда вывод: поведение любой n раз дифференцируемой функции в
окрестности точки	x = a	(в частности,		x = 0) можно описать

многочленом достаточно точно, а при n → +∞ – со сколь угодно высокой степенью точности.

Разложение в ряд Маклорена элементарных функций

Хотя формула Маклорена есть частный случай формулы Тейлора, в наших приложениях именно формула Маклорена будет определяющей. Формула Тейлора может быть приведена к формуле Маклорена подстановкой x - a = y .

Разложим в ряд Маклорена элементарные функции:

ex,; sinx

; xcos

; xln(1x +

), > -x1;

x(1+ )α ,

> -1.

С этой целью составим таблицу производных этих функций и значений

производных в точке x = 0.

′

′′

′′′

f (x)

f (0)

f (x)

f (0)

f (x)

f (0)

f (x)

ln(1+ x)

−

-1

1 2

(1+ x)2

(1+ x)3

1+ x

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 109

Подставляя в формулу Маклорена значения производных, взятые из

четных столбцов таблицы, получим разложения в ряд для каждой функции

ex =1+ x

+ x2

+ x3

+ o((x)3 ).

sin x = 0 +

1 x +

x2 +

−1 x3

x4 + o((x4 ))= x − x3

+ o((x4 )).

cos x =1+

−1 x2

0 x3

4 +

+ o((x5))

=1− x2

+ x4

+ o((x5))

ln(1+ x) = x − x2

+ x3

+ o((x3)).

(1+ x)α =1+ α x +

α(α −1) x2 + o((x2 ))

Замечание 1. Анализируя ряд разложения функции, легко заметить

закономерности образования ряда и выписать следующие члены разложения.

Пример 5. Разложить по формуле Маклорена функцию sin x .

Решение.

sin x

= x −

−

+... + (−1)

k−1 x2k−1

+...

(2k −1)!

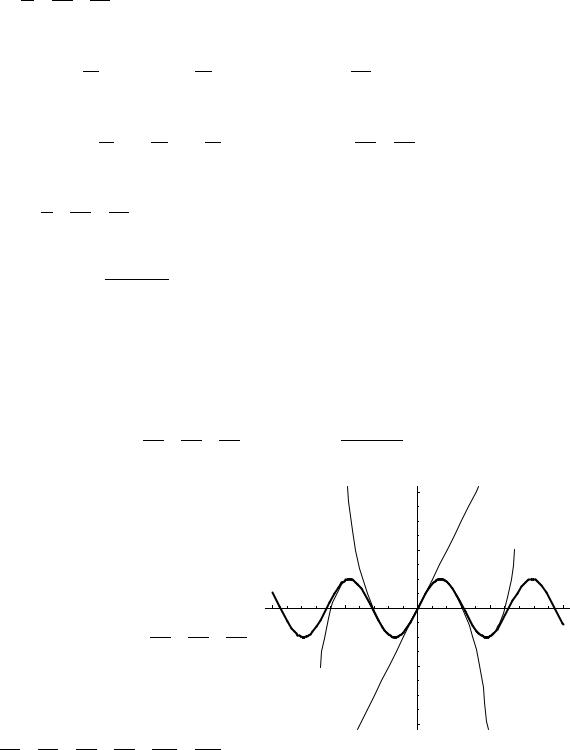
На

рисунке

изображен

жирной

линией

график

функции

Y1 = sin x ,

тонкими

линиями

его

приближение

одним членом ряда Маклорена

Y2 = x ,

приближение четырьмя

отличными от

нуля членами ряда Y

= x

−

-10

-5

-2

и, наконец, приближение

семью

членами ряда

Y = x − x3 + x5 − x7 + x9 − x11

+ x13 .

-4

11!

13!

Замечание 2. Эти формулы дают возможность производить разложения в

ряд некоторых функций без использования общей схемы с нахождением

производных высокого порядка.

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 110

Пример 6. Разложить по формуле Маклорена функцию e2x+1 до o((x4 )).

Решение. Разложим функцию e2x+1								в окрестности			х = 0 до o((x4 )).
Воспользуемся разложением функции ex								в ряд, заменив в правой части этого
ряда величину х на 2х :
	2x	+	(2x)	2	+ (3x)	3
e2x+1 = e1 1+							+ o((x4 )) =
	1!		2!		3!
		9	x3 + o				= e	+ 2ex + 2ex2 +	9	ex3	+ o((x4 ))
e 1+ 2x + 2x2 +		2			((x4 ))				2

Замечание 3. Ранее мы установили асимптотические формулы для некоторых элементарных функций, например, sin x = x + o(x) . Мы пользовались

ими при вычислении простейших пределов. Для нахождения некоторых более сложных пределов такого асимптотического приближения может оказаться недостаточно и следует брать следующие члены разложения.

Пример 7. Найти предел lim x −sin x .

x→0 x3

Решение. Если ограничиться разложением sin x = x + o(x) , то в пределе получается выражение:

lim	x −sin x	= lim	x −(x + o(x))	= lim	x o(1)	= lim o(1) .
	x3		x3		x3
x→0		x→0		x→0		x→0 x2

Чему равен такой предел, сказать невозможно. Неизвестно, какая бесконечно малая функция скрывается под о(1) . Поэтому правильное решение

выглядит так:

x − x −

+ o(x

)

+ o(x)

x −sin x

lim

= lim

x→0

Замечание 4. Если в разложении для функции (1+ x)α

положить α = n , где

n - натуральное число, то все члены этой формулы начиная с (n+1)-го исчезают, и формула Маклорена превращается в известную формулу бинома Ньютона

(1+ x)n =1+ n x + n(n −1) x2 +... + xn , 1! 2!

т.е. бином Ньютона является частным случаем разложения функции (1+ x)α в ряд Маклорена.

Лекция №12 Основные теоремы дифференциального исчисления проф. Дымков М.П. 111

Вопросы для повторения

1.Сформулировать и доказать теоремы Ферма, Ролля, Лагранжа и Коши.

2.В чем геометрический смысл теоремы Ролля?

3.Привести геометрический смысл теоремы Лагранжа.

4.Как в смысле общности соотносятся между собой теоремы Роля, Лагранжа и Коши?

5.Сформулировать и доказать правило Лопиталя при x → a .

6.Можно ли распространить правило Лопиталя на случай x → +∞? Как это обосновать?

7.На какие типы неопределенностей распространяется правило Лопиталя?

8.Провести сравнение степенной, показательной и логарифмической функций по скорости роста при x → +∞.

9.Назвать наиболее медленно растущую функцию из известных вам и наиболее быстро растущую при x → +∞.

10.Привести разложение многочлена n-й степени в ряд, используя формулу Маклорена.

11.Привести в общем виде формулы Тейлора и Маклорена разложения

функции в степенной ряд.
12.Получить	разложение	в	ряд	Маклорена	функций
ex , sinx , cosx	, ln(1x+ ), (1x+	)α .

13.Как соотносятся между собой асимптотические формулы и формула Маклорена разложения функции в степенной ряд?

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2122 / 2822 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019210.94 Кб5Lek-06-1C_8_2-ЗП.doc
#
24.09.2019117.76 Кб8Lek-07-1C_8_2-20.doc
#
24.09.201976.29 Кб7Lek-08-1C_8_2-80.doc
#
24.09.201994.72 Кб8Lek-09-1C_8_2-Свод.doc
#
24.09.2019441.34 Кб10Lek-10-Гал_8.10-Опис.doc
#
20.02.20162.06 Mб254Lekcii.Vysshaya matematika (1 semestr).pdf
#
20.02.20162.84 Mб456Lekcii.Vysshaya matematika (2 semestr).pdf
#
20.02.2016744.96 Кб58lekcii_marketingovye_issledovaniya.doc
#
20.02.2016610.3 Кб35lekcii_nac_ekonomika_rb.doc
#
20.02.2016645.12 Кб25lekcii_nac_ekonomika_rb.doc
#
20.02.201610.32 Mб234lekcii_po_makroekonomike.doc