пределов, либо хотя бы один из односторонних пределов является бесконечным.

2) y = sin 1x , x = 0 − II рода, т.к. lim sin 1x не существует ни справа, ни слева.

§ 5. Свойства непрерывных на отрезке функций

Определение. Функция f (x) называется непрерывной на [a,b], если она непрерывна в каждой точке x [a,b] этого отрезка (при этом в точке х = а непрерывна справа, а в точке х = b непрерывна слева).

определяем наибольшее значение.

Непрерывные функции обладают рядом замечательных свойств.

Теорема (первая теорема Вейерштрасса).

Непрерывная на отрезке [a,b] функция является ограниченной функцией.

Теорема (вторая теорема Вейерштрасса).

Непрерывная на отрезке [a,b] функция достигает на этом отрезке своего наибольшего и наименьшего значений (заметим, что точки, в которых достигают наибольшее и наименьшее значения не обязательно единственны).

Теорема (Больцано – Коши о промежуточном значении).

Понятие производной появилось в работах Лейбница, Ньютона, Лагранжа. Это понятие составляет основу дифференциального исчисления. К использованию производных приводят многие задачи по исследованию различных процессов, т.е. явлений, которым присущи изменения, что естественно для окружающего мира.

Задачи, приводящие к понятию производной.

Определение производной и ее простейшие свойства

Геометрический смысл производной

О связи дифференцируемости и непрерывности функций

Основные правила дифференцирования

Логарифмическая производная.

Дифференцирование сложных функций

Дифференцирование обратной функции

Дифференцирование неявных функций

Таблица производных основных элементарных функций

Производные высших порядков

Понятие дифференциала функции

Геометрический смысл дифференциала

Применение дифференциала в приближенных вычислениях

Применение производной в экономике

Эластичность функций

§1. Производная функции

1.Предварительные соображения. (Задачи, приводящие к понятию производной).

Кпонятию производной мы приходим всякий раз, когда требуется изучить скорость изменения, в том числе и в экономике – скорость роста, ускорение роста, темпы роста и др. Природу производной легче понять, если ее представить как скорость (так именно и поступил Ньютон).

а) Рассмотрим механическую задачу определения мгновенной скорости точки, движущейся прямолинейно с переменной скоростью.

Пусть s = s(t) −уравнение движения точки, т.е. зависимость пройденного

пути s от времени t. Пусть s0 = s(t0 ) −путь, пройденный точкой к моменту t = t0 , а s1 = s(t1) −путь, пройденный точкой до момента t1 = t0 + ∆t , где ∆t > 0 некоторая малое число. Тогда путь, пройденный за время ∆t = t1 −t0 равен s1 − s0 = s(t0 + ∆t)− s(t0 )= ∆s .

Так как скорость – переменная величина, то мы можем вычислить ее среднюю скорость за время ∆t : vcp. = ∆∆st −как отношение пройденного пути к

затраченному времени. Если бы точка двигалась с постоянной скоростью, то найденная средняя скорость была бы одинаковой на всем промежутке движения. Однако движения точки неравномерно, а значит, скорость точки непрерывно меняется. Во многих случаях надо знать скорость движения в разные моменты времени (например, с какой скоростью вылетевшая из ружья пуля долетает до человека (если скорость пули = 0, то пуля упадет, если скорость достаточно велики ≈ 300 м/сек., то человек упадет!)).

рость – это скорость за бесконечно малый промежуток.

Замечание. По физическому смыслу, при «безграничном уменьшении ∆t → 0 » заданный момент времени t0 есть не что иное как «нулевой промежу-

ток времени» ∆t = t1 −t0 = 0, но за «нулевой промежуток» времени точка, разу-

меется, проходит нулевое расстояние. Следовательно, если бы решили вычислять мгновенную скорость также как и среднюю скорость, т.е. деля пройденное

расстояние на требующееся для этого время, то получили бы выражение 00 , ко-

торое не имеет смысла. Выход был найден в построении последовательности средних скоростей, и определение той величины, к которой стремится эта последовательность.

б) Нахождение производительности труда. Пусть функция z = z(t) выра-

жает количество z произведенной рабочим продукции за время работы t. Вычислим количество произведенной продукции за время ∆t = t1 −t0 :

∆z = z(t1)− z(t0 )= z(t1 + ∆t)− z(t0 ).

то он называется производительностью труда рабочего в момент t0 .

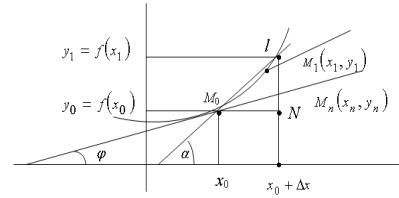
в) Геометрическая задача о проведении касательной к плоской кривой. Пусть y = f (x), x X −

непрерывная функция, график которой в декартовойсистеме координат Oху представляется кривой l.

Если M1 ≠ M0 , то прямая M0M1 (см. Рис.)

называется секущей.

Определение. Предельное положение секущей M0M1 , когда точка

Так как M1 → M0 эквивалентно ∆x → 0 , то угловой коэффициент касательной к кривой l получаем как предел (если он и конечен):

Функция, имеющая производную в точке x0 , называется дифференциро-

ванной в точке x0 .

Замечание. Определение дифференцируемости функций может быть дано следующим образом: Функция y = f (x) называется дифференцируемой в

точке x0 , если ее приращение в этой точке можно представить в виде

f (x0 + ∆x)− f (x0 )= A ∆x + o(∆x) , где А – постоянная, o(∆x) −бесконечно малая функция.

Оказывается, имеет место утверждение: Функция f (x) −дифференциру-

ема в точке x0 тогда и только тогда, когда для функции f в точке x0 существует конечная производная f ′(x0 ) (т.е. если A = f ′(x0 ) в предыдущей фор-

муле). Фактически, эту эквивалентность мы и использовали в приведенном определении.

Функция, дифференцируемая во всех точках множества Х, называется

дифференцируемой на Х.

Если в определении производной рассматриваются односторонние пределы, то получаем соответствующее определение левой и правой производной в