1. Параметрическое уравнение прямой

Пусть даны точка M0 (x0, y0, z0 ) на прямой и вектор s = (l,m,n) , лежащий на

этой прямой (или ей параллельной). Вектор s называют еще направляющим вектором прямой.

Этими условиями однозначно определяется прямая в пространстве. Найдем ее

уравнение. Возьмем произвольную точку M (x, y, z) на прямой. Ясно, что векторы

M0M (x − x0, y − y0, z − z0 ) и s коллинеарны.

Следовательно, M0M = t s − есть векторное уравнение прямой.

В координатной записи последнее уравнение имеет следующее параметрическое представление

двух углов, образованными двумя прямыми, соответственно параллельными данной и проходящими через одну точку (для чего возможно требуется совершить параллельный перенос одной из прямых).

Из определения следует, что один из углов равен углу ϕ между

Прямые перпендикулярны s1 s2 l1 l2 + m1 m2 + n1 n2 = 0 .

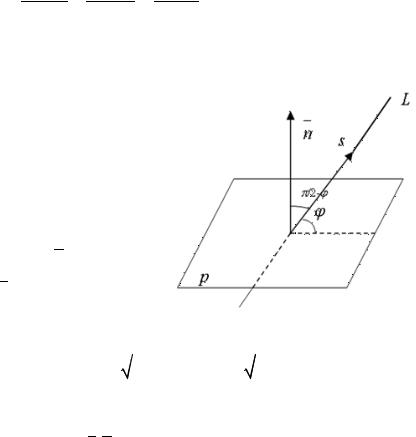
4.Угол между прямой и плоскостью. Условия « » и « » прямой и

плоскости

Пусть прямая L задана своим каноническим уравнением x −l x0 = y −my0 = z −nz0 ,

а плоскость P – уравнением

Ax + By +Cz + D = 0.

Определение. Углом между прямой L

и плоскостью р называется острый угол между прямой L и ее проекцией на плоскость.

Из определения (и рисунка) следует, что искомый угол ϕ является дополнительным (до прямого угла) к углу между вектором нормали n(A, B,C) и

направляющим вектором s(l,m,n) .

( . берется, чтобы получить острый угол).

Если L Р, то тогда s n (s,n)= 0

Теперь, если подставить найденное «t» в параметрические уравнения прямой, то найдем искомую точку пересечения

будем называть числовой последовательностью (или просто последовательностью).

Отдельные числа x3, x5, xn будем называть элементами или членами последовательности (1). Символ xn называют общим или n-м членом данной последовательности. Придавая значение n = 1, 2, … в общем члене xn мы получаем, соответственно, первый x1 , второй x2 и т.д. члены.

Последовательность считается заданной (см. Опр.), если указан способ получения любого ее элемента. Часто последовательность задают формулой для общего члена последовательности.

Для сокращения записи последовательность (1) иногда записывают как

Структура общего члена (его формула) может быть сложной. Например,

Иногда последовательность задается так называемыми рекуррентными формулами, т.е. формулами, позволяющими находить последующие члены последовательности по известным предыдущим.

Пример (числа Фибоначчи). Пусть x1 = x2 =1 и задана рекуррентная формула xn = xn−1 + xn−2 для n = 3, 4, … . Тогда имеем последовательность 1, 1,

2, 3, 5, 8, … (числа Леонардо из Пизы по прозвищу Фибоначчи). Геометрически числовую последовательность можно изобразить на чис-

ловой оси в виде последовательности точек, координаты которых равны соот-

ветствующим членам последовательности. Например, {xn}= 1n .

Лекция № 8-9 Основы математического анализа проф. Дымков М.П. 66

Рассмотрим наряду с последовательностью {xn} еще одну последовательность {yn}: y1, y2, , y,n (2).

Определение. Суммой (разностью, произведением, частным) последо-

вательностей {xn} и {yn} называется последовательность {zn}, члены кото-

Произведением последовательности {xn} на число c R называется последовательность {c xn}.

Определение. Последовательность {xn} называется ограниченной

сверху (снизу), если существует вещественное число М (m), такое что каждый элемент этой последовательности xn удовлетворяет неравен-

ству xn ≤ M (xn ≥ m). Последовательность называется ограниченной, если она ограничена и сверху и снизу m ≤ xn ≤ M . Последовательность xn называ-

ется неограниченной, если для положительного числа А (сколь угодно большего) найдется хотя бы один элемент последовательности xn , удовлетворя-

ющий неравенству xn > A.

Примеры.

{xn}={1n}−ограничена, т.к. 0 ≤ xn ≤1.

{xn}={n}−ограничена снизу 1, но является неограниченной.

{xn}={−n}−ограничена сверху (–1), но также неограниченная.

Определение. Последовательность {xn} называется бесконечно малой,

если для любого положительного вещественного числа ε (сколь бы малым его не взяли) существует номер N , зависящий, вообще говоря от ε, (N = N(ε)) такой, что при всех n ≥ N выполняется неравенство xn <ε .

Пример. {xn}= 1n .

Определение. Последовательность {xn} называется бесконечно боль-

шой, если для положительного вещественного числа А (какое бы большое оно не было) найдется номер N (N = N(A)) такой, что при всех n ≥ N выпол-

няется неравенство xn > A.