
- •Векторы и операции над ними
- •Понятие n-мерного векторного пространства
- •Скалярное произведение векторов
- •Угол между n-мерными векторами
- •Линейная зависимость векторов
- •Базис и ранг системы векторов
- •Ортонормированный базис
- •Матрицы. Основные понятия
- •Операции над матрицами
- •Определитель матрицы
- •Обратная матрица
- •Ранг матрицы
- •Линейное уравнение. Основные понятия
- •Системы линейных уравнений
- •Теорема Кронекера-Капелли
- •Метод обратной матрицы. Метод Крамера
- •Метод Гаусса решения систем линейных уравнений
- •Однородные системы уравнений
- •Собственные векторы и собственные числа
- •Использование алгебры матриц
- •Использование систем линейных уравнений
- •Системы координат на плоскости
- •Связь полярной и прямоугольной систем координат
- •Простейшие приложения метода координат на плоскости
- •Линии на плоскости. Основные понятия
- •Общее уравнение прямой
- •Уравнение прямой с угловым коэффициентом
- •Уравнение прямой L, проходящей через две заданные точки
- •Уравнение прямой в отрезках
- •Нормальное уравнение прямой
- •Расстояние от точки до прямой
- •Общее уравнение плоскости
- •Нормальное уравнение плоскости
- •Расстояние от точки до плоскости
- •Параметрическое уравнение прямой
- •Каноническое уравнение прямой
- •Точки пересечения прямой и плоскости
- •Понятие числовой последовательности. Арифметические операции над последовательностями
- •Связь бесконечно больших и бесконечно малых последовательностей
- •Простейшие свойства бесконечно малых последовательностей
- •Свойства сходящихся последовательностей
- •Монотонные последовательности
- •Предел функции
- •Односторонние пределы
- •Свойства пределов функций
- •Сравнение функций
- •Непрерывность функции в точке
- •Свойства непрерывных функций
- •Односторонняя непрерывность. Точки разрыва и их классификация
- •Свойства непрерывных на отрезке функций
- •Определение производной и ее простейшие свойства
- •Геометрический смысл производной
- •О связи дифференцируемости и непрерывности функций
- •Логарифмическая производная
- •Таблица производных простейших элементарных функций
- •Производные высших порядков
- •Геометрический смысл дифференциала
- •Применение производной в экономике
- •Теорема Ферма (о равенстве нулю производной)
- •Сравнение функций по скорости роста
- •Формулы Маклорена и Тейлора
- •Разложение в ряд Маклорена элементарных функций
- •Условия возрастания и убывания функции
- •Понятие экстремума
- •Необходимое условие экстремума
- •Выпуклость функции. Точки перегиба
- •Схема исследования функции на выпуклость
- •Асимптоты графика функции
- •Исследование функций и построение их графиков
- •Эластичность функции
- •Свойства эластичности функции
- •Эластичность элементарных функций
- •Определение комплексных чисел
- •Традиционная форма записи комплексных чисел
- •Геометрическое изображение комплексных чисел
- •Операции над комплексными числами
- •Экспонента с комплексной переменной
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УО «Белорусский государственный экономический университет»
М.П. Дымков
ВЫСШАЯ МАТЕМАТИКА Первый семестр
Курс лекций для студентов экономических
специальностей вузов
Минск 2014

Лекция №1 |
Векторы и операции над ними |
|
|
|
проф. Дымков М.П. |
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Векторы и операции над ними.
Понятие n-мерного векторного пространства
Скалярное произведение векторов
Угол между n-мерными векторами
Линейная зависимость векторов
Базис и ранг системы векторов
Ортонормированный базис
§1. Векторы и операции над ними.
Всвоей практической деятельности человек встречается с величинами различного рода. Одни из них, например, площадь, объем, масса, температура полностью характеризуются заданием своих численных значений. Такие величины называются скалярными. Другие же величины, например, сила, скорость, ускорение определяются не только своим числовым значением, но и направлением их действия. Такие величины называют векторными. При этом для анализа векторных величин с одинаковым успехом используют как геометрическую, так и алгебраическую формы их представления.
Вгеометрии вектором называют направленный отрезок. Геометрическое представление вектора на плоскости приводилось в школе, и поэтому не будем его здесь в деталях приводить.
Для алгебраического описания векторов их связывают с некоторой системой координат. В фиксированной системе координат, например, в плоскости
каждый вектор a определяется однозначно своими двумя координатами: a = (a1, a2 ); вектор в пространстве ─ тремя координатами: a = (a1, a2 a,3 ).
Замечание. При геометрическом изображении векторов часто используют понятие свободных и связанных векторов. Под связанным вектором понимают направленный отрезок прямой, у которого указано какой из концов является началом и концом. Длиной вектора называют расстояние (в выбранном масштабе) между конечными точками отрезка. Часто начало вектора не имеет значения, существенны лишь его длина и направление. Два вектора называют эквивалентными, если они имеют одинаковую длину и одинаково направлены (сонаправлены). Понятно, что если есть фиксированный связанный вектор, то ему соответствует бесконечно много эквивалентных ему связанных векторов. Все множество – это множество эквивалентных связанных векторов (пучок векторов) называют свободным вектором. Для задания свободного вектора достаточно задать какой-нибудь один его представитель, например, выходящий из

Лекция №1 Векторы и операции над ними проф. Дымков М.П. 2
начала координат. Тогда второй конец вектора однозначно определит единственную точку (a1, a2 a,3 )−конец вектора (здесь говорим о векторах в про-
странстве). И наоборот, задав точку (a1, a2 a,3 ), мы физически задаем вектор с началом в начале координат, а конец – (a1, a2 a,3 ).
Приведем теперь обобщение понятия вектора на произвольный n-мерный случай. Такое обобщение естественно и диктуется приложениями. Часто приходится изучать объекты, для задания которых недостаточно задать 2 или 3 координаты. Например, положение самолета определяется в пространстве заданном 3-х координат его центра масс, 2-мя углами описывающие направление оси самолета, угол поворота самолета вокруг его оси (углы атаки, тангажа) и др. Другой пример, пусть некоторое предприятие в своем производстве использует
n видов сырья. Тогда, если через |
xi , i =1,2,...,n |
обозначить количество сырья i- |
|||||||||||||
го вида, необходимое предприятию |
на одни |
сутки, то |
тогда набор чисел |
||||||||||||
(x1, x2, , |
xn ) означает все сырье, которое использует |
предприятие в своем |
|||||||||||||
производстве в течение суток. |
|
|
|
|
|
|
|
|
|||||||
|
Определение 1. Любой упорядоченный набор из n-действительных чисел |
||||||||||||||
(x , x , , |
x) |
называется n-мерным вектором и обозначается |
|
|
. Числа |
||||||||||
|
x |
||||||||||||||
1 |
2 |
n |
|
|
|
|
|
|
|
|
|||||
xi , |
i =1,..., n, составляющие упомянутый набор, называются компонентами |
||||||||||||||
(координатами) вектора |
|
. |
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|||||||
|
Часто вектор |
|
будем писать просто как |
x (для упрощения записей без |
|||||||||||
|
x |
||||||||||||||
черты сверху, если это не будет приводить к недоразумению) так, |
что возмож- |
||||||||||||||
на |
запись вектора в виде x = (x1, , |
xn ). |
|
|
|
|
|
||||||||
|
Координаты n-мерного вектора можно расположить либо в строку |
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x = (x , , |
|
), либо в столбец |
|
1 |
|
|
|
|
|
|
|||||
x |
x = |
. Иногда в литературе предписыва- |
|||||||||||||
|
1 |
n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
||
ют записывать n-мерный вектор как вектор столбец и тогда для того, чтобы записать в виде строки используют операцию транспонирования
x1 T
xT = x2 = (x1, x2 , xn ,).xn
Мы не будем следовать жесткому стилю обозначений.
|
|
|
Лекция №1 |
|
Векторы и операции над ними |
|
|
|
|
|
|
проф. Дымков М.П. |
|
3 |
|||||||||||||||
|
|
|
Определение 2. Два n-мерных вектора (т.е. два вектора с одним и тем |
||||||||||||||||||||||||||
же числом n координат) x = (x1, x2 , |
xn ,) |
и y = (y1, y2 , |
yn ,) |
равны, тогда |
|||||||||||||||||||||||||
и только |
тогда, |
когда |
равны |
их |
соответствующие |
координаты |
|||||||||||||||||||||||
|
x1 = y1, x2 = y2 , |
xn =, yn . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Определение 3. Вектор, все координаты которого равны нулю, называ- |
||||||||||||||||||||||||||
ется нулевым |
|
= (0, 0, |
, 0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Наиболее частыми операциями, которые совершаются |
|
|
над векторами, |
|||||||||||||||||||||||
является сложение и умножение на число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Определение 4. |
Пусть даны два n-мерных вектора |
|
|
= (x1, x,n ) и |
||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||
|
|
|
= (y1, y,n ). Суммой |
|
|
векторов |
|
+ |
|
называется |
|
|
вектор |
вида |
|||||||||||||||
|
y |
z |
|
x |
y |
|
|
||||||||||||||||||||||
|
|
= (x1 + y1, |
x2 + y2 |
, |
xn +, |
yn ) и записывают как |
|
= |
|
+ |
|
. |
|
|
|
|
|
|
|||||||||||
|
z |
z |
x |
y |
|
|
|
|
|
|
|||||||||||||||||||
Пусть λ – любое действительное число. Произведением вектора x на число λ называется n-мерный вектор c вида c = (λx1, λx2 , λxn,) и запи-
сывают как c = λ x .
Введенные выше две операции называют линейными операциями. Замечание. При геометрическом изображении векторов сумму 2-х векто-
ров можно находить по правилу параллелограмма
|
|
|
х |
у |
х |
х + у |
|
||
|
|
|
|
|
|
у |
|
|
|
|
|
х + у |
||
Позже убедимся, что такое определение приводит к тому же результату, что и ранее.
§ 2. Понятие n-мерного векторного пространства
Так как линейные операции (сложение и умножение на число) сводятся к операциям над их координатами, а они в свою очередь являются обычными действительными числами, то легко проверить справедливость следующих свойств введенных выше операций над векторами.
Пусть x, y, z – произвольные n-мерные векторы. Тогда:
1)x + y = y + x −переместительный закон (или коммутативность);
2)(x + y)+ z = x +(y + z)−сочетательный закон (или закон ассоциативности относительно сложения);
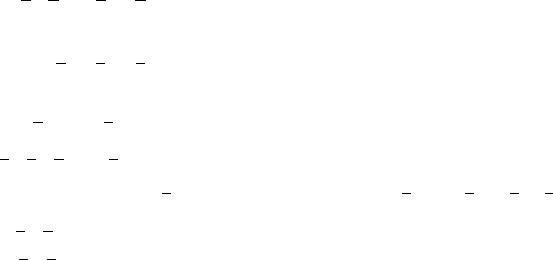
Лекция №1 |
Векторы и операции над ними |
проф. Дымков М.П. |
4 |
3) λ(x + y)= λx + λy , где λ – действительное число (дистрибутивный закон относительно сложения векторов);
4)(λ + µ)x = λx + µx , где λ, μ – действительные числа (дистрибутивный закон относительно сложения чисел);
5)λ(µx)= (λµ)x −ассоциативный закон относительно умножения на числа;
6)x + 0 = x , где 0 = (0, , 0) ;
7)для любого вектора x существует такой вектор (−x), что x +(−x)= 0;
8)1 x = x ;
9)0 x = 0.
Определение 5. Совокупность всех n-мерных векторов с линейными операциями (сложение и умножение на действительное число), подчиняющиеся свойствам 1) – 9), называется n-мерным линейным (или векторным) пространством. Если координаты векторов – действительные числа, то про-
странство называется арифметическим и обозначается Rn .
Например, R1 = R −множество действительных чисел – одномерное арифметическое пространство.
Отметим, что в определение векторного пространства не входит никакое умножение вектора на вектор.
Замечание. Множество всех векторов могут образовывать и другие алгебраические структуры , такие как группа, кольцо, тело, метрическое пространство и др. Эти структуры получаются, если при определении операций над векторами отказаться от некоторых привычных нам свойств или допустить другие операции (например, от свойства коммутативности, или ввести новую операцию умножения вектора на вектор и т.д.) .
Замечание. Линейные пространства могут быть образованы не только лишь с помощью векторов, эти пространства могут быть построены из объектов самой различной природы (возможность такого абстрагирования, а значит, и разработки универсальных методов исследования, отличает математику от других наук!). Например:
1) множество P[x] всех многочленов от одной действительной переменной с действительными коэффициентами, если сложение и умножение на число определить обычным образом;
2)множество всех бесконечных последовательностей чисел (x1,..., xn ,....), если сложение и умножение определить покомпанентно;
