©БГЭУ Лекция №11 Производная функции проф. Дымков М.П. 93

Геометрический смысл производной следует из определения и приведенных в п.1 пояснений о проведении касательной к графику функции. Отсюда сле-

дует, что угловой коэффициент касательной к графику функции в точке

M0 (x0 , f (x0 )) равен k = tgφ = f ′(x0 ). Следовательно, уравнение касательной в точке M0 (прямая с заданным угловым коэффициентом k, проходящая через заданную точку M0 ) есть

y = f ′(x0 )(x − x0 )+ f (x0 ).

Физический смысл для материальной точки с уравнением движения s = s(t) . Мгновенная скорость в момент t0 равна v(t0 )= s′(t0 ).

3. О связи дифференцируемости и непрерывности функций

При определении производной мы предполагали: 1) существование f (x) в точке x0 и ее окрестности;

2) существование предела lim ∆y . Как это связано с непрерывностью функции?

∆x→0 ∆x

Теорема. Если функция дифференцируема, то она непрерывна.

Замечание. а) Существуют функции, которые во всей области определения (т.е. везде) являются разрывными (например, функция Дирихле).

б) Существуют непрерывные функции, везде не имеющие производной. (примеры таких функций даны Вейерштрассом, Лагранжем (функции типа «зубьев пилы») и др.).

§ 2. Основные правила дифференцирования. Логарифмическая производная. Таблица производных основных элементарных функций

Изложим (Упр. –доказать) основные правила дифференцирования: арифметических выражений.

Пример. Вычислить производную функции y = (3x3 − 2x +1) sin x .

Функция представляет собой произведение двух функций, поэтому следует применить правило дифференцирования произведения, а затем правило дифференцирования суммы и табличные производные степенной функции и синуса:

=(3x3 − 2x +1)' sin x + (3x3 − 2x +1) (sin x)'=

=(9x2 − 2) sin x + (3x3 − 2x +1) cos x .

2)Дифференцирование сложных функций.

производную y′z = fz′(z0 ), то сложная функция y = f (φ(x)) имеет производную

4) Дифференцирование неявных функций.

Пусть есть неявная функция F(x, y) = 0 (т.е. ни одна из переменных явно не выражена через другую, например, – x2 + y2 −1 = 0 ). Очевидно, что можно

дифференцировать, выразив одну из переменных как функцию другой переменной. Однако дифференгцирование можно осуществить и без преобразования в явную функцию. Покажем на примере (подробнее во 2 семестре – в разделе о функциях 2-х переменных).

Пусть x2 + y2 − a2 = 0. Дифференцируем обе части равенства, учитывая правила дифференцирования сложной функции (y = y(x)):

вычислим ее производную (ln y)′ = yy′, которая называется логарифмической производной.

относительной скоростью изменением функции y = f (x) .

Это понятие используется в экономической литературе. Также оно полезно при вычислении сложных (степенно-показательных или содержащих много сомножителей).

Пример. y = xx ln y = xln x yy′ = ln x + xx y′ = y(ln x +1) = xx (ln x +1) .

7) Таблица производных простейших элементарных функций

Исходя из вышеизложенного, имеем следующую таблицу производных простейших функций:

1)(c)′ = 0, (c −const);

5)(sin x)′ = cos x .

6)(cos x)′ = −sin x ;

7)(tg x)′ = cos12 x ;

8)(ctg x)′ = −sin12 x ;

9)(arcsin x)′ = 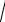1−1 x2 ;

10)(arccos x)′ = − 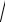1−1 x2 ;

11)(arctg x)′ =1+1x2 ;

12)(arcctg x)′ = −1+1x2 .

Приведенные выше формулы производных вместе с правилами дифференцирования суммы, разности, произведения, частного и правила дифференцирования сложной функции являются основными методами дифференцирования функции. С их помощью можно найти производную любой элементарной функции.