© БГЭУ Лекция № 13-14 Исследование функций с помощью производных проф. Дымков М. П. 119
Выпуклость функции. Точки перегиба
Определение. График функции y = f (x) , дифференцируемой на интервале (а; b), имеет на этом интервале выпуклость, направленную вверх (вниз), если
график этой функции в пределах интервала (а;b) лежит не выше (не ниже) любой своей касательной (рис. 7).
|
Теорема 5. (об условиях выпуклости вверх или вниз). |
|
y |
|
|
|
|||||||||||||
|
Пусть |
функция |
y = f (x) |
определена |
на |
интервале |
|
|
y = f ( x ) |
||||||||||
(a;b) и |
имеет |
непрерывную, |
не равную |
нулю в |
точке |
|
|
|
|
|
|||||||||
x0 (a;b) |
вторую производную. Тогда, если |
f (x) > 0 |
всюду |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
на интервале (a;b) , то функция имеет выпуклость вниз на |
|
|
a |
b |
х |
||||||||||||||
этом интервале, если |
f (x) < 0, то функция выпукла вверх. |
|
|
|
|||||||||||||||
|
|
Рис. 7 |
|
||||||||||||||||
|
|
|
|
|
|
′′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
y = f ( x ) |
|
|
|
|
◄Пусть в точке M (x0, f (x0 )) |
(рис. 8) прямая l |
||||||||||||
|
|
|
|
касается |
кривой |
y = f (x) . Обозначим |
через |
y |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
М |
|
|
|
|
переменную ординату |
точки |
прямой |
l. |
Тогда |
|||||||||
|
|
|
|
|
|||||||||||||||
|
l |
|
y |
|
y |
|
уравнение прямой l, касательной к кривой y = f (x) , |
||||||||||||
|
|
|
|
имеет вид: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x0 |
x |
|
|
х |
|
|
y = |
f (x0 ) + f ′(x0 ) (x − x0 ) . |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Рис. 8 |
|
|
|
Функцию |
y = f (x) |
разложим |
в |
ряд |
Тейлора |
в |
|||||||
окрестности точки x0 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
y = f (x) = f (x0 ) + |
f ′(x0 ) |
(x − x0 ) + |
f ′′(x0 ) |
(x − x0 )2 + o((x − x0 )2 ) |
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1! |
|
|
|
|
2! |
|
|
|
|
|
|
|
|
Возьмем произвольное значение х из окрестности точки x0 и найдем разность
y - y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y - y |
= f (x) − |
f (x ) |
+ |
f ′(x0 ) |
(x − x ) |
. |
|
||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
1! |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Заменим функцию |
y = f (x) |
рядом Тейлора. Получим: |
|
|
||||||||||||
|
|
f |
′ |
|
|
|
|
f |
′′ |
|
) |
|
|
|
|
|
|
(x ) |
|
|
|
(x |
|
|
|
||||||||
y - y = f (x0 ) + |
|
|
0 |
(x − x0 ) + |
|
|
|
0 |
|
(x − x0 )2 + o((x − x0 )2 ) |
- |
|||||
|
1! |
|
|
2! |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
−f (x0 ) + f ′(x0 ) (x − x0 )
1!
После раскрытия скобок будем иметь
y- y = f ′′2!(x0 ) (x − x0 )2 + o((x − x0 )2 ).
Вполученном выражении первое слагаемое в правой части определяет величину
© БГЭУ Лекция № 13-14 |
Исследование функций с помощью производных |
проф. Дымков М. П. 120 |
и знак разности y - y , второе слагаемое является бесконечно малой величиной. |
||
Из равенства следует, что знак разности y - y совпадает со знаком f ′′(x0 ) . |
||
Поэтому, если |
f ′′(x0 ) > 0, то y - y > 0 для всех точек |
x ≠ x0 , достаточно |
близких к точке x0 . Точки кривой расположены выше своей касательной и, в соответствии с определением, кривая выпукла вниз. Если f ′′(x0 ) < 0 , то y - y < 0 . Точки кривой расположены ниже своей касательной и кривая выпукла
вверх.► |
|
|
|
|
|
|
|
|
|
|
|||
Определение. Точкой |
перегиба графика функции |
y |
||||
y = f (x) называется |
точка |
M (x1, f (x1)), разделяющая |
||||
y = f (x) |
||||||
промежутки выпуклости вверх и вниз. Иными словами, |
M (x1, f (x1)) |
|||||
точка M (x1, f (x1)) - точка перегиба кривой, если в этой |
|
|
||||
точке кривая переходит с одной стороны касательной на |
|
х |
||||
другую, меняя направление выпуклости (рис. 9). |
|
|||||
x1 |
||||||
|
|
|
|
Рис. .9 |
||
|
|
|
||||
Теорема 6. (о необходимом условии точки перегиба). |
|
|
||||
Если M (x1, f (x1)) |
есть точка перегиба дважды дифференцируемой |
|||||
функции y = f (x), то f ′′(x1) = 0 или f ′′(x1) = ∞. |
|
|
||||
Теорема 7. (о достаточном условии точки перегиба). |
|
|
||||
Если вторая производная f (x) |
дважды дифференцируемой функции при |
|||||
|
|
′′ |
|
|
|
|
переходе через некоторую точку x1 |
меняет знак, причем |
f ′′(x1) = 0, то точка |
||||
M (x1, f (x1)) есть точка перегиба кривой y = f (x).
Схема исследования функции на выпуклость
1)Найти вторую производную функции;
2)найти точки, в которых вторая производная равна нулю или обращается
вбесконечность;
3)исследовать знак производной слева и справа от каждой найденной точки и сделать вывод об интервалах выпуклости и точках перегиба;
4)найти значения функции в точках перегиба.
Пример 11. Найти интервалы выпуклости и точки перегиба функции y = x3 −3x2 + x −1.
Находим вторую производную:
y′ = 3x |
|
−6x +1, y′′ = 6x −6 . |
′′ |
- |
+ |
2 |
f (x) |
||||
|
|
|
|
|
|
Находим точку, где вторая производная равна |
|
∩ 1 |
х |
||
|
|
||||
нулю: y′′ = 0 при х=1. |
|
Рис. 10 |
|
||
© БГЭУ Лекция № 13-14 |
Исследование функций с помощью производных проф. Дымков М. П. 121 |
Исследуем знак второй производной слева и справа от найденной точки. Для этого рисуем числовую ось и указываем на ней знаки второй производной (рис.10). Делаем заключение об интервале выпуклости вверх слева от точки х=1 и интервале выпуклости вниз справа от этой точки.
Делаем вывод о наличии перегиба в точке (1;2).
Асимптоты графика функции
Прямая x = x0 называется вертикальной асимптотой графика функции
y = f (x) , |
если хотя бы одно из предельных значений |
lim f (x) |
или |
|
|
|
x→x0 −0 |
|
|
lim f (x) равно +∞ или −∞. |
|
|
|
|
x→x0 +0 |
|
|
|
|
Прямая y = y0 называется горизонтальной асимптотой |
графика |
функции |
||
y = f (x) , |
если хотя бы одно из предельных значений lim f (x) или |
lim |
f (x) |
|
|
x→+∞ |
|
x→−∞ |
|
равно b.
График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая y = kx +b называется наклонной |
|
|
у |
|
|
|
||
|
|
|
|
|
||||
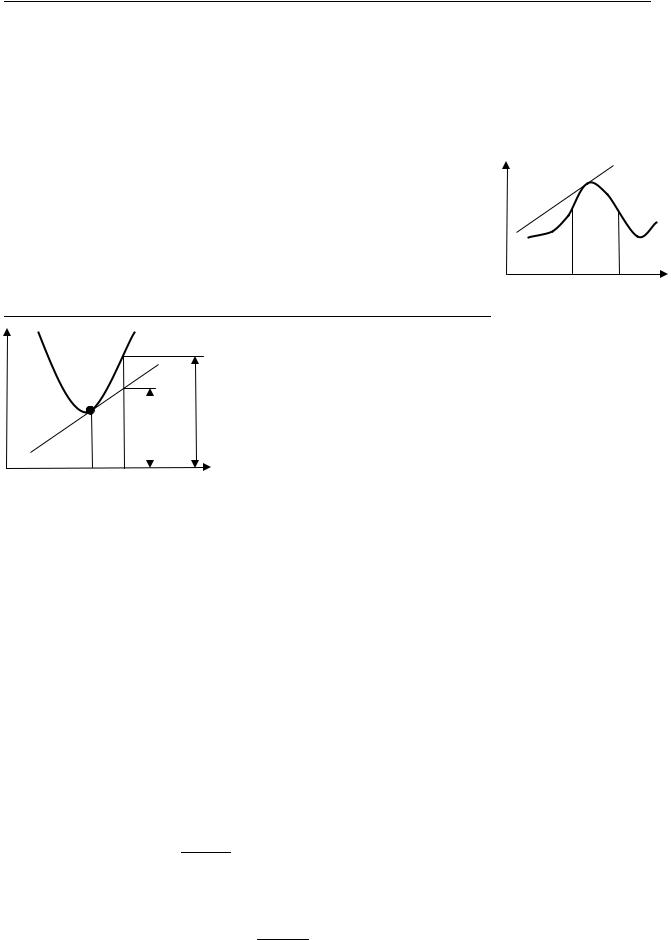
асимптотой графика функции y = f (x) , если |
|
|
y = f ( x ) |
|
|
|
||
|
|
|
|
|
|
|
|
|
lim ( f (x) − kx −b)= 0, |
|
|
|
|
y = kx +b |
|||
x→∞ |
|
|
|
|
|
х |
||
т.е. когда функция при x → ∞ представима в виде |
|
|
||||||
|
Рис. 11 |
|
|
|
||||
f (x) = kx +b +α(x), где lim α(x) = 0. |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
x→+∞ |
|
|
|
|
|
|
|
Существование |
асимптоты y = kx +b у |
кривой y = f (x) при x → ∞ |
||||||
означает, что при |
x → ∞ функция |
ведет себя «почти как линейная», |
т. е. |
|||||
отличается от линейной функции |
y = kx +b |
|
бесконечно мало (рис. |
11). |
|
|
||
Наклонная асимптота может быть как правой, так и левой.
Теорема 8. (об условиях существования наклонной асимптоты)
Если для функции y = f (x) существуют пределы
lim |
f (x) |
= k и |
lim ( f (x) − kx)= b , |
|
|
|
|
|
|
||||
x→∞ |
x |
x→∞ |
|
|
||
то функция имеет наклонную асимптоту y = kx +b при x → ∞. |
||||||
◄Из существования первого предела следует, что |
f (x) |
− k = β(x) , где |
||||
x |
||||||
|
|
|
|
|
||
β(x) - бесконечно малая функция. Тогда f (x) = kx + x β(x). Отнимем от обеих
© БГЭУ Лекция № 13-14 |
Исследование функций с помощью производных |
проф. Дымков М. П. 122 |
|
частей величину kx и найдем предел при x → ∞, lim ( f |
(x) − kx)= lim x β(x) . |
||
Из lim ( f (x) − kx)= b |
x→∞ |
|
x→∞ |
следует lim x β(x) = b . Поэтому |
|
x β(x) = b +α(x) , где |
|
x→∞ |
x→∞ |
|
|
α(x) - бесконечно малая функция.
Следовательно, f (x) = kx + x β(x) = kx +b +α(x) .►
Пример 12. Найти асимптоты графика функции y = 
x(x - 2) .
Решение. Найдем последовательно пределы lim f (x) и lim ( f (x) − kx).
x→∞ x x→∞
Второй предел находится при условии, что первый из них конечен.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f (x) |
|
|
|
|
|
|
|
|
− x |
. |
||||
Тогда lim |
= lim |
|
x(x - 2) |
|
= lim |
|
|||||||||
|
|
|
|
|
|
|
|||||||||
x |
|
x |
|
|
|
|
|
|
x |
|
|||||
x→∞ |
x→∞ |
|
x→∞ |
|
|
|
|
|
|
|
|||||
Если x > 0, то модуль раскрываем со знаком плюс, и получаем
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1− x |
|
|
|
|
|
|
|
|
=1. |
|
|
|
|
|||||
k = lim |
|
= |
|
lim |
1 |
− 2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
x→+∞ |
|
|
x |
|
|
x→+∞ |
|
|
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
−x |
|
1− 2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
Если x < 0 , то |
k = |
|
|
|
|
|
|
x |
|
|
|
|
|
|
= −1. |
||||
lim |
|
|
|
|
|
= |
lim |
− |
1− |
|
|||||||||
|
|
|
x |
|
x |
||||||||||||||
|
|
|
x→−∞ |
|
|
|
|
|
x→−∞ |
|
|
|
|
||||||
Найдем величину второго предела, домножив числитель и знаменатель (который равен единице) на сопряженное выражение:
lim ( f (x) − kx)= |
lim |
( |
|
|
− x)= |
lim |
x(x − 2) − x2 |
= |
|||||||||||
x(x − 2) |
|||||||||||||||||||
|
|
|
|||||||||||||||||
|
x(x − 2) + x |
||||||||||||||||||
x→+∞ |
|
|
|
x→+∞ |
|
|
|
|
|
|
|
|
x→+∞ |
|
|
||||
= lim |
|
−2x |
|
= |
lim |
|
|
−2 |
|
= −1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x→+∞ |
x |
1− 2 +1 |
|
x→+∞ |
1 |
− 2 |
+1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||
Таким образом, правая наклонная асимптота имеет вид y = x -1.
Аналогично рассматривается случай x → -∞. |
|
||||||||||||||||
lim |
( f (x) − kx)= |
lim |
( |
|
|
+ x)= lim |
x(x − 2) − x2 |
= |
|||||||||
x(x − 2) |
|||||||||||||||||
|
|
|
|||||||||||||||
x→−∞ |
|
|
|
x→−∞ |
|
|
|
|
|
|
x→−∞ |
|
x(x − 2) − x |
|
|||
lim |
|
−2x |
|
= |
lim |
2 |
|
|
=1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x→+∞ |
|
|
x→+∞ |
1− 2 |
+1 |
|
|
|
|
||||||||
|
−x |
1− 2 +1 |
|
|
|
|
|
|
|
||||||||
|
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|||
Тогда получим левую наклонную асимптоту y = -x +1. График исходной функции со своими асимптотами представлен на рис. 12.