3) множество C[a,b] всех непрерывных на отрезке функций с поточечным заданием операций.

§ 3. Скалярное произведение векторов

Понятие n-мерного пространства Rn , при n > 3 далеко не в полной мере обобщает привычные пространства R2, R3 . Так, например, пока не определены понятия длины вектора, угла между векторами (например, как это представить

в 5-мерном пространстве R5 ). Оказывается, что положение можно исправить путем введения понятия скалярного произведения векторов.

Определение. Скалярным произведением (x, y) двух векторов x = (x1, x,n ) и y = (y1, y,n ) называется число, равное сумме произведений соответствующих (одноименных) координат

n

(x, y) = x1 y1 + x2 y2 + + xn yn = ∑xi yi .

i=1

Из данного определения следуют следующие основные свойства скалярного произведения векторов:

1)(x, y)= (y, x);

2)(λx, y)= λ(x, y);

3)(x + y, z)= (x, y)+(y, z);

4) (x, x)≥ 0 при x ≠ 0 и (x, x)= 0 x = 0 .

Для доказательства какого-либо из свойств 1) – 4) достаточно, например, найти числа в левой и правой частях соответствующих выражений и убедиться, что они равны. (Упр.)

Определение. Векторное пространство с введенным в нем скалярным произведением называется евклидовым пространством.

Определение. Длиной n-мерного вектора x называется число 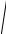(x, x) (арифметическое значение квадратного корня). Длину вектора будем обозначать x или x , (чтобы не смешивать с понятием абсолютных величин).

Таким образом, длина любого вектора есть x = 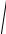(x, x) или x = (x, x) .

Из свойства 4) следует, что каждый n-мерный вектор x обладает длиной, причем нулевой вектор 0 является единственным вектором, длина которого равна 0.

Иногда скалярное произведение (x, x) называют скалярным квадратом

вектора x и обозначают x2 . Тогда из формулы длины вектора следует x 2 = (x, x)= x2 , т.е. квадрат длины вектора равен скалярному квадрату. Можно доказать, что верно следующее утверждение.

Теорема. Если x и y − n-мерные векторы, то справедливы соотношения:

1)λx = λ x , где λ – число;

2)(x, y) ≤ x y −(неравенство Коши-Буняковского;

3)x + y ≤ x + y − (неравенство треугольника).

что и требовалось доказать.

§ 4. Угол между n-мерными векторами

Из неравенства Коши-Буняковского (x, y) ≤ x y следует двойное неравенство

которое принадлежит отрезку [0, π].

Таким образом, скалярное произведение равно произведению длин этих векторов на косинус угла между ними.

Замечание. Часто в качестве определения скалярного произведения векторов принимают равенство (3). В этом случае требуются некоторые пояснения понятия угла между векторами в n - мерном пространстве.

Определение. 1) Два ненулевых n-мерных вектора x и y называются

коллинеарными, если угол между ними равен 0 или π. Если φ = 0, то векторы называют одинаково направленными, если φ =π , то противоположно направ-

вами, векторы коллинеарны, когда одноименные координаты векторов пропорциональны (с одним и тем же коэффициентом пропорциональности λ! ), т. е.

x1 =... = xn = λ . y1 yn

Замечание. При геометрическом изложении векторов, определение коллинеарных векторов звучит так: говорят, что векторы на плоскости (и в пр о- странстве) коллинеарны, если они лежат на одной прямой или на параллельных прямых. Далее, три вектора в пространстве называют компланарными, если эти векторы лежат в одной плоскости или в параллельных плоскостях.

Замечание. (Упр.* ). Существуют, помимо скалярного произведения векторов, другие понятия произведения векторов. Например:

1) векторное произведение 2-х векторов x × y , результатом которого яв-

ляется не число, а вектор; 2) смешанное (векторно-скалярное) произведение 3-х векторов

( x × y , z), результатом которого является число.

Имеется определенный геометрический и физический смысл таких произведений. Например, векторное произведение используется для проверки коллинеарности векторов, вычислении площадей параллелограмма и треугольника, для нахождения линейной скорости вращения твердого тела). Смешанное произведение можно использовать для определения компланарности векторов, вычисления объема параллепипеда, пирамиды и др.

§ 5. Линейная зависимость векторов

При решении различных задач, как правило, приходится иметь дело не с одним вектором, а с некоторой совокупностью векторов обычно одинаковой размерности, которую обозначим как

k

b = ∑λi ai .

i=1

Замечание. Вспомним, что два вектора b и a называются коллинеарны-

ми, если b = λa , где λ – некоторое число. Поэтому в некотором смысле понятие линейной комбинации векторов обобщает понятие коллинеарных векторов. Здесь мы объединили две операции – сложение векторов и умножение векторов на число.

Пример. a1 = (1, 2, 0) , a2 = (2, 1, 1) , a3 = (−1, 1, − 2). Пусть λ1 = 2 , λ2 = 3,

λ3 = 4 . Тогда линейная комбинация векторов есть b = λ1a1 + λ2 a2 + λ3 a3 =