Лекция №10

Предел функции. Непрерывность функций

проф. Дымков М.П. 80

Односторонние пределы

Определение. Число А называется правым пределом функции

f (x) в

точке

x ,

если

для

{x },

x → x ,

x > x ,

соответствующая

0

n

n n→∞

0

n

0

последовательность значений

{ f (xn )} → A .

При

этом, правый

предел

A = f (x0 + 0)= lim

n→∞

обозначают

f (x) =

lim

f (x) . Аналогично, определяется

x→x0

+0

x→x0 ,x>x0

левый предел

A = f (x0

−0)=

lim f (x).

x→x0 −0

Связь между односторонними пределами и пределом функции в точке

устанавливается следующим утверждением:

Теорема. Функция

f (x) имеет предел в точке x0

тогда и только тогда,

A = lim f (x) =

lim

f (x) = lim f (x).

x→x0

x→x0 +0

x→x0 −0

f (x) =

x

X = R \ {0} x0 = 0

+1

x

lim

x

= lim

x

=1

lim

x

= lim

− x

= −1

–1

x→0+ x

x→0+ x

x→0− x

x→0−

x

f (x0 −0)≠ f (x0 + 0)

lim f (x) – нет предела в точке x0 = 0.

x→x0

которые представля N ют

собой пределы функций, определенных на

специальном множестве –

множестве

натуральных чисел так что члены

последовательности есть

an = f (n) .

Нетрудно видеть, что эти свойства

Теорема. Если

функции f (х)

и

g(х)

имеют в точке x = x0 предел

A = lim f (x) ,

B = lim g(x), то:

x→x0

x→x0

1)

lim ( f (x) ± g(x)) = lim

f (x) ± lim g(x) = A ± B ;

x→x0

x→x0

x→x0

2)

lim (c f (x)) = c lim

f (x) = c A ;

x→x0

x→x0

3)

lim ( f (x) g(x)) = lim

f (x) lim g(x) = A B ;

x→x0

x→x0

x→x0

f (x)

lim f (x)

A

4)

lim

=

x→x0

=

, если B ≠ 0 .

g(x)

lim g(x)B

B

x→x0

x→x0

Пример. lim

2x2

−3x + 6

=

2

4 −3

2 +

6

=

8

=

2

.

x2

+3x + 2

4 +

3 2

+ 2

12

3

x→2

Например.

y = x cos 1 ,

x

= 0 .Т.к. у = х – б.м. в т. x = 0, а

y =

cos 1

≤1,

x

0

0

x

то

lim x cos

1 = 0

(как произведение б.м. на ограниченную функцию).

x→∞

x

Если

значения функции f

(х)

стремятся

к бесконечности при x → x0

, то можно ввести следующее понятие (бесконечного) предела.

f (x) → ∞

x→x0

Будем

говорить, что

lim

f (x) = ∞

(+∞ или −∞) ,

если

для

x→x0

M > 0

δ > 0 что для всех

x − x0

<δ выполнено условие

f (x)

> M .

где α(x),

β(x) −

б.м.ф.

в

точке

x = x0 . В

этом

случае

такое выражение

символически записывают

как

0

и

называют неопределенностью вида 0 .

0

0

Аналогично,

если

α(x)

и β(x) −

б.б.ф.

в

точке

x , то

выражение

α(x)

0

β(x)

называют неопределенностью вида

∞ .

∞

Примеры.

1)

x2 −5x

+ 6

0

(x − 2)(x

−3)

x −3

2 −3

= −1.

lim

=

= lim

= lim

=

+ 2

(x −

2)(x

−1)

x −1

2 −1

x→2 x2 −3x

0

5x + 2

∞

x(5 + 2)

5

+ 0

5

2)

x

.

lim

=

= lim

=

=

1

7

+ 0

7

x→∞ 7x +1

∞

x→∞

x(7

+ x)

x

5

2

+

3

+

7

2x2

−3x + 7

0

x4

x4

3)

lim

= lim

x3

=

=

0.

x5 (1+)

1

x→∞ x5 −3x3 +9

Подобным образом возникают

неопределенности других типов:

∞ −∞,

Лекция №10

Предел функции. Непрерывность функций

проф. Дымков М.П.

83

§ 2. Замечательные пределы. Сравнение функций. Символы O и o

Первый замечательный предел.

lim sin x

=1.

x→0

x

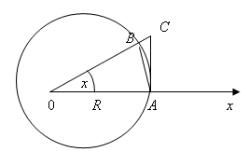
Рассмотрим круг радиуса R и

сделаем

дополнительные построения (см. рисунок).

Доказательство. Из рисунка следует

неравенство

S∆AOB < ScektopAOB < S∆OAC

или, используя равенство h = Rsin x

и

формулы для площадей сектора и треугольников ∆ , имеем

1 R2 sin x <

1 R2 x < 1 R2 tg x

или после сокращения

2

2

2

x

1

sin x

1<

<

или 1 >

> cos x .

sin x

cos x

x

Теперь в последнем неравенстве перейдем к пределу при x → 0

limcos x < lim sin x

< lim1 1< lim sin x

<1.

x→0

x→0

x

x→0

x

Факт

limcos x =1−установим позже в разделе непрерывность функций.

x→0

Примеры.

1) lim sin5x

= lim sin5x

5 =1

5 =

5 .

x→0

3x

x→0

5x

3

3 3

1−cos x

2sin

2 x

5

sin

x

sin

x

1

1

1

2) lim

= lim

2

= lim

2

2

= 2

1 1

=

.

x2

x2

3

x

x

4

4

2

x→0

2

2

3) lim tg x = lim sin x

1

=1 1 =1.

cos x

x→0

x

x→0

x

Второй замечательный предел.

+

1

x

lim 1

x

= e .

x→∞

Его доказательство

сводится

к

использованию

уже

известного предела

1 n

→ e .( Упр. )

числовой последовательности 1+

n

x→∞