Лекция № 15 |
Комплексные числа |
проф. Дымков М. П. 135 |
|
|
|
|
|
Раз появились новые числа, то неизбежно и рассмотрение функций от этих чисел. Переход к функциям от комплексной переменной дал возможность глубже изучить элементарные функции и установить интересные связи между ними. Например,
1)sin z >1 (вопреки школьным представлениям);
2)тригонометрические функции являются комбинациями показатель-
ных
cos x = 12 (ex
−1 + e−x
−1 );
3) функция ex −периодична (ее период равен 2π i ).
Вскрываются неожиданные соотношения между «знаменитыми» числами:
(eπ )i = −1 |
или (eπ ) |
−1 |
= −1 |
(коллекция трех удивительных чисел – |
||||
вполне порядочное число); |
|
|
|
|
||||
|
|
|
|
|
π |
|
|
|
Или еще ( |
|
) −1 = e− |
+2kπ , |
k = 0, ±1,... |
||||
|
2 |
|||||||
−1 |
||||||||
Вышесказанное становится любопытным и делает притягательным изучение комплексные числа.
2. Определение комплексных чисел
Чтобы уйти от упоминания о «сомнительном» символе i = 
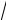−1 и всякой мистики, мы для построения множества комплексных чисел воспользуемся хорошо известными чисто алгебраическими операциями (как это делал Гамильтон), которые будем осуществлять над парой обычных действительных чисел и тем самым дадим вполне реальную (не мистическую) интерпретацию комплексным числам. Эту пару можно обозначать либо (а, b) либо
a |
. Нагляднее, как нам представляется, выбрать как |
a |
, где |
а, b R - |
||
|
|
|
|
|||
b |
|
b |
|
|
||
действительные числа.
Определение 1. Комплексными числами называются упорядоченные пары вещественных (действительных) чисел (или компонент), которые удовлетворяют следующим аксиомам:
|
|
|
|
|
a |
и |
c |
|
считаются равными, когда равны их компоненты, |
|
10. Пары |
|
|
||||||
|
|
|
|
|
b |
|
d |
|
|
|
a |
c |
a = c |
|
|
||||
т.е. |
b |
|
= d |
b = d ; |
|
|
|||
|
|
|
|
|
|
|
|
|
|
Лекция № 15 Комплексные числа проф. Дымков М. П. 137
Таким образом, аксиома 40 хорошо согласована с 10 – 30 и не приводит к путанице, т.е в се привычные свойства для действительных чисел сохраняются для этих чисел, записанных как комплексные числа.
Обратим внимание, |
|
что умножение на действительное число m R |
|||||||
a |
m a |
ma −0 b |
ma |
|
|
||||
есть m = |
|
= |
|
= |
, что соответствует умножению |
||||
b |
0 |
b |
mb + 0 a |
mb |
|
|
|||
компонент комплексного числа. Если |
m – натуральное, то с учетом преды- |
||||||||
дущего |
|
|
|
|
|
|
|
|
|
a |
ma |
a |
|
a |
a +... + a |
ma |
|||
m |
= |
|
= |
|
+... + = |
|
|
= |
, что согласуется с |
b |
mb |
b |
|
b |
b + |
... +b |
mb |
||
обычным последовательным сложением чисел.
В) Теперь надо еще проверить, что аксиомы 20 и 30 согласованы в себе и друг с другом так, что привычные нам действия над действительными числами сохраняются при переходе к комплексным числам.
Окаких «привычных» действиях идет речь?
1)Коммутативность сложения
a |
c |
a + c |
|
c + a |
|
c |
|
a |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
+ |
|
= |
|
|
|
= |
|
= |
|
+ |
. |
|
|
|
|
|
|
|
|
|
|
|
|||
b |
d |
b + d |
|
d +b |
d |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
2) |
Ассоциативность сложения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
a |
|
c |
|
e |
|
a |
|
c |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
+ |
|
+ |
|
= |
+ |
|
+ |
f |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
b |
|
d |
|
|
f |
|
b |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) |
Существование нулевого элемента |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
a |
|
0 |
a + 0 |
a |
|
Таким |
образом, |
|
пара |
|
0 |
40 |
есть |
«ноль» для |
|||||||||||||
|
|
+ |
|
= |
|
|
= |
|
|
|
=0 |
||||||||||||||||
b |
|
0 |
b + 0 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||
|
|
комплексных чисел. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4) |
Существование для каждой пары «противоположного» числа: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
+ |
|
−a |
0 |
|
= 0 . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
−b |
|
= |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
5) |
Коммутативность умножения (упр.). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
6) |
Дистрибутивные законы |
|
|
a |
|
c |
|
|
e |
|
= |
a e |
c e |
||||||||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
d |
|
|
f |
|
b |
f |
d |
f |
|||
