Загальна оцінка експериментальних засобів.

Достоїнства: простота описання доступність одержання моделей можливість побудови моделі за відсутності теорії процесу.

Недоліки :неможливість застосування моделі для режимів, для яких не

проводилися вимірювання; неможливість застосування моделі при переході до

інших установок; неможливість екстраполяцiї результатів.

Приклад

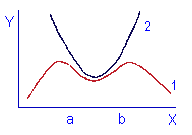
Модель будувалася для значень iнтервалу (а в)

Одержана квадратична залежність 2. Видно, що на iнтервалі (а в) модель добре описує процес, протікаючий в оригіналі, експериментальна залежність Y=f(X) відображається кривою 1. При виході величини значення X за межі відрізку (а в) модель (крива 2) дає чималі похибки.

Емпiричнi засоби корисні і застосуються для вивчення складних систем,

якщо їх структура не змінюється в часу, теорія процесу невідома і (або ) коли

необхідно хутко одержати модель без дослідження процесу.

1.5.2. Експериментально - аналітичний засіб

При використанні цього засобу дослідник намагається визначити фізичну суттєвість явищ, протікаючих в об'єкті. Використовується декомпозиція складного явища, т. є. на основі аналізу визначаються більш прості, елементарні процеси, що можна досліджувати більш доступними способами. Після аналізу впливу елементарних процесів на процес в цілому, несуттєві фактори відкидаються, і вибирається отой елементарний процес, що виявляє найбільш істотний вплив.

Після цього складається математичний опис, причому не в формі полiнома, а у вигляді залежності, що характерна для наданого елементарного процесу. Вплив інших елементарних процесів враховується зміною коефіцієнтів, входивших в цю залежність.

У вигляді прикладу розглянемо побудову моделі для опису процесу переносу

тепла в непорушному зернистомушарі в аксiальному напрямі .

Процес переносу тепла здійснюється за рахунок наступних процесів :

1 – конвекція

2 – теплопровідність

3 – випромінювання

При температурах менш 800 К та малих лінійних швидкостях потоку газу перенос тепла, в основному, визначається теплопровідністю.

Цей процес описується порівнянням Фур'є :

q = – λ * dt/dх (1. 4 )

де λ - дійсне значення теплопровідністю.

Однак користуватися порівнянням (1.4) ще не можна, так як. в ньому не враховані 1 та 3 елементарні що складають процес переносу тепла. Для їх обліку замість дійсного значення λ вводиться деяке " ефективне " значенняλ_еф, що визначається експериментально, тоді порівняння (1. 4 ) приймає вид:

q = – λ _еф* dt/dx (1. 5)

Рівняння (1.5) є експериментально-аналітичною моделлю процесу переносу тепла в непорушному зернистому шарі. Цілком очевидно, що λ_ефне є фізичною константою, а залежить від умов експериментів, при яких вона була одержана від масштабів установки.

Достоїнства: - краще описує нелінійні властивості об'єкту моделювання,

так як дозволяє більш надійно вибирати вигляд порівняння.

Недоліки : - ефективні коефіцієнти змінюються у залежності від умови проведення опитів, тому експериментально – аналітична модель справедлива лише в тому iнтервалі, у якому вироблявся експеримент.

Зіставимо емпiричний та експериментально–аналітичний засоби

побудови математичних моделей. Експериментально–аналітичний засіб має перевагу перед чисто експериментальним в тому, що він відбиває теорію процесу.

Для обліку впливу явищ, не обчислених при складанні моделі, вводяться ефективні коефіцієнти. В першому засобі експеримент необхідний для одержання моделі, в другому - для визначення коефіцієнтів моделі.