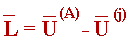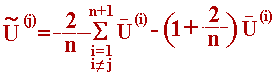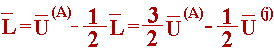5. 7. 7. Симплексний метод

Основна ідея цього методу укладається в тому, що по відомим значенням цільової функції у вершинах опуклого многогранника, що називається симплексом, знаходиться напрямок, у якому вимагається зробити наступний крок, щоб одержати найбільше зменшення (збільшення) значення цільової функції. При цьому під симплексом в n-мірним просторі розуміється многогранник, що має n+1 вершину. Прикладом симплекса в двомірним просторі, т. є. на площині, є трикутник. В трьохмірним просторі - тетраедр. Симплекс володіє наступною властивістю - проти будь-який з його вершин Sj розміщена тільки одна грань, на якої можна збудувати новий симплекс, що відрізняється від колишнього розміщенням нової вершини Sj тоді як інші вершини обох симплексів співпадають. Вершина нового симплекса S, взагалі кажучи, може знаходитися і по іншу сторону грані від вершини Sj.

Ця властивість симплекса і обумовлювала можливість його застосування при рішенні задач оптимiзації.

Розглянемо найпростіший випадок - пошук мінімуму цільової функції двох перемінних R(U₁ ,U₂ ).

Алгоритм пошуку наступний:

1. Розраховуються значення цільової функції у вершинах обраного вами симплексаS₁₀, S₂₀, S₃₀ (рис.5.27).

2.Вибирається вершина, де значенняR(U₁ ,U₂)найбільше -S₁₀.

3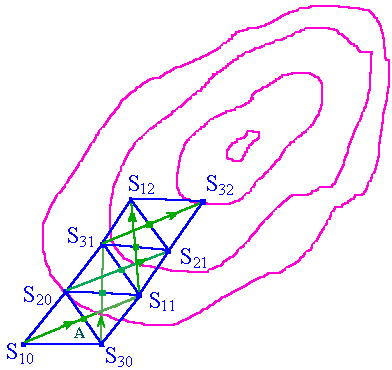.Новий симплексS₁₁ ,S₂₀ ,S₃₀ будується таким засібом: - знаходиться середина граніS₂₀ ,S₃₀ , яка розташована проти вершиниS₁₀ - крапка А. Через крапкиS₁₀іАпроводиться пряма. На цій прямій від крапкиАвідкладається відрізокАS₁₁, рівний по величині відрізку S₁₀ А.

4.У новій вершині обчислюється значення цільової функції.

5. З вершин нового симплексаS₁₁, S₂₀, S₃₀вибирається та, де значення цільової функції максимально.Рис.5.27

6.Аналогічноп.3будується новий симплексS₁₁, S₂₀, S₃₁, тобто

виключається вершина S₃₀, що мала найбільше значення цільової функції і т.д.

У результаті застосування розглянутої процедури виключення вершин симплексів з найбільшим значенням цільової функції процес пошуку сходиться до мінімального значення R(U₁ ,U₂ ). При виникненні зациклення в околицях крапки екстремуму необхідно зменшувати розміри симплекса.

Критерієм закінчення пошуку можуть служити розміри симплекса. Наприклад, якщо всі ребра симплекса стануть менше δ, те пошук можна припиняти.

Розглянемо алгоритм симплексного методу для задач довільної розмірності.

Нехай вершинам вихідного симплекса S_i (i=1,2,...,n+1)відповідають координати

U⁽ⁱ⁾=(U⁽ⁱ⁾₁ ,U⁽ⁱ⁾₂ ,..., U⁽ⁱ⁾_n), (i=1,2,...,n+1). І нехай найбільше значення цільової функції відповідає вершиніS_j. Визначимо координати вершиниŜ_jнового симплекса.

Вершина Ŝ_jрозташовується симетрично вершиніS_j щодо середини грані, що знаходиться проти вершиниS_j. Координати центра цієї граніU⁽ⁱ⁾визначаються по формулі: (5.62) причому підсумовування ведеться тільки по тим векторамU⁽ⁱ⁾, що відповідають вершинамS_i, що утворюють цю грань. Вектор, що характеризує відстань від вершиниS_jдо центра грані, яка розташована проти цієї вершини, буде:

(5.63)

Координати вершини S_jвизначаються по формулі

(5.64)

Підставивши в (5.64) вираження для Uз (5.62), одержимо:

(5.65)

Формула (5.65)визначає координати вершиниS_jнового симплекса.

При необхідності зменшити розміри симплекса (у випадку зациклення в околиці крапки оптимуму) замість формули (5.63)можна користатися наступним вираженням:

(5.66)

Найбільше ефективно симплексний метод сходиться при використанні правильних симплексів - рівностороннього чи трикутника тетраедра, утвореного рівносторонніми трикутниками. У цьому випадку напрямок пошуку збігається з напрямком градієнта (якщо симплекс досить малий).

Симплексний метод володіє ще одним важливим достоїнством- при збільшенні розмірності задачі обчислювальні витрати зростають незначно, тому що на кожнім кроці вважається тільки одне значення цільової функції.