
Корольов / Теория связи
.pdf
4.4.2. Количество информации, переданной по непрерывному каналу
Рассмотрим непрерывный источник с дискретным временем, в котором амплитуды импульсов статистически независимы друг от друга. Предположим, что в канале действует аддитивная помеха n(t) с широким спектром, не завися-
щая от очередных и предыдущих импульсов. Тогда на выходе получим последовательность импульсов с амплитудами y(t1 ), y(t2 ),..., y(tk ), статистически не за-
висящими друг от друга.
|
Свойства источника непрерывного сигнала будут определяться ПРВ w(xi ), |
||||||||||||||
i =1,2,..., k |
входных (информационных) случайных величин |
x(ti ), а воздействие |
|||||||||||||
помехи будет определяться условными ПРВ |
|
|
|
|
|
|
|
|
|
|
|||||
w yi x |
|
выходных |
СВ |
y(ti ) при заданных |
xi + ∆x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
i |
|
|
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
входных СВ x(ti ) (рис. 4.5). |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
x1 |
|
|
|
|
|
|
|
|
|||||||
|
Разделим области определения вели- |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∆t |
2∆t 3∆t |
|
||||||||
чин |
x и y на малые отрезки длиной ∆x и |
|
|
|
|
|
|
|
|
|
|
||||
∆y . |
Вероятность |
p(xi ≤ x < xi + ∆x) того, что |
|
|
|
|
|
|
|
|
|
|
|||
значение x лежит на некотором отрезке xi ≤ x < xi |
+ ∆x , приблизительно рав- |
||||||||||||||
на |
w(xi )∆x . Аналогично, |
p(y j ≤ y < y j +∆y)≈ w(y j |
)∆y , |
|
а совместная вероятность |
||||||||||
этих двух событий будет w(xi , y j )∆x∆y . При такой дискретизации количество информации, переданное по каналу и рассчитанное на один импульс, приближенно находится по формуле:
I (Y , X )∆∆yx = ∑∑w(xi , y j )∆x∆y log |
w(xi , y j |
)∆x∆y |
. |
|
w(xi )∆xw(y j )∆y |
||||
i j |
|
|||
Устремив ∆x и ∆y к нулю, перейдем к непрерывному каналу. При этом двойная сумма преобразуется в двойной интеграл, а количество передаваемой информации
I (Y , X )= lim I (Y , X )∆∆x |
= |
+∞+∞w(x, y)log |
w(x, y) |
dxdy . |
(4.10) |
|
|
||||||
∆x→0 |
y |
|
∫ ∫ |
w(x)w(y) |
|
|
∆y→0 |
|
|
−∞−∞ |
|
|
|
161

Отметим следующие свойства количества информации, передаваемой в непрерывном канале:
I (Y , X )≥ 0 , причем I (Y , X )= 0 тогда и только тогда, когда вход и выход ка-
нала статистически независимы, т.е. w y x = w(y);
I (Y , X )= I (X ,Y ) – свойство симметрии;
I (Y , X )= ∞, если помехи в канале отсутствуют, т.е. y = x , n = 0 .
Можно показать, что энтропия источника неограниченно возрастает, когда его алфавит переходит от дискретного к непрерывному. Для этого разделим область определения непрерывного сигнала x на отрезки ∆x (рис. 4.5), и превратим сигнал в дискретный, положив вероятность появления xi , равной w(xi )∆x . Энтропия такого дискретного сигнала
H ∆x (X )= ∑i w(xi )∆x log w(x1i )∆x .
Устремим теперь ∆x к нулю для перехода к энтропии непрерывного сигнала [6]:
H (X )= lim H∆x (X )= lim |
∑w(xi )∆x log |
|
1 |
|
|
+ |
|
|
||||||||||
|
w(xi ) |
|
|
|||||||||||||||
|
∆x→0 |
|
|
∆x→0 |
|
i |
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
+∞ |
|
1 |
|
|
|
|
|
1 |
|
|||
+ lim log |
∑ |
w(x |
)∆x = |
|
∫ |
w(x)log |
dx + lim log |
. |
||||||||||
|
|
w(x) |
|
|||||||||||||||
∆x→0 |
|
∆x |
i |
|
|
|
|
|
|
|
∆x→0 |
∆x |
||||||
|
|
i |
|
|
−∞ |
|
|
|
|
|
|
|||||||
Первое слагаемое |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
+∞∫w(x)log |
|
1 |
|
dx = h(X ) |
, |
|
|
|
|
|
||||
|
|
|
|
w(x) |
|
|
|
|
|
|||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
||||
представляет собой так называемую дифференциальную энтропию сигнала (или дифференциальную энтропию распределения w(x)). Второе слагаемое стремится к бесконечности совершенно независимо от природы и распределения вероятностей сигнала. Таким образом, при переходе от дискретных значений x к непрерывным энтропия сигнала неограниченно возрастает.
По аналогии с дискретным каналом количество информации, переданной по непрерывному каналу можно представить в следующей форме:
162

I (Y , X )= h(X )−h(X Y )= h(Y )−h(Y X ), |
(4.11) |
где h(X Y ) – условная дифференциальная энтропия сигнала |
x при известном |
сигнале y . |
|
Второе равенство следует из второго свойства количества передаваемой информации (симметрии). Полученное выражение по форме напоминает (4.7), а дифференциальная энтропия играет здесь роль обычной энтропии дискретных сигналов. Однако свойства дифференциальной энтропии существенно отличаются от свойств обычной энтропии. Так, например, h(X ) и h(X Y ) могут быть от-
рицательными.
Дифференциальная энтропия h(X ) уже не представляет собой среднее ко-
личество информации, выдаваемое источником сигнала (для непрерывного сигнала оно бесконечно). Аналогично h(X Y ) не представляет собой количество информации, потерянной в канале, поскольку эта величина тоже бесконечна. Поэтому дифференциальную энтропию следует понимать лишь формально, как некоторую вспомогательную величину полезную при расчетах.
Если помеха аддитивная y = x +n , то нетрудно показать, что
|
|
h(Y |
|
)= +∞∫w(n)log |
|
1 |
|
dn = h(N ), |
|
|
|
|
|
(4.12) |
||||||||
|
|
X |
w(n) |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где w(n) – ПРВ помехи; h(N ) – дифференциальная энтропия помехи. |
|
|||||||||||||||||||||
Подставляя (4.12) в (4.11), находим |
|
|
|
|
|
|
|
|||||||||||||||
( |
)= |
( )− |
|
Y |
|
) |
= |
+∞ ( ) |
log |
1 |
|
|
|
dy |
− +∞ ( ) |
log |
1 |
|
dn |
, |
(4.13) |
|
|
|
|
|
|
|
|
|
|||||||||||||||
I Y , X |
|
h Y |
h( |
X |
|
∫w y |
w(y) |
∫w n |
w(n) |
|
||||||||||||
|
|
|
|
|
|
|
−∞ |
|
|
|
−∞ |
|
|
|
|
|||||||
Найдем дифференциальную энтропию гауссовской помехи с нулевым средним и дисперсией σ2 при отсутствии корреляции между значениями помехи. Согласно (4.12),
|
|
+∞ |
|
|
|
n |
2 |
|
|
|
|
+∞ |
|
log e |
+∞ |
|
|
h(N ) |
= |
∫ |
w(n)log |
|
2πσ2 exp |
|
|
dn = log |
( |
2πσ2 |
)∫ |
w(n)dn + |
∫ |
n2w(n)dn . |
|||
|
|
|
|||||||||||||||
|
|
|
|
2σ |
2 |
|
|
|
2σ |
2 |
|
||||||
|
|
−∞ |
|
|
|
|
|
|
|
−∞ |
|
|
−∞ |
||||
Учитывая +∞∫w(n)dn =1 и |
+∞∫n2w(n)dn =σ2 , получим: |
|
|
|
|
|
|
||||||||||
−∞ |
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
163

h(N )= log( 2πσ2 )+ 1 log e = log2 ( |
2πeσ2 ). |
(4.14) |
2 |
|
|
Дифференциальная энтропия принятого сигнала |
y = x +n с гауссовским |
|
нормальным законом распределения вероятности [6]: |
|
|
h(Y )= − ∞∫w(y)log w(y)dy = log2 |
2πeσy2 . |
(4.15) |
−∞ |
|
|
где σ2y = σc2 + σ2 ; σc2 – дисперсия сигнала. Подставляя (4.14) и (4.15) в (4.13)
получим выражение для определения количества информации, переданной по непрерывному каналу:
|
|
)= |
1 |
|
2 |
+σ |
2 |
|
|
X |
|
|
σc |
|
(4.16) |
||||
|
|
|
|
2 |
|||||
I (Y , X )= h(X )−h( |
Y |
2 |
log2 |
σ |
. |
||||
|
|
|
|
|
|
||||
Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется отношением дисперсии сиг-
нала к дисперсии помехи. Нередко величину называют отношением
сигнал/шум. Чем больше это отношение, тем выше пропускная способность. Последнее вполне естественно, так как если дисперсия сигнала меньше дисперсии помехи или сравнима с ней, то по принятому сигналу трудно судить с определенностью, какое значение сигнала было подано на вход канала.
4.4.3. Пропускная способность непрерывного канала
Пусть сигнал y(t) на выходе канала представляет собой сумму полезного сигнала x(t) и шума n(t), т.е. y(t)= x(t)+n(t), причем x(t) и n(t) статистически не-
зависимы. Допустим, что канал имеет ограниченную полосу пропускания шириной ∆FНК . Тогда в соответствии с теоремой Котельникова (см. п. 1.5) функ-
ции y(t), x(t) и n(t) можно представить совокупностями отсчетов yi , xi , и ni , , где L = 2∆FНКT . При этом статистические свойства сигнала x(t) можно описать многомерной ПРВ w(x1, x2 ,..., xL )= w(x), а свойства шума – ПРВ
w(n1 , n2 ,..., nL )= w(n).
Пропускная способность непрерывного канала определяется следующим
164

образом:
C = lim 1 max I (X ,Y ),
T →∞ T w(x)
где I (X ,Y ) – количество информации о какой-либо реализации сигнала x(t)
длительности T, которое в среднем содержит реализация сигнала той же длительности T , а максимум ищется по всем возможным распределениям w(x).
Когда сигнал на входе канала имеет нормальное распределение и отсчеты независимы величина h(X ) максимизируется [6]. Поэтому пропускная способность гауссовского канала с дискретным временем, рассчитанная на единицу времени, с учетом (4.16) может быть записана в виде
|
VИ |
|
2 |
+σ |
2 |
|
|
VИ |
|
|
2 |
|
|
||
C =VИ I (Y , X )= |
|
σс |
|
|
= |
|
log2 |
(1+h |
). |
(4.17) |
|||||
|
|
|
2 |
|
|
|
|||||||||
2 |
log2 |
σ |
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Полученное выражение показывает, что пропускная способность гауссовского канала с дискретным временем определяется числом импульсов, передаваемых в секунду, и отношением сигнал/шум ( h ).
С учетом взаимосвязи скорости передачи информации и полосы частот непрерывного канала от (4.17) можно перейти к формуле Шеннона, которая устанавливает связь пропускной способности гауссовского канала с полосой пропускания непрерывного канала и отношением мощности сигнала к мощности помехи:
|
C = ∆FНК log2 (1+h2 ). |
(4.18) |
||
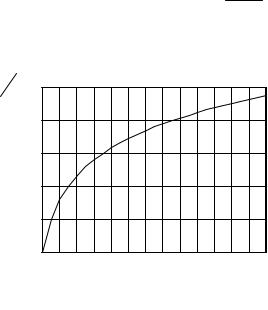
График отношения |
|
C |
= log2 (1+h2 ) изображен на рис. 4.6. Заметим, что |
|
|
∆F |
|||
|
|
|
|
|
|
|
НК |
|
|
при малом отношении h2 <<1
C∆FНК 1,442 h2 ,
апропускная способность канала связи прямо пропорциональна этому отноше-
нию.
При большом отношении h2 >>1 в (4.18) можно пренебречь единицей и считать, что
165
|
C |
≈ log2 (h2 ), |
|
|
∆F |
|
|
|
НК |
|
|
т.е. зависимость пропускной способности непрерывного канала от отношения |
|||
C |
∆FНК |
|
сигнал/шум логарифмическая. |
|
|
Пропускная способность канала, как |
|
|
|
|
|
|
|
|
предельное значение скорости безоши- |
|
|
|
бочной передачи информации, является |
|
|
|
одной из основных характеристик любого |
|
|
h2 |
канала. |
|
|
|
Определим пропускную способность |
|
|
|
стандартного канала тональной частоты, |
имеющего границы эффективно передаваемых частот 0,3...3,4 кГц, среднюю |
|||
мощность сигнала на выходе 56 мкВт при средней мощности помехи |
|||
69000 пВт. |
|
|
|
|
Согласно (4.18), при заданных параметрах |
||
|
|
|
56 10 |
−6 |
|
|
[бит/с]. |
CНК |
= 3,1 103 log2 |
|
|
|
= 3,0 104 |
||
|
|
||||||
|
|
69 10−12 |
|
|
|
||
Для непрерывных каналов справедлива теорема Шеннона, согласно которой сообщения дискретного источника могут быть закодированы и переданы по непрерывному каналу так, что вероятность ошибочного декодирования принятого сигнала y(t) будет меньше наперед заданной положительной величины pош , если производительность источника H ′(X ) меньше пропускной способно-
сти C непрерывного канала.
Для типовых непрерывных каналов многоканальной связи основные технические характеристики и пропускная способность, вычисленная по формуле Шеннона (4.18), при отношении сигнал/шум 20 дБ, приведены в табл. 4.4.
Зная пропускную способность канала и информационные характеристики сообщений (табл. 4.5), можно определить, какие сообщения (первичные сигналы) можно передавать по заданному каналу.
166
|
|
Таблица 4.4 |
|
Характеристики типовых каналов многоканальной связи |
|||
|
|
|
|
Наименование |
Границы |
Пропускная |
|
канала |
передаваемых частот, Гц |
способность, бит/с |
|
Тональной частоты |
300...3400 |
20,64·103 |
|
Предгрупповой широкополосный |
12,3·103...23,4·103 |
73,91·103 |
|
Первичный широкополосный |
60,6·103...107,7·103 |
313,6·103 |
|
Вторичный широкополосный |
312,3·103...551,4·103 |
1,59·106 |
|
Третичный широкополосный |
812,3·103...2043,7·103 |
8,2·106 |
|
Таблица 4.5
Производительность источников сообщений
|
Характер |
Параметры АЦП |
|
Производи- |
||
Вид сообщения |
fd , Гц |
N = log2 |
L |
тельность, |
||
сообщения |
||||||
|
бит/с |
|||||
|
|
|
|
|
||
Телеграфные, 50 Бод |
дискретные |
– |
– |
|
30…50 |
|
|
|
|
|
|
|
|
Телефонные |
непрерывные |
8·103 |
8 |
|
64·103 |
|
Звукового вещания: |
|
24·103 |
|
|
240·103 |
|
первого класса |
непрерывные |
|
|
|||
высшего класса |
непрерывные |
32·103 |
13 |
|
416·103 |
|
Факсимильные, 120 строк/с: |
|
2,93·103 |
|
|
11,72·103 |
|
полутоновые |
непрерывные |
4 |
|
|||
штриховые |
дискретные |
– |
– |
|
2,93·103 |
|
Передача данных, 2400 Бод |
дискретные |
– |
– |
|
2,4·103 |
|
Телевизионные |
непрерывные |
13·106 |
16 |
|
208·106 |
|
Например, первичный |
сигнал |
телевизионного |
вещания имеет |
|||
H ' (Х) = 208 106 бит/ c (табл. 4.5) и поэтому не может быть передан ни по одному из типовых непрерывных или цифровых каналов без потери качества. Следовательно, для передачи сигнала телевизионного вещания требуется создание специальных каналов с более высокой пропускной способностью или снижение скорости цифрового потока.
Контрольные вопросы
1.Какие свойства дискретного сообщения позволяют представить его с помощью сигнала имеющего меньшую избыточность?
2.Определите пропускную способность двоичного телеграфного канала,
167
если скорость передачи в нем 125 бит/с и вероятность ошибки 10-4. Насколько отличается пропускная способность этого канала от идеального?
3.Аппаратура формирует шесть сообщений (символов) алфавита A со следующими вероятностями p(a1 )= 0,22 ; p(a2 )= 0,31; p(a3 )= 0,18 ; p(a4 )= 0,09 ; p(a5 )= 0,05 ; p(a6 )= 0,15 . Постройте сжимающий код методом Шеннона-Фано
(Хаффмена).
4.Почему дифференциальная энтропия источника непрерывных сообщений отличается от энтропии источника дискретных сообщений?
5.Определите пропускную способность стандартного канала тональной частоты, имеющего границы эффективно передаваемых частот 0,3…3,4кГц, среднюю мощность сигнала на выходе 32 мкВт при средней мощности помехи
87000 пВт.
168
ГЛАВА 5. ТЕОРИЯ КОДИРОВАНИЯ СООБЩЕНИЙ 5.1. Помехоустойчивое кодирование: блочные и непрерывные
коды
Решение задачи выбора (отыскания) кода, оптимального по тому или иному критерию, составляет суть теории кодирования. Заметим, что современные методы кодирования не позволяют близко подойти к потенциальной пропускной способности канала связи при одновременно высокой верности передачи. Однако грамотный выбор кода позволяет, во многих случаях, значительно снизить вероятность ошибочного приема при скорости передачи порядка 10 ÷50 % пропускной способности канала.
В настоящее время повышение достоверности передачи в каналах с помехами, осуществляется с помощью кодов, позволяющих обнаруживать или исправлять ошибки. Такое кодирование называется помехоустойчивым. При этом избыточность кодовой последовательности выше, чем избыточность источника сообщений. Благодаря этому и оказывается возможным обнаружение и исправление ошибок приема.
5.1.1. Постановка задачи помехоустойчивого кодирования
Кодирование называется процесс преобразования сообщений в комбинации из дискретных сигналов. Основными задачами, решаемыми кодированием в процессе передачи сообщений, являются:
согласование источника сообщений с каналом по объемам алфавитов; повышение скорости передачи информации по каналу за счет устранения
избыточности в последовательности сообщений; повышение помехоустойчивости передачи информации.
Первые две задачи решаются в кодере источника сообщений. Третья задача решается в кодере канала.
Для постановки задачи помехоустойчивого кодирования обратимся к структурной схеме канала электрической связи (рис. 5.1).
В общем случае в системе электрической связи можно передавать самые
169

различные по физической природе сообщения: цифровые данные, полученные от ЭВМ, речь, тексты телеграмм, команды управления, результаты измерений различных физических величин. Естественно, что все эти сообщения предварительно должны быть преобразованы в электрические колебания, сохраняющие все свойства исходных сообщений, а затем унифицированы, т.е. представлены в форме, удобной для последующей передачи.
Множество возможных дискретных сообщений источника C , должно при этом обладать следующими свойствами:
оно должно быть конечным; все сообщения равновероятны.
Тем самым обеспечивается максимальная энтропия источника (т.е. кодирование источника выполнено наилучшим образом).
Под источником информации на рис. 5.1 понимается устройство, в котором выполнены все названные ранее операции.
C |
|
′ |
|
′′ |
~ |
|
C′′ C |
C |
C |
||||
|
|
Для более экономного использования линии связи, а также для уменьшения влияния различных помех и искажений передаваемая от источника информация может быть в дальнейшем преобразована с помощью кодирующего устройства. Это преобразование, как правило, состоит из ряда операций, включающих учет статистики поступающей информации для устранения избыточности (статистическое кодирование) реализуемое в кодере источника, а также введение дополнительных элементов для уменьшения влияния помех и искажений (помехоустойчивое кодирование) – кодер канала.
В результате ряда преобразований на выходе кодирующего устройства образуется последовательность элементов, которая с помощью модулятора преобразуется в форму, удобную для передачи по линии связи. Среда распространения – это среда, по которой происходит передача сигналов от передатчика (модулятора) к приемнику (демодулятору).
170
