241
служат элементы поля GF(2m ), а не 0 и 1, как у соответствующих многочленов двоичных кодов. Получение кодовых слов с помощью порождающей матрицы означает не простое суммирование строк матрицы, а, как уже указывалось, суммирование базисных векторов, умноженных на различные элементы поля
GF(2m ).
Проверочная матрица кода РС есть проверочная матрица кода БЧХ длины N , являющаяся частью матрицы ДПФ последовательностей с компонентами из поля GF(2m ).
Особенности декодирования кодов РС по сравнению с двоичными кодами БЧХ связаны с тем, что вектор ошибки имеет компоненты εi из поля GF(2m ).
Поэтому при декодировании кодов РС недостаточно указать номера искаженных символов, надо еще определить, насколько искажены символы, т.е. найти значения εi вектора ошибки. Последнее требование усложняет процедуру деко-
дирования кодов РС по сравнению с декодированием двоичных кодов БЧХ. Пример 5.14. Пусть имеется код РС, исправляющий одиночные, двойные и
тройные ошибки. Корнями порождающего многочлена являются элементы α,α2 ,α3 ,α4 ,α5 ,α6 , где α – примитивный элемент поля GF(24 ), образованного с помощью неприводимого полинома p(x)= x4 + x +1 (см. 5.3.5). Спектральные ко-
эффициенты ДПФ кодовых слов в точках αi , i =1,2,...,6 , равны 0. Параметры
кода: N =15 , K = 9 , δ = D0 = N −K +1 = 7 , qИС = 3 .
Так как синдром не зависит от передаваемого слова S , то для рассмотрения процедуры декодирования достаточно задать вектор ошибки E . Допустим,
что многочлен, описывающий вектор ошибки, |
E(x)=α7 x3 +α11x10 , |
т.е. произошла |
двукратная ошибка, исказившая в слове S = (s0s1s2 ...s14 ) символы |
s3 и s10 , при- |
чем принятые символы y3 = s3 +ε3 = s3 +α7 , |
y10 = s10 +ε10 |
= s10 +α11 остальные – |
yi = si . |
|
|
|
|
|
|
|
|
|
€ |
, а за- |
Декодер по реализации Y должен найти оценку вектора ошибки E |
€ |
€ |
€ |
€ |
€ |
= S , и |
тем оценку переданного слова S |
=Y + E . Если оценка E = E , то S |
= S + E + E |
ошибка исправляется. Если |
€ |
≠ E , ошибка не исправляется. |
E |
GF(2m ).
Процедура нахождения |
€ |
зависит от описания вектора ошибки E . Для |
E |
указания номеров искаженных символов воспользуемся многочленом локаторов ошибок σ(z) (см. 5.5.2). Для двоичных кодов многочлен σ(z) полностью оп-
ределяет вектор ошибки E . В случае кодов над полем GF(2m ), каковыми явля-
ются коды РС, необходимо еще указать значения ошибок εi , что делается с по-
мощью так называемого многочлена значений ошибок Ω(z) |
[3, 26]. Для нахож- |
дения εi требуется знание обоих многочленов σ(z) и Ω(z), так как |
εi = Ω(α−i ) |
−i |
) |
. |
(5.32) |
σ (α |
|
|
|
′ |
|
|
|
|
где i – номер искаженного символа; σ′(α−i ) – формальная производная мно-
гочлена σ(z) в точке αi , которая для кодов, заданных над полями характеристи-
ки 2, содержит только четные степени. Коэффициенты при нечетных степенях производной являются четными числами и обращаются в ноль.
Итак, произвольный вектор ошибки над полем GF(2m ) может быть задан с помощью двух многочленов σ(z) и Ω(z). Отметим, что эти многочлены опреде-
лены с точностью до постоянного множителя β – элемента поля Многочлен βσ(z) имеет множество корней, совпадающее с множеством корней многочлена σ(z), и следовательно, оба определяют одни и те же номера иска-
женных символов.
Главная задача декодера состоит в оценке многочленов σ(z) и Ω(z). Если эти оценки правильно описывают реальную ошибку, т.е. множества корней о σ€(z) и σ(z) совпадают, то такая ошибка исправляется. В противном случае ис-
правления не произойдет.
Многочлены локаторов σ(z), значений ошибок Ω(z) и синдрома C(z) свя-
заны ключевым уравнением [26, 30]:
σ(z)C(z)≡ Ω(z)mod(z2qИС ). |
(5.33) |
Трудность решения этого уравнения состоит том, что в соответствии с принципом максимального правдоподобия должны быть найдены многочлены
σ€(z) и Ω€(z) минимальных степеней, причем степень σ€(z) должна быть больше
степени Ω€(z), но менее степени qИС .
Разработаны различные методы решения ключевого уравнения, некоторые из которых уже упоминались в третьем разделе.
Заданная в примере конфигурация двукратной ошибки в соответствии с (5.29) описывается многочленом локаторов, имеющим корни, обратные элементам α3 и α10 :
σ(z)= β(1−α3 z)(1−α10 z)= β(1+(α3 +α10 )z +α3α10 z2 )= β(1+α12 z +α13 z2 ).
Напомним, что вычисления производятся в поле GF(24 ), пример которого дан в табл. 5.2. Сложение удобно выполнять, используя полиномиальное или векторное представление элементов поля, а умножение – степенное представление. Поэтому α3 +α10 =1000 +0111 =1111 =α12 .
Этапы декодирования данного кода при сделанных предположениях о характере искажении описываются следующими операциями.
Этап 1. По принятой реализации символов Y вычисляются 6 компонентов синдрома C1,C2 ,...,C6 , являющихся коэффициентами ДПФ последовательно-
сти Y . Для заданного искажения E(x)=α7 x3 +α11x10 компоненты синдрома оп-
ределяются по формуле
C j =Y (α j )= E(α j )=α7α3 j +α11α10 j , j =1,2,...,6 .
Используя табл. 5.2 задания элементов поля GF(24 ), находим
C j = E(α)=α7α3 +α11α10 =α10 +α21 =α10 +α6 = 0111+1100 =1011 =α7 .
Читателю предлагается самостоятельно произвести вычисления остальных коэффициентов ДПФ и убедиться, что C2 =α12 , C3 =α6 , C4 =α12 , C5 =α14 ,
C6 =α14 .
Результатом выполнения первого этапа является многочлен синдрома
C(z)=α14 z5 +α14 z4 +α12 z3 +α6 z2 +α12 z +α7 .
Этап 2. Декодер решает ключевое уравнение (5.33) при qИС = 3 , оценивает многочлены σ(z) и Ω(z) с помощью алгоритма Евклида нахождения НОД. Не вдаваясь в детали этого алгоритма, с которыми можно познакомиться в [26], приведем результат решения (5.33):

(z) |
=α |
z |
+α |
|
z |
+α |
|
, |
Ω |
(z) |
=α |
|
z |
+α |
|
. |
σ€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
9 2 |
|
8 |
|
|
11 |
( |
€ |
|
|
|
2 |
|
|
1) |
|
3 |
|
Анализ показывает, |
что |
(z) |
|
|
|
z |
|
|
z |
|
|
|
|
(z), т.е. в данном |
|
|
|
σ€ |
|
|
=α−4 α13 |
|
|
2 +α12 |
|
+ |
|
=α−4σ€ |
случае многочлен локаторов определен правильно.
Этап 3. Исправление ошибок производится при сложении символов принятой комбинации Y с компонентами εi вектора ошибки на позициях, номера которых обратны корням многочлена σ€(z). Корни σ€(z) определяются путем
непосредственной подстановки в многочлен всех ненулевых элементов поля
|
|
|
, |
i |
|
0,1,2,...,2 |
|
1 . |
Если |
|
( |
|
) |
|
0 , то предполагается, что искажен символ |
β =α−i |
|
|
|
= |
|
m − |
|
|
|
σ€ |
α−i |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
εi . |
Проделав такую подстановку, найдем корни многочлена |
(z): z |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
. |
|
Действительно, для |
|
элемента |
|
|
: |
|
|
( |
|
) |
|
|
|
|
|
|
σ€ |
|
|
=α−3 |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
=α−10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
−3 |
|
|
|
σ€ α−3 |
|
=α9α−6 |
+α8α−3 |
+α11 = |
|
|
|
+ |
+0110 +1110 = 0000 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
€ |
|
=ε€ |
3 +ε€ |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ε |
|
|
|
|
Для оценки вектора ошибки |
E(x) |
|
3 x |
|
|
|
10 x |
, т.е. для определения |
|
3 |
и |
ε10 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
z |
+α |
|
=α |
|
и с помо- |
найдем производную многочлена локаторов σ (z)= 2α |
9 |
8 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щью формулы (5.32) Получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
€ |
−3 |
|
|
2 −3 |
|
|
3 |
) |
|
|
−9 +α−5 =α6 +α10 =α7 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε€3 = Ω(α |
|
) 8 = (α α |
|
|
+ |
α |
|
8 =α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
) |
|
|
|
α |
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε€ = Ω(α |
−10 |
|
= (α α |
−10 |
+α |
3 |
=α11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
€ |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
α8 |
|
|
|
|
|
|
|
|
|
α8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценка многочлена ошибки |
€ |
|
=ε€ |
3 +ε€ |
10 |
совпадает с E(x), по пред- |
|
|
E(x) |
|
3 x |
|
|
|
10 x |
положению исказившим кодовое слово. Поэтому |
€ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S = S , и двукратная ошибка |
исправлена. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В заключение рассмотрим декодирование данного кода, если кратность |
ошибки больше трех, |
например, |
|
qИС = 4 . Такая ошибка описывается многочле- |
ном локаторов 4-й степени. Декодер, конечно, «не знает» о кратности произошедших искажений и выполняет алгоритм декодирования, предназначенный для исправления ошибок кратности не более 3.
На первом этапе определяется синдром, содержащий по-прежнему 6 компонентов. Синдром ненулевой, так как кратность ошибки меньше кодового
расстояния D0 = 7 , и ошибка кратности 4 обнаруживается. В результате решения ключевого уравнения (если это окажется возможным) будет найден многочлен локаторов, степень которого не превышает 3. Ясно, что множества корней многочленов разных степеней не совпадают (многочлен локаторов не имеет кратных корней). Поэтому корни σ€(z), найденные на третьем этапе декодирования,
будут неправильно указывать номера искаженных символов. Ошибка кратности 4 обнаруживается, но не исправляется.
Коды РС имеют важное теоретическое и практическое значение, так как при заданных N и K имеют максимальное кодовое расстояние, используются для обнаружения и исправления пакетов ошибок и построения высокоэффективных каскадных кодов.
5.6.2. Обнаружение и исправление пакетов ошибок
Основные результаты теории помехоустойчивого кодирования получены в предположении, что передача информации производится по симметричному каналу, для которого постулируется независимость компонентов вектора ошибок как друг от друга, так и от передаваемых символов. Эта удобная модель значительно упрощает теорию кодов, но зато не всегда удовлетворительно отражает процессы передачи информации.
В реальных каналах наблюдаются всплески искажений, причинами которых могут быть, например, коммутационные помехи, быстрые замирания радиосигнала. Чтобы приблизить модель симметричного канала к действительности, вводится понятие пакета ошибок.
Пакетом ошибок длины l называется вектор ошибок E , все ненулевые компоненты которого расположены на отрезке из l подряд следующих позиций, причем в начале и конце отрезка расположены ненулевые компоненты. При l =1 имеем пакет длиной в один символ, т.е. однократную ошибку.
Такая модель пакета в упрощенном виде, без привлечения характеристик коррелированных случайных процессов описывает зависимость отдельных искажений друг от друга. Различают однократные и многократные пакеты в за-
висимости от того, сколько пакетов искажают кодовое слово.
Для обнаружения и исправления пакетов ошибок разработано много способов [33]. Так, для борьбы с пакетами ошибок используется перемежение символов. Оно заключается в том, что символы одного кодового слова на передающей стороне разносятся друг от друга (распределяются по времени) на расстояние, превышающее длину пакета. В образовавшемся промежутке передаются символы других кодовых слов, так что друг за другом следуют символы не одного, а разных кодовых слов.
Пакет ошибок, действуя на qИС подряд следующих символов, тем не менее, искажает только один символ каждого кодового слова. В результате перемежения модель канала с пакетами ошибок трансформируется в модель канала с независимыми ошибками. На приемной стороне символы каждого кодового слова выделяются из принятой последовательности, собираются вместе и декодируются по правилам, рассчитанным на исправление независимых ошибок. Подробно вопросы построения перемежителей рассмотрены в [26]. Здесь же поясним использование кодов РС для обнаружения и исправления пакетов ошибок.
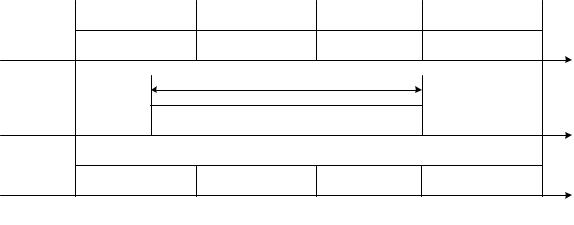
На рис. 5.4 схематично показаны последовательность из |
k = Km |
двоич- |
ных информационных символов ai |
и случайно расположенный, одиночный па- |
кет ошибок длины l . |
|
|
|
|
|
|
a1 |
am |
am+1 |
a2m |
ak−m+1 |
ak |
|
|
|
|
l |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
t |
A1 |
|
|
A2 |
Ak |
|
|
|
|
|
|
|
|
t |
Применение кодов РС, заданных над полем GF(2m ), основано на разбие- |
|
|
|
246 |
|
|
|
l m +1.
A1, A2 ,..., AK
поля
GF(2m )
нии двоичной последовательности на K блоков, содержащих по m двоичных символов. Эти блоки рассматриваются как двоичное представление элементов и, следовательно, кодированию подвергается последовательность информационных символов. Видно, что такое укрупнение уменьша-
ет длину пакета искажений, действующих на символы Ai . Если в двоичной по-
следовательности пакет может исказить l символов, то для символов кода РС максимальная кратность ошибок снижается из-за случайного расположения пакета приблизительно до 
Таким образом, задача обнаружения и исправления пакетов ошибок сводится к использованию кода РС с кодовым расстоянием, позволяющим исправ-
лять ошибки кратности лишь до l m +1. Процедура исправления в этом случае ничем не отличается от исправления независимых ошибок. Для кодов РС также возможно перемежение символов. В отличие от двоичных кодов, когда перемежение соответствует перестановке одиночных двоичных символов, перемежение символов кода РС означает перестановку блоков из m двоичных символов.
5.7. Коды Рида-Маллера 5.7.1. ЗаданиеидекодированиекодовРида-Маллера
Коды Рида-Маллера относятся к линейным двоичным кодам, имеющим большие кодовые расстояния и исправляющим благодаря этому много ошибок. Они пригодны для каналов с малым отношением сигнал/помеха. Этот класс кодов интересен и потому, что с ним связаны многие другие сигналы, применяемые в радиотехнических системах: ортогональные и биортогональные сигналы, симплексные коды, m -последовательности и коды Хэмминга.
Будем рассматривать простейшие коды Рида-Маллера, слова которых являются линейными комбинациями некоторых двоичных функций обладающих полезными для практики свойствами. Сразу укажем, что эти функции выбраны такими, что их отображение в поле действительных чисел дает систему ортого-
vi = 0;1
(v1v2...vm ), где
нальных функций. Это свойство используется при декодировании.
Данное ограничение означает, что в базис кода не входят произведения двоичных функций, т.е. рассматривается код Рида-Маллера 1-го порядка. Некоторые сведения о кодах Рида-Маллера более высоких порядков имеются в [30].
Кодовое слово длины n обычно рассматривается как булева функция (или ее инверсия), заданная в 2m точках, т.е. на наборах из m двоичных элементов. Можно многими способами нумеровать позиции кодового слова m - разрядными двоичными векторами. Ясно, что, как в случае кодов Хэмминга, такая перестановка не влияет на помехоустойчивость получаемых кодов. Будем нумеровать позиции кодового слова числами в двоичной системе счисления
для i =1,2,..., m . Ввиду линейности кодов Рида-Маллера ка-
ждый символ кодового слова Si представим линейной комбинацией
Si = a1v1 + a2v2 +... + amvm ,
или ее инверсией
1 + Si = a01 + a1v1 + a2v2 +... + amvm ,
где a0 , a1, a2 ,...,am – известные информационные символы.
В соответствии с определением порождающей матрицы (5.16) и правилом покомпонентного сложения векторов элементы (1, v1, v2 ,..., vm ) являются столбцами матрицы G . Для m = 3 порождающая матрица размера m +1 = 4 на n =8 имеет вид:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
G = |
0 |
0 |
0 |
0 1 |
1 |
1 |
1 |
. |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
Столбцы матрицы G без верхней строки представляют собой последовательность чисел, записанных в двоичной системе счисления (младшие разряды внизу). Таким образом, столбцы матрицы можно рассматривать как последовательность состояний двоичного суммирующего счетчика:

1
G = Sδ1 , |
(5.34) |
... |
|
Sδm |
|
где 1 – последовательность из единиц; Sδ1 |
– последовательность состояний по- |
следнего (старшего) разряда счетчика; Sδm |
– последовательность состояний |
первого (младшего) разряда. Отметим, что перестановка столбцов и строк порождающей матрицы приводит к эквивалентным кодам.
Кодовое слово есть линейная комбинация базисных векторов (строк матрицы G ):
S = (s1s2 ...sn )= a01+a1Sδ1 +a2Sδ 2 +... +am Sδm . |
(5.35) |
Вид матрицы (5.34) указывает простой способ формирования базисных векторов и получения кодового слова. Схема кодирующего устройства для m = 3 (рис. 5.5) содержит трехразрядный двоичный счетчик, вырабатывающий функции Sδ1, Sδ 2 , Sδ3 , и комбинационную схему, реализующую булеву функцию
(5.35). Естественно, длительность информационных символов, подаваемых в этот кодер, предполагается равной длительности кодового слова, т.е. в данной случае 8 длительностям символов канала.
|
|
|
|
|
Sδ3 |
|
|
a3 Sδ3 |
|
|
|
|
|
|
|
CT |
20 |
|
|
|
|
|
M2 |
|
|
|
& |
|
|
|
|
|
|
|
Sδ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 Sδ2 |
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
S |
|
|
|
Sδ1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
a1 Sδ1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такты |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
a |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
a1 |
a0 |
|
|
|
|
Рис. 5.5. Кодер кода Рида-Маллера длины n=8 |
Двоичный вектор S = (s1s2 ...sn ) с компонентами sш = 0;1 может быть отобра-
жен в вектор W =(w1, w2 ,..., wn ) с действительными компонентами wi = ±1. Для это-
го надо «0» в двоичном векторе заменить на (+1), а «1» – на (–1). Такое отобра-
жение можно определить формулами:
W = (−1)S , wi = (−1)Si . (5.36)
В табл. 5.8 приведены все 16 кодируемых информационных последовательностей и соответствующие им кодовые слова. Обратим внимание, что кодовые слова правой половины таблицы являются инверсией слов левой половины.
Тогда операции суммирования двоичных последовательностей будет соответствовать покомпонентное умножение последовательностей с элементами ±1 . Можно говорить о том, что аддитивная группа двоичных векторов отображается в мультипликативную группу действительных векторов (см. 5.3.2). Конечно, отображение (5.36) не требует для технического воплощения дополнительного оборудования, так как делается разработчиком аппаратуры
Таблица 5.8
Кодовые слова кода Рида-Маллера
Информационные |
Кодовое слово |
|
Информационные |
Кодовое слово |
символы |
|
|
символы |
|
|
|
|
|
|
0000 |
00000000 |
1000 |
11111111 |
|
|
|
|
|
0001 |
01010101 |
1001 |
10101010 |
|
|
|
|
|
0010 |
00110011 |
1010 |
11001100 |
|
|
|
|
|
0011 |
01100110 |
|
1011 |
10011001 |
|
|
|
|
|
0100 |
00001111 |
|
1100 |
11110000 |
|
|
|
|
|
0101 |
01011010 |
|
1101 |
10100101 |
|
|
|
|
|
0110 |
00111100 |
|
1110 |
11000011 |
|
|
|
|
|
0111 |
01101001 |
|
1111 |
10010110 |
|
|
|
|
|
мысленно и связано с разной трактовкой одних и тех же уровней напряжений (высоких и низких) в технических устройствах.
Если применить отображение (5.36) к строкам матрицы (5.34), по определению получим известные функции Радемахера [10]: