Корольов / Теория связи
.pdf
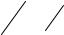
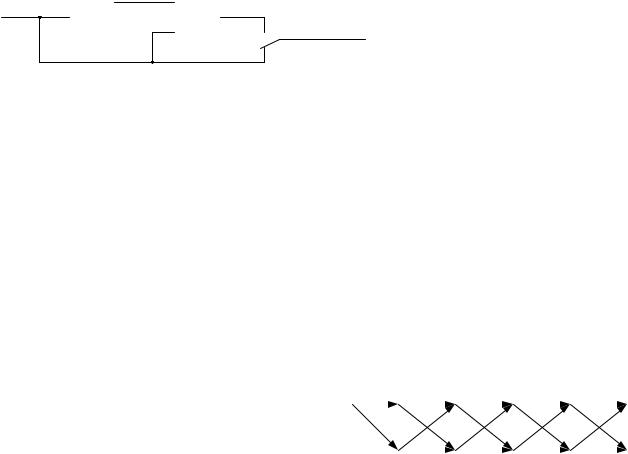

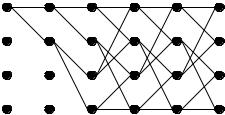

На правой части рисунка видны четыре пути, ведущие в каждый узел решетки. Рядом проставлены расстояния (меры расходимости) этих путей от принятой последовательности на отрезке из 14 блоков. Мера верхнего пути значительно меньше мер нижних. Поэтому можно предположить, что верхний путь наиболее вероятен. Однако декодер Витерби, не зная следующих фрагментов принимаемой последовательности, вынужден запомнить все четыре пути на время приема L элементарных блоков. Число L называется шириной окна декодирования. Понятно, что для уменьшения ошибки декодирования следует выбирать L достаточно большим, в несколько раз превышающим длину блока, что, естественно, усложняет декодер. В данном случае L =15 .
Отметим, что тактика выбора и последующего анализа только одного пути с наименьшим расстоянием составляет сущность более экономного последовательного декодирования [3, 26].
На средней части рис. 5.12 видно, что все пути имеют общий отрезок и, следовательно, прием новых блоков не может повлиять на конфигурацию этого участка наиболее правдоподобного пути. Поэтому декодер уже может принимать решение о значении информационных символов, соответствующих этим элементарным блокам. Поскольку рассматриваемый отрезок составлен из верхних ребер кодовой решетки, то согласно правилу ее построения оценки информационных символов равны 0.
Левая часть рисунка демонстрирует возможную ситуацию неисправляемой ошибки. Существует два пути с одинаковыми мерами расходимости. Декодер может разрешить эту неопределенность двумя способами. Отметить этот участок как недостоверный или принять одно из двух решений: информацион-
267