Корольов / Теория связи

R1 = (−1)Sδ1 , R2 = (−1)Sδ 2 ,…, Rm = (−1)Sδm .

Известно, что всевозможные произведения функций Радемахера образуют полную ортогональную систему функций, которые называются функциями Уолша, и им соответствуют слова кода Рида-Маллера. Ортогональность функций означает, что для двух произвольных функций Уолша Wi и Wj , i ≠ j

скалярное произведение

(Wi ,Wj )= ∑n wik wjk = 0 . k =1

т.е. число позиций, на которых символы последовательностей совпадают, равно числу позиций, на которых последовательности отличаются, и равно поэтому n 2 . Из определения расстояния Хэмминга (см. 5.4.1) заключаем, что кодовое

расстояние кода Рида-Маллера равно n 2 . Отметим, что для пар слов, являю-

щихся инверсией друг друга, расстояние равно n .

Таким образом, коды Рида-Маллера имеют длину n = 2m , m +1 информаци-

онный символ, кодовое расстояние d0 = n 2 = 2m−1 . Отображение двоичных кодо-

вых слов в область действительных чисел ±1 дает множество функций Уолша, включающее 2m функций Уолша Wi , i =1,2,...,n , и 2m противоположных функций i =1,2,...,n . Множество сигналов, составленных из функций Уол-

ша и противоположных им, называется системой биортогональных сигналов. Если в систему не включать противоположные сигналы, то получим систему ортогональных сигналов, которые используются в качестве адресов абонентов в системах множественного доступа с кодовым разделением каналов. Применение ортогональных сигналов в качестве канальных позволяет разделять их в таких системах без взаимных помех [20].

Для кодов Рида-Маллера разработаны достаточно эффективные алгоритмы порогового (мажоритарного) декодирования, изложенные в [30]. Здесь рассмотрим декодирование кодов Рида-Маллера по принципу максимума правдоподобия. Для симметричного канала это совпадает с декодированием по минимуму расстояния между векторами, при котором в качестве оценки переданно-

251

лов в Y и Wj , а n = nc + nнс . При a0 =1, очевидно, получим

Fj1 = 2d (Y,Wj )−n .

Таким образом, оптимальный алгоритм декодирования предполагает следующие этапы:

1.Вычисление 2m коэффициентов корреляции Fj между Y и функциями Уолша Wj , j =1,2,...,2m .

2.Поиск максимального по абсолютной величине коэффициента Fj max .

3.Принятие решения по правилу: a€0 = 0 , если Fj > 0 , и a€0 =1, если Fj < 0 .

Следовательно, данная процедура представляет собой многоканальный корреляционный прием. Ее сложность пропорциональна числу n2 операций сложения и вычитания. Разработаны быстрые алгоритмы декодирования кодов Рида-Маллера, по своей сути аналогичные алгоритмам быстрого преобразования Фурье [30].

5.7.2. Симплексные коды и m -последовательности

Симплексным кодом называется линейный код, порождающая матрица которого равна проверочной матрице кода Хэмминга, т.е. симплексный код дуален к коду Хэмминга [30]. Свое название код получил потому, что его слова,

252

рассматриваемые как многомерные векторы, образуют правильную многомерную фигуру, называемую симплексом.

Так как существует много эквивалентных друг другу кодов Хэмминга, отличающихся перестановкой столбцов проверочной матрицы, то имеется и много эквивалентных симплексных кодов. Среди них есть и код с порождающей матрицей, столбцами которой являются целые числа, записанные в двоичной системе счисления.

Подобная матрица уже рассматривалась в 5.7.1 как часть порождающей матрицы кода Рида-Маллера. Действительно, если в матрице (5.34) исключить первую строку и первый столбец, то получим все 2m −1 ненулевых различных столбцов, т.е. порождающую матрицу симплексного кода. Исключение первой строки, состоящей из единиц, можно трактовать как формирование слов кода Рида-Маллера при a0 = 0 , а исключение первого столбца означает исключение первого (нулевого) символа из слов Рида-Маллера. Таким образом, симплексный код получается из кода Рида-Маллера путем отбрасывания при a0 = 0 перво-

го символа, равного 0 для всех 2m слов (см. левую часть табл. 5.8).

Так как при a0 = 0 множество слов кода Рида-Маллера соответствует ортогональным функциям Уолша, отличающимся друг от друга в 2m−1 позициях, а исключение одинакового для всех слов символа не изменяет расстояния, то отсюда основное свойство симплексного кода: все его слова находятся друг от друга на одинаковом расстоянии, равном 2m−1 . Итак, симплексный код имеет длину n = 2m −1, число информационных символов k = m (на единицу меньше,

чем у кода Рида-Маллера), кодовое расстояние d0 = 2m−1 = n 2 .

В технических приложениях большое значение имеет циклический симплексный код, столбцы порождающей матрицы которого являются степенями примитивного элемента поля Галуа GF(2m ):

Порождающая матрица вида (5.37) указывает простой способ формирования базисных векторов кода путем последовательного умножения элементов

253

поля GF(2m ) на α . Устройства умножения на α представляют собой сдви-

гающий регистр, охваченный линейной обратной связью [10].

Отметим, что помехоустойчивость симплексного кода всегда выше, чем ортогонального, так как при равных кодовых расстояниях слово симплексного кода на 1 элемент короче и, следовательно, энергия, приходящаяся на один символ, больше. Правда, при увеличении m выигрыш уменьшается, стремясь к 0.

На первый взгляд каждая комбинация симплексного кода похожа на случайную последовательность единиц и нулей, из-за чего слова этого кода часто называют псевдослучайными последовательностями (ПСП), m - последовательностями (отмечая связь с параметром кода m ), линейными рекуррентными последовательностями, последовательностями максимальной длины. Все эти названия отражают специфические свойства слов симплексного кода.

ПСП широко используются в радиолокации и радионавигации, в асинхронных системах передачи информации, что обусловлено хорошими корреляционными свойствами этих сигналов.

Перечислим основные структурные свойства m -последовательностей. Рассмотрим бесконечную m -последовательность, получаемую, например, в результате бесконечного умножения элементов поля на α или с выхода генератора m -последовательности.

1. Последовательность удовлетворяет рекуррентному со-

отношению для всех

где hi = 0;1 – известные двоичные числа (коэффициенты минимального много-

члена примитивного элемента поля).

Это свойство следует из того, что генератором m -последовательности является регистр с линейной обратной связью. Символы Sl−1, Sl−2 ,..., Sl−m записаны в

mего ячейках, а Sl есть выход линейной цепи обратной связи.

2.Период m -последовательности равен 2m −1 и максимален по сравне-

254

нию с периодами других последовательностей, получаемых на m -разрядном сдвигающем регистре, но с другим законом функционирования цепи обратной связи.

Это объясняется тем, что степени примитивного элемента α пробегают все 2m −1 ненулевых элементов поля, т.е. все различные m -разрядные векторы.

3. В m -последовательности число единиц равно 2m−1 , а число нулей 2m−1 −1 , что очевидно, так как слово симплексного кода может быть получено путем исключения первого нулевого символа из слов кода Рида-Маллера, у которых число единиц и нулей одинаково и равно 2m−1 . Приблизительно равное соотношение символов 0 и 1 имеет место для отрезка из m символов, взятого в любом месте бесконечной последовательности. Для наблюдателя, не знающего закона формирования последовательности (5.5), появление 0 и 1 происходит примерно с равными вероятностями. Если же рекуррентное соотношение (5.5) известно, то по любому отрезку из m символов можно восстановить все оставшиеся символы последовательности. Этим и объясняется название «псевдослучайная» последовательность.

4. Сумма m -последовательности и ее циклического сдвига есть m - последовательность, удовлетворяющая тому же рекуррентному соотношению, но с другим сдвигом.

Это следует из того, что циклический сдвиг ПСП принадлежит симплексному коду, а сумма кодовых слов линейного кода есть слово данного кода (см. 5.4.1).

Таким образом, симплексный циклический код содержит один нулевой вектор, а остальные 2m −1 являются циклическими сдвигами одной m - последовательности, заданной (5.38). Эти сдвиги, называемые также фазами ПСП, можно пронумеровать различными m -разрядными векторами и сопоставить их с состояниями сдвигающего регистра. Отсюда понятен способ получения ПСП с заданной фазой: в сдвигающий регистр генератора записывается номер фазы, и за и тактов работы генератора формируется требуемая ПСП.

Перейдем теперь к описанию корреляционных свойств сигналов, соответ-

255

ствующих m -последовательностям. Для оценки этих свойств в зависимости от применения сигналов используют периодическую автокорреляционную функцию (ПАКФ), периодическую взаимно-корреляционную функцию (ПВКФ) или непериодические автокорреляционные (АКФ) и взаимно-корреляционные функции (ВКФ).

Так как корреляционная функция определена для последовательностей с действительными компонентами, то далее предполагается, что двоичные символы m -последовательности заменены на +1 и –1 с помощью отображения (5.36). По определению, нормированная ПАКФ бесконечной последовательности S0 , S1, S2 ,..., Sl ,... с периодом n

1 n−1

ρ(τ)= ρ(τ +n)= n ∑j=0 (−1)S j +S j+τ ,

где τ – число тактов сдвига.

После несложных преобразований можно получить

ρ(τ)= (nс −nnнс ),

где nс и nнс – соответственно числа совпадений и несовпадений символов по-

следовательности S и ее циклического сдвига, причем nс + nнс = n . Тогда

т.е. боковые лепестки ПАКФ m -последовательности постоянны и равны

−1n .

Вид ПВКФ m -последовательностей зависит от многих факторов, в том числе и от соотношения между периодами ПСП: периоды равны, взаимно просты или произвольны. Для частных случаев получены или точные, или верхние границы значений взаимно-корреляционных функций. Например, нормированная ПАКФ m -последовательностей с взаимно простыми периодами имеет при любых сдвигах одинаковые значения, равные pс − pнс , где pс и − pнс – соответ-

ственно вероятности совпадения и несовпадения символов двух ПСП. Корреляционные свойства одиночных (непериодических) ПСП также за-

256

висят от многих факторов. Многочисленные исследования показывают, что можно подобрать несколько ПСП или отрезков одной ПСП с удовлетворительными АКФ и ВКФ. Относительно боковых лепестков АКФ одиночных ПСП известно, что их максимальный уровень не превышает 1 n .

Отметим, что m -последовательности являются базовыми для получения других ансамблей сигналов. Так, последовательности Голда, обладающие достаточно хорошими ВКФ, формируются путем сложения двух разных m - последовательностей одинаковых периодов.

Существование разных ПСП одного периода объясняется наличием в конечном поле Галуа нескольких примитивных элементов.

5.7.3. Связь между блочными кодами

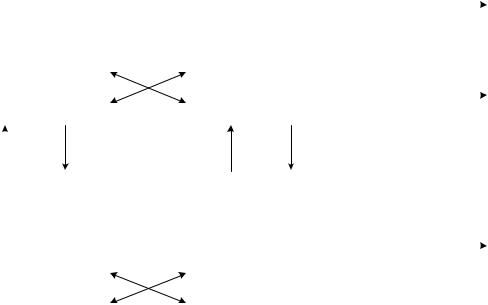
Обобщим вопросы кодирования, изложенные в предыдущих разделах, и поясним связи между некоторыми из рассмотренных кодов, схематично показанные на рис. 5.6. В прямоугольниках указаны длины n , размерности k , кодовые расстояния d0 , обозначены порождающие G и проверочные H матрицы анализируемых кодов. Стрелками указаны операции, с помощью которых можно от одного кода перейти к другому. Эти операции можно рассматривать как способы построения новых кодов из заданных. Перечислим некоторые из таких способов.

Расширение кода означает добавление к кодовому слову проверочного символа, равного сумме всех символов преобразуемого кодового слова. Новый проверочный символ есть общая проверка на четкость. В результате все слова имеют четное число единиц, и кодовое расстояние увеличивается на единицу, если оно были нечетным числом. При четном кодовом расстоянии расширение не увеличивает кодового расстояния, так как для векторов с минимальным четным весом общая проверка на четность равна 0, и вес расширенного вектора не изменяется.

Проверочная матрица расширенного кода Хэмминга образуется путем

257

введения в матрицу H исходного кода нулевого столбца и строки из единиц:

Выкалывание символов является операцией, обратной расширению. Удлинение кода означает добавление в базис кода вектора [1 1 1...1] и

выполнение операции расширения. Порождающая матрица удлиненного кода Gудл может быть записана в виде:

Увеличение числа векторов в базисе означает увеличение размерности кода на 1, а добавление единичного вектора – включение в код дополнительно всех инверсий кодовых слов, что, конечно, не может увеличить минимального расстояния. Понятно, что если кодовое расстояние исходного кода было четным, то в результате удлинения оно не изменится.

Рис. 5.6. Операции над кодами

258

Укорочение кода – операция обратная удлинению. Она состоит в выборе из кода тех слов, у которых первый символ равен 0, и последующему исключения этого равного для всех слов символа.

Из рис.5.6 видно, что расширенный код Хэмминга и код Рида-Маллера, а также код Хэмминга и симплексный код дуальны, так как проверочные матрицы H первых кодов в каждой паре являются порождающими G для вторых и наоборот.

При замене двоичных символов 0 на (+1), а 1 на (–1) совокупность слов Рида-Маллера преобразуется в множество биортогональных сигналов, включающее все функции Уолша и противоположные им. Если при замене двоичных символов ограничиться подпространством кода Рида-Маллера при a0 = 0 , то получим множества ортогональных сигналов. Применение указанной замены двоичных символов на (+1) и (–1) в ненулевых словах симплексного кода дает m -последовательности разных сдвигов.

5.8. Сверточныекоды 5.8.1. Основные параметры

Сверточные коды относятся к непрерывным рекуррентным кодам. Они называются непрерывными, так как последовательность информационных символов при кодировании не разбивается на блоки. Теоретически проверочные символы могут зависеть от неограниченно удаленных информационных. Это позволяет считать сверточные коды обобщением блочных.

Рекуррентными эти коды называются потому, что соотношения, связывающие проверочные символы с информационными, справедливы для любого участка информационной последовательности. В сверточных кодах так же, как и в блочных, выделяют классы систематических и несистематических кодов. Напомним, что в словах систематического кода известны позиции с информационными и проверочными символами.

Термин «сверточные коды» объясняется тем, что кодовое слово можно рассматривать как свертку отклика линейной системы (кодера) и входной ин-

259

формационной последовательности. Поэтому сверточные коды являются линейными, для которых сумма любых кодовых последовательностей также является кодовой последовательностью.

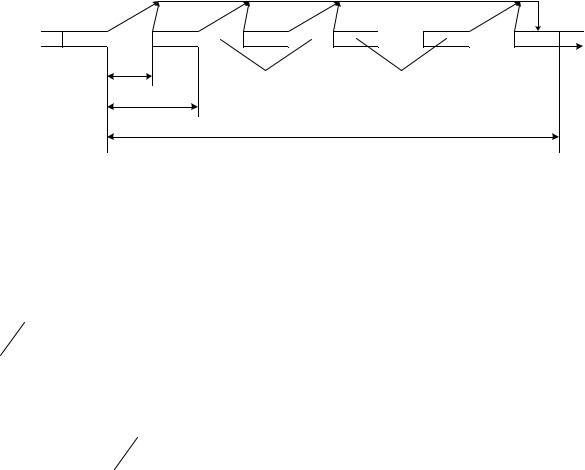
Структура слова систематического сверточного кода схематично изображена на рис. 5.7.

Не заштрихованные участки отмечают позиции, на которых расположены информационные символы (кадры), а заштрихованные – позиции с проверочными символами. Таким образом, кодовое слово состоит из элементарных блоков длиной n0 с k0 информационными символами, что обеспечивает скорость

k0 n0 . При анализе сверточных кодов удобно считать, что информационные

символы, стоящие на одинаковых позициях в элементарных блоках, принадлежат одной информационной последовательности. Таким образом, при исполь-

зовании кода k0 n0 производится кодирование k0 информационных последова-

тельностей, которые формируются, например, путем периодического подключения источника информации на k0 входных шин кодера.

Стрелками на рис. 5.7 условно показаны связи между проверочными и информационными символами. Эти связи имеют место для любого участка кодовой последовательности. Поскольку технически реализация кодеров возможна при ограниченном объеме запоминающих устройств, то влияние информационного символа на проверочные распространяется также на конечное число позиций.

260