Корольов / Теория связи
.pdf
Условная энтропия характеризует среднюю степень неопределенности
принимаемых сигналов, обусловленную действием помех. |
|
|
|
|
|
|
|
||||||||||||
При сопряжении входа канала с любым источ- |
|
y |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
1 |
x1 |
|
|
ником двоичной информации на вход могут поступать |
x1 |
|
|
|
|
y1 |
|||||||||||||
y |
2 |
|
|
|
|||||||||||||||
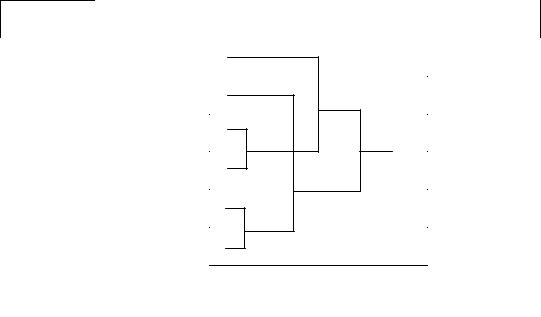
двоичные символы x1 и |
x2 с вероятностями p(x1 ) |
и |
|
p |
|
|
|
|
|||||||||||
|
|
|
x1 |
|
|
||||||||||||||
(1 − p(x1 )) |
соответственно (рис.4.3). На выходе канала |
|
|
|
|
|
|
|
|||||||||||
появляются двоичные символы |
y1 |
и |
y2 . Обозначим |
|
y |
|
|
|
|
||||||||||
вероятность |
ошибки при |
передаче |
любого символа |
|
p |
1 |
|
|
|
|
|||||||||
x2 |
|
|
x2 |
|
y2 |
||||||||||||||
через |
pош . |
Тогда, |
y |
|
|
y |
2 |
|
|
|
а |
y2 |
|
|
|||||
|
|
|
|
|
|||||||||||||||
p 1 |
x |
|
= p |
|
x |
|
=1− pош , |
|
p |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x2 |
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
p y1 x2 = p y2 x1 = pош . В общем случае, для m -ичного дискретного канала [5]:
y j |
|
p |
|
|
i ≠ j, |
|
||
|
|
|
|
ош |
при |
. |
||
p |
|
= |
m |
−1 |
|
|
||
|
xi |
|
|
|
|
|||
|
|
|
− pош |
при i = j. |
|
|||
|
|
1 |
|
|||||
Тогда «шумовая» энтропия будет определяться выражением [5]:
|
|
m |
|
m |
y |
|
|
|
|
1 |
|
|
|
|
||
H (Y X )= ∑p(xi )∑p |
|
j |
x |
log2 |
|
|
|
|
|
= |
||||||
|
|
y j |
|
|
|
|||||||||||
|
i=1 |
|
j=1 |
|
|
|
i |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
p |
xi |
|
(4.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= −(1− p |
|
) log |
|
(1− p |
|
)− p |
|
log |
|
pош |
. |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
ош |
|
2 |
|
ош |
|
|
ош |
|
2 m −1 |
|
|
||||
Из полученного выражения следует, что энтропия определяемая только помехой не зависит от вероятности p(xi ) появления символов на входе канала.
Если символы на входе канала выбираются независимо от предыдущих символов с одинаковыми вероятностями, то энтропия выходных символов достигает своего максимального значения, равного: H (Y )= log2 m .
Таким образом, количество информации, переданной по каналу, это разность между энтропией на выходе и энтропией шума:
I (Y , X )= H (Y )− H (Y |
X |
)= log2 m +(1− pош ) log2 (1− pош )+ pош log2 |
pош |
. |
(4.7) |
|
|||||
|
|
m −1 |
|
||
Количество информации, переданной по каналу связи, обладает следующими основными свойствами:
151