
Корольов / Теория связи
.pdf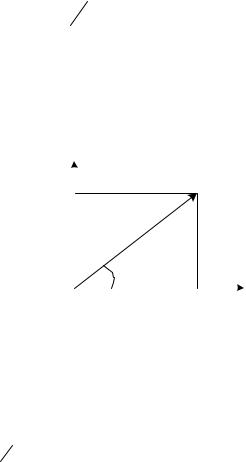
Ее обозначают ~( ) и называют сигналом, сопряженным по Гильберту с
S t
S(t) [6, 20]:
S (t) |
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
0 |
|
]= |
|
|
|
|
|
|
|
|
||
= Im S(t)= ∑Im[(ak − jbk )e |
|
|
|
t |
|
|
|
|
|
|
|
|
|||||||||||||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
jkω |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.56) |
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= ∑(−bk cos kω0t + ak sin kω0t),0 < t <T. |
|
|
|
|
|
|
|
||||||||||||||||||||
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда видно, что сопряженный сигнал можно получить из исходного, |
|||||||||||||||||||||||||||
повернув начальные фазы всех его составляющих на |
−π |
2 |
или, другими слова- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ми, заменив в ряде Фурье (1.71) cos |
на sin , а sin на −cos . |
|
|
|
|
||||||||||||||||||||||
В соответствии с (1.54), (1.55) и (1.56) аналитический сигнал может быть |
|||||||||||||||||||||||||||
выражен через реальный и сопряженный сигналы следующим образом: |
|||||||||||||||||||||||||||
|
|
|
|
|
S(t)= S(t) |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.57) |
|
||||
|
|
|
|
|
+ jS (t). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Исходя из этого, |
аналитический сигнал в мо- |
|
|
|
Im |
S(t) |
|||||||||||||||||||||
мент времени t может быть представлен точкой на |
~ |
(t ) |
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
комплексной плоскости, если по оси абсцисс от- |
S |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
A(t) |
|
|
|||||||||||||||||||||
кладывать значения реального сигнала |
|
S(t), |
|
|
а по |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
оси ординат - сопряженного с ним сигнала |
|
~ |
|
|
|
|
ϕ(t) |
|
|
||||||||||||||||||
|
S |
(t) |
|
|
|
|
Re |
||||||||||||||||||||
(рис. 1.26). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(t) |
|
|||
В качестве примера рассмотрим гармоническое |
|
|
|
|
|
|
|
||||||||||||||||||||
колебание: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
S(t)= A cosω0t,ω0 |
= |
2π |
. |
|
|
|
|
|
|
|
|
(1.58) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Такой сигнал представляется только одним членом ряда Фурье, так как |
|||||||||||||||||||||||||||
|
a |
1 |
T |
|
|
|
A |
|
|
|
|
|
|
T |
=2π |
ω0 = 0 , |
|
|
|
|
|
|
|||||
S0 = |
0 |
= |
|
∫0 Acos |
ω0tdt = |
|
|
sin ω0 t |
|
|
|
|
|
|
|
(1.59) |
|
||||||||||
2 |
T |
ω0T |
0 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
ak = |
a = A, k =1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.60) |
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0, k > 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
bk = 0 , при любых k . |
|
|
|
|
|
|
|
|
|
(1.61) |
|
|||||||||||
Справедливость (1.60) и (1.61) вытекает из ортогональности функций |
|||||||||||||||||||||||||||
cos kω0t и sin kω0t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В соответствии с (1.56), (1.60), (1.61) сопряженный сигнал: |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.62) |
|
|
|
|
|
|
S (t)= Asinω0t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда аналитический сигнал S(t), соответствующий реальному сигналу |
|||||||||||||||||||||||||||
(9), можно записать следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
S(t)= Acosω0t + jAsin ω0t . |
|
|
|
|
|
|
|
|
|
(1.63) |
|
||||||||||||
61

Точки, отображающие реальный и сопряженный сигналы (рис.1.28), совершают в данном случае гармонические колебания по оси абсцисс и ординат относительно точки 0 по законам, соответственно, косинуса и синуса.
Длина вектора, соединяющего начало координат на рис.1.28 с точкой S(t), отображающей аналитический сигнал [6, 32],
A(t)= S |
2 |
(t)+ S |
(t)= |
A |
2 |
cos |
2 |
ω0t + A |
2 |
sin |
2 |
ω0t = A = const . |
(1.64) |
|||||
|
~2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Угол между вектором S(t) и осью абсцисс |
|
|||||||||||||||||
|
|
|
|
|
|
|
~ |
(t) |
|
~ |
≥ 0 |
|
|
|
||||
|
|
ϕ(t)= arctg |
S |
0, S |
. |
(1.65) |
||||||||||||
|
|
|
|
|
|
|
+ |
~ |
|
|||||||||
|
|
S |
(t) |
|
||||||||||||||
|
|
|
|
|
|
|
π, S |
< 0 |
|
|
||||||||
В рассматриваемом случае для верхней полуплоскости получаем:
ϕ(t)= arctg |
A sin ω0t |
= arcg [tg(ω0t)]=ω0t . |
(1.66) |
|
A cosω0t |
||||
|
|
|
Таким образом, с течением времени точка, отображающая аналитический сигнал S(t), соответствующий гармоническому колебанию (1.58), равномерно вращается по окружности с радиусом с угловой скоростью ω0 . Параметры A(t) и ϕ(t) в данном случае определяют амплитуду и фазу синусоидального сигнала.
Для других сигналов, отличных от гармонических, точка S(t) перемещается на комплексной плоскости по более сложной траектории, отличающейся от круговой.
1.8.2. Огибающая, мгновенная фаза и мгновенная частота узкополосного случайного процесса
Комплексный сигнал (1.57) можно представить в форме [6]:
|
S(t)= A(t)e jϕ(t ) = A(t)cosϕ(t)+ jAsinϕ(t), |
(1.67) |
||||||||||||||||||||
где A(t)= |
S |
2 |
|
~2 |
(t) |
называется огибающей сигнала, |
(1.68) |
|||||||||||||||
|
(t)+ S |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
~ |
|
|
|
|
~ |
|
|
|
|
|
|
|
||
а ϕ(t)= Arg S(t)= arctg |
S (t) |
|
0, S (t)≥ 0 |
мгновенной фазой сигнала. |
|
|||||||||||||||||
|
|
|
|
+ |
~ |
|
|
|
||||||||||||||
S(t) |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
π, S (t)< 0 |
|
|
|
|
|
||||||||
Здесь: |
S(t)= A(t)cosϕ(t); |
|
~ |
|
|
|
|
(1.69) |
||||||||||||||
|
S (t)= A(t)sinϕ(t) |
|||||||||||||||||||||
Функция ϕ(t) называется мгновенной фазой сигнала. |
|
|||||||||||||||||||||
Производная от мгновенной фазы сигнала по времени называется мгно- |
||||||||||||||||||||||
венной частотой сигнала: |
|
|
|
|
|
|
|
|
~′ |
|
|
|
|
|
~ |
|
|
|
||||
|
|
|
|
dϕ(t) |
|
1 |
|
|
|
|
|
|
|
′ |
(t) |
|
|
|||||
|
ω(t)= |
= |
|
|
S (t) S(t) |
− S (t) S |
. |
(1.70) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
(t) |
~2 |
(t) |
|
|||||||||
|
dt |
|
|
|
2π |
|
|
S |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ S |
|
|
|
|
|||||
Например, для гармонического сигнала [6]:
62
ω(t)= |
cosω0t cosω0t ω0 |
A2 |
+sin ω0t sin ω0t ω0 A2 |
= const . |
||||
|
|
A2 t + A2 sin 2 ω0t |
= ω0 |
|||||
|
|
|
|
|
|
|||
В общем случае мгновенная частота изменяется во времени. |
||||||||
Из (1.68) следует, что A(t)≥ S(t), причем равенство достигается в моменты |
||||||||
времени, когда |
~ |
(t)= 0 |
. В этих точках производная A(t) совпадает с производ- |
|||||
S |
||||||||
ной сигнала S(t): |
|
~ |
~′ |
|
|
|
|
|
′ |
|
′ |
′ |
′ |
~ |
|
||
S(t) S (t)+ S (t) S (t) |
(1.71) |
|||||||
A (t)= |
|
S 2 (t)+ S~2 (t) |
; A (t)= S (t) при |
S (t)= 0 . |
||||
|
|
|
~ |
(t)= 0 |
огибающая A(t) |
касается сигнала S(t). |
||
Следовательно, при S |
||||||||
Функция cosϕ(t) называется высокочастотным заполнением сигнала. |
||||||||
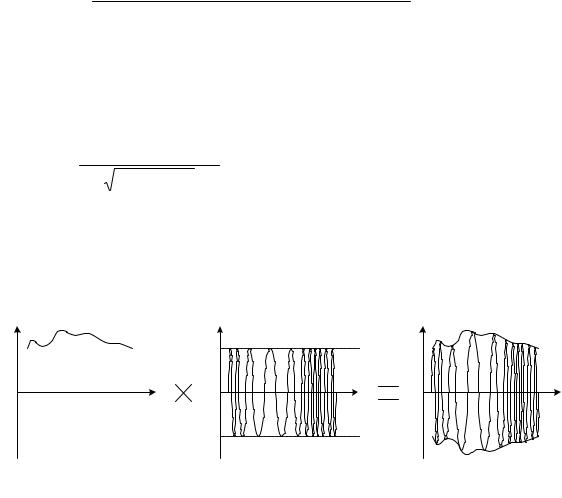
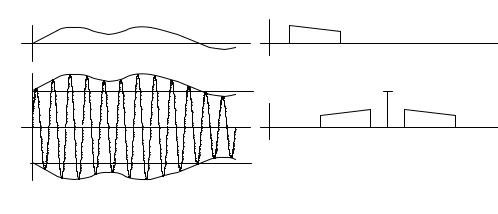
Процесс формирования сигнала на основе огибающей A(t) и фазы ϕ(t) по- |
||||||||
казан на рис. 1.27. |
cos ϕ(t) |
|
|
S(t ) |
|
|||
A(t ) |
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
t |
|
|
t |
t |
|
|
|
|
|
−1 |
|
|
|
|
Если мгновенная частота колеблется вокруг среднего значения ωср , то можно записать:
ϕ(t)= ωcpt +Θ(t); |
(1.72) |
S(t)= A(t)cos[ωcpt +Θ(t)], |
где Θ(t) – называется мгновенной начальной фазой сигнала.
Выражение (1.72) удобно для описания узкополосных сигналов. В этом случае основная часть спектра амплитуд сосредоточена в относительно узкой, по сравнению с ωср , полосе частот. При этом A(t) и ϕ(t) изменяются медленно
по сравнению с cosωсрt . Такие сигналы называются квазигармоническими. У случайных сигналов и помех A(t), ϕ(t), ω(t), ωcp (t) и Θ(t) являются случайными функциями времени.
Контрольные вопросы
1. Что такое информация, сообщение, сигнал? Что общего и в чем отличие между этими понятиями?
63
2.Что такое линия связи, канал связи?
3.Какие радиотехнические устройства обязательно входят в систему электросвязи?
4.Что понимается под аддитивными и мультипликативными помехами?
5.Перечислите известные Вам источники помех. В чем состоит существенное отличие помех от искажений?
6.Постройте спектральную диаграмму разложения в ряд Фурье однополярной периодической последовательности прямоугольных видеоимпульсов с известными параметрами?
7.Как график автокорреляционной функции сигнала характеризует полосу частот, занимаемую сигналом?
8.Источник выдает первичный сигнал s(t), представляющий собой не-
прерывный стационарный случайный процесс, мгновенные значения которого в интервале 0 ÷4 (В) распределены по равномерному закону, а мощность постоянна в полосе частот от 0,3 до 3,4 (кГц):
запишите аналитическое выражение и постройте графики плотности вероятности и функции распределения мгновенных значений сигнала s(t);
определите математическое ожидание M (x) и дисперсию D(x) сигнала
s(t);
определить величину энергетического спектра сигнала.
64
ГЛАВА 2. МЕТОДЫ ФОРМИРОВАНИЯ И ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
2.1. Модуляция сигналов
Формирование модулированных сигналов (модуляция) предполагает взаимодействие двух сигналов: управляющего модулирующего и вспомогательного несущего. Суть управляющего воздействия модулирующего сигнала sc (t) заключается в том, что некоторые параметры γ несущего колебания изме-
няются в соответствии с модулирующим колебанием.
Всистемах связи в качестве управляющих колебаний используются разнообразные первичные электрические сигналы (ПЭС): телефонные, телеграфные, телевизионные и др..
Вкачестве несущих широко применяются гармонические сигналы, собственная частота которых ω0 значительно превосходит верхнюю частоту Ωmax
спектра модулирующего колебания. Это означает, что по отношению к несущему колебанию модулирующее колебание медленно изменяет свои значения во времени. Медленность изменения sc (t) подчеркивает, что на период модули-
рующего колебания приходятся тысячи, сотни тысяч и более периодов несущего колебания. При этом, с одной стороны, обеспечивается достаточно полное отображение модулирующего колебания в несущем колебании, а с другой, обусловливается узкополосность спектра модулированного колебания.
Таким образом, для передачи информации, содержащейся в ПЭС, используется вспомогательное несущее колебание, выполняющее роль переносчика сообщения
Sн(t)= Acos(ωнt +ϕн ), |
ωн = 2πfн . |
(2.1) |
Обычно полагают fн >> k F1 , где F1 |
– наивысшая гармоника ПЭС. |
|
Процесс изменения одного или нескольких параметров высокочастотного (несущего) колебания в соответствии с первичным (модулирующим) сигналом называется модуляцией. Дискретную модуляцию обычно называют манипуля-
65
цией.
При модуляции информационными параметрами несущего колебания Sн(t)= Acos(ωнt +ϕн ) могут быть амплитуда A , частота ωн или фаза ϕн , которые изменяются в соответствии с модулирующим сигналом sc (t), поэтому различа-
ют амплитудную модуляцию (АМ), частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ).
В модулируемых колебаниях изменяемые параметры имеют вид: при амплитудной модуляции – A(t)= A + ∆A(t)= A + asc (t);
при частотной модуляции – ωн(t)=ω0 + ∆ω(t)=ω0 + asc (t); при фазовой модуляции – ϕн(t)=ϕ0 + ∆ϕ(t)=ϕ0 + asc (t);
где ∆Am (t), |
∆ω(t), ∆ϕ(t) |
– приращения, пропорциональные модулирующему |
|||||||
колебанию sc (t); a – коэффициент пропорциональности. |
|||||||||
|
Sн(t ) |
|
|
|
SÌ (sc |
Устройство для получения результирующего |
|||
|
|
|
|
||||||
|
|
|
|
, t ) |
|
||||
|
|
|
|
|
|
|
|
(модулированного) сигнала SМ (Sc ,t) называется |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
модулятором, (рис. 2.1), на один вход которого |
|
|
|
|
|
|
sc (t ) |
||||
|
|
|
|
|
|||||
|
|
|
|
|
подается |
несущее (модулируемое) колебание |
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Sн(t), на |
второй вход первичный (модулирую- |
щий) сигнал sc (t). |
|
|
|||||||
2.1.1. Амплитудная модуляция гармонической несущей
Амплитудная модуляция – процесс изменения амплитуды несущего колебания, соответствующего изменению непрерывного информационного сигнала
[21, 32, 39].
При амплитудной модуляции мгновенная амплитуда несущего колебания:
A(t)= A0 +asc (t), |
(2.2) |
|
где A0 – амплитуда несущей; a |
– коэффициент пропорциональности, выби- |
|
раемый так, чтобы амплитуда A(t) |
всегда была положительной. Частота и фаза |
|
несущего гармонического колебания при AM остаются неизменными.
66
Для математического описания AM сигнала в (2.2) вместо коэффициента a , зависящего от конкретной схемы модулятора, вводится индекс модуляции:
|
mАМ = (Amax − Amin )(Amax + Amin ), |
(2.3) |
т.е. отношение разности между максимальным и минимальным значе- |
||
ниями амплитуд AM сигнала к сумме этих значений. Для симметричного мо- |
||
дулирующего |
сигнала sc (t) AM сигнал также |
симметричный, т.е. |
Amax = Amin = 2∆A . |
Тогда индекс модуляции равен отношению максимального |
|
приращения амплитуды, к амплитуде несущей. |
|
|
|
mАМ = ∆A A0 . |
(2.4) |
Физически индекс модуляции характеризует собой глубину амплитудной модуляции и может изменяться в пределах 0 ≤ mАМ ≤1.
Таким образом для любого AM сигнала справедливо:
SАМ (sc ,t)= A0 [1+ mАМ sc (t)]cos(ω0t +ϕ0 ). |
(2.5) |
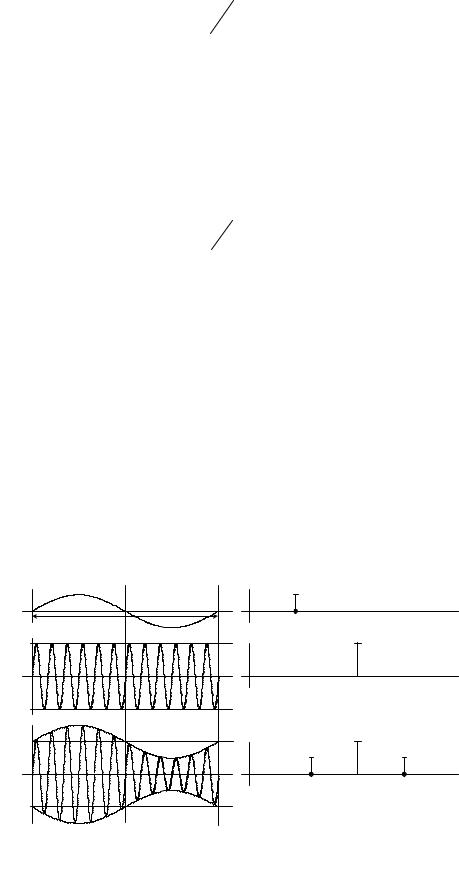
Амплитудная модуляция гармоническим колебанием. В простейшем случае модулирующий сигнал является гармоническим колебанием с частотой Ω <<ω0 . При этом выражение
SАМ (sc ,t)= A0 [1 + mАМ cosΩt]cos(ω0t +ϕ0 ), |
(2.6) |
соответствует однотональному AM сигналу, представленному на рис. 2.26.
Ωс Ω
ω0 ω
ω0 −Ω |
ω0 ω0 +Ω ω |
67
Однотональный AM сигнал можно представить в виде суммы трех гармо-
нических составляющих с частотами: ω0 |
– несущей; ω0 +Ω – верхней боковой |
||||||||||||||
и ω0 −Ω – нижней боковой: |
|
|
|
|
|
|
|
|
|
||||||
S |
АМ |
(s |
,t)= A |
cos(ω |
t +ϕ |
)+ |
A0mАМ |
cos[(ω |
0 |
+ Ω)t +ϕ |
]+ |
|
|||
|
|
||||||||||||||
|
c |
0 |
0 |
0 |
2 |
|
|
0 |
. |
(2.7) |
|||||
|
|
A0mАМ |
|
|
|
|
|
|
|
||||||
+ |
|
cos[(ω0 −Ω)t +ϕ0 ] |
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Спектральная диаграмма однотонального AM сигнала, построенная по (2.7), симметрична относительно несущей частоты ω0 (рис. 2.2,в). Амплитуды боко-
вых колебаний с частотами ω0 −Ω и ω0 +Ω одинаковы и даже при не превышают половины амплитуды несущего колебания A0 .
Гармонические модулирующие сигналы и соответственно однотональный AM сигнал на практике встречаются редко. В большинстве случаев модули-
рующие первичные сигналы sc (t) |
являются сложными функциями времени |
(рис.2.3,а). Любой сложный сигнал |
sc (t) можно представить в виде конечной |
или бесконечной суммы гармонических составляющих, воспользовавшись рядом или интегралом Фурье. Каждая гармоническая составляющая сигнала
с частотой Ωi приведет к появлению в AM сигнале двух боковых составляю-
щих с частотами ω0 ±Ωi .
Ωmin Ωmax
max |
min |
−Ω |
−Ω |
0 |
0 |
ω |
ω |
ω0
ω +Ω 0 min
ω +Ω 0 max
Ω
ω
Множеству гармонических составляющих в модулирующем сигнале с частотами Ωi ,i =1,2,..., N будет соответствовать множество боковых составляю-
щих с частотами ω0 ± Ωi ,i =1,2,..., N . Для наглядности такое преобразование спек-
68

тра при AM показано на рис. 2.3,б. Спектр сложномодулированного AM сигнала, помимо несущего колебания с частотой ω0 , содержит группы верхних и нижних боковых колебаний, образующих соответственно верхнюю боковую полосу и нижнюю боковую полосу AM сигнала.
При этом верхняя боковая полоса частот является масштабной копией спектра информационного сигнала, сдвинутого в область высоких частот на величину ω0 . Нижняя боковая полоса частот также повторяет спектральную диа-
грамму сигнала sc (t), но частоты в ней располагаются в зеркальном порядке от-
носительно несущей частоты ω0 .
Ширина спектра AM сигнала ∆ωAM равна удвоенному значению наиболее высокой частоты спектра модулирующего низкочастотного сигнала, т. е.
∆ωAM = 2Ωmax .
Наличие двух боковых полос обусловливает расширение занимаемой полосы частот примерно в два раза, по сравнению со спектром информационного сигнала. Мощность, приходящаяся на колебание несущей частоты, постоянна. Мощность, заключенная в боковых полосах, зависит от индекса модуляции и увеличивается с увеличением глубины модуляции. Однако даже в крайнем слу-
чае, когда mАМ =1, только 13 всей мощности колебания приходится на две бо-
ковые полосы.
2.1.2. Балансная и однополосная модуляция гармонической несущей
Балансная модуляция
Анализ спектрального состава AM сигнала показал, что первичный модулирующий сигнал находит свое отображение лишь в составляющих боковых полос спектра АМ сигнала. В процессе отображения первичного сигнала в модулированном колебании составляющая спектра частоты ω0 выполняет лишь роль своеобразного начала отсчета для частот боковых спектральных составляющих. Поэтому ее можно исключить из спектра передаваемого сигнала и
69

восстановить па приемном конце.
Если модулированное колебание не содержит составляющей несущей частоты ω0 , то модуляцию называют балансной (БМ). Такой вид модуляции це-
лесообразен с энергетической точки зрения, поскольку на несущую приходится
23 всей мощности модулированного колебания. При прочих равных условиях
высвободившаяся мощность позволит реализовать большую дальность связи, либо при прежней дальности улучшить ее качество.
Однополосная модуляция Балансная модуляция позволяет более рационально распределить энер-
гию сигнала, однако ширина спектра ∆ΩБМ остается такой же, как и для обыч-
ной амплитудной модуляции. В то же время симметрия спектра АМ сигнала означает, что верхняя боковая полоса и нижняя боковая полоса каждая в отдельности, полностью отображают модулирующее колебание. При этом вторая боковая полоса не несет никакой дополнительной информации, вдвое расширяя спектр. Вид модуляции, при котором в спектре амплитудно-модулированного колебания сохраняется лишь одна боковая полоса (верхняя или нижняя), называется однополосной модуляцией.
2.2. Методы угловой модуляции
При фазовой и частотной модуляции сигнал имеет постоянную амплитуду и может быть записан в следующем виде:
SФМ(ЧМ )(t)= A0 cosϕ(t). |
(2.8) |
В отсутствие модуляции аргумент гармонического колебания мгновенная (полная) фаза ϕ(t)=ω0t изменяется с постоянной скоростью ω0, т.е. является ли-
нейной функцией времени. И фазовая, и частотная модуляция предполагают зависимость изменения фазы ϕ(t) от информационного сигнала sc (t). Эта общ-
ность позволяет объединить оба вида модуляции одним названием – угловая модуляция.
При угловой модуляции линейность изменения ϕ(t) нарушается и в каж-
70
