
Корольов / Теория связи
.pdfфона. Такие сигналы часто называются аналоговыми.
Сигналы второго вида - непрерывные по уровню и дискретные по времени (рис. 1.9, б). Дискретизация по времени обычно выполняется путем взятия отсчетов непрерывной по времени функции U (t) в определенные дискретные моменты времени ti ,i =1,2,... . В результате непрерывную функцию U (t) заменяют совокупностью мгновенных значений U (ti ),i =1,2,... . Дискретизация по времени лежит в основе всех видов импульсной модуляции.
Сигналы третьего вида - дискретные (квантованные) по уровню и непрерывные по времени (рис. 1.9, в). Дискретизация значений непрерывной функции U (t) по уровню называется амплитудным квантованием. В результате квантования непрерывный сигнал заменяется ступенчатой функцией. Шаг квантования ∆U (расстояние между двумя соседними разрешенными уровнями) может быть как постоянным, так и переменным. Его обычно выбирают из условий обеспечения требуемой точности восстановления непрерывного сигнала из квантованного.
Сигналы четвертого вида, называемые дискретными (рис. 1.9, г), задаются в определенные дискретные моменты и принимают определенные дискретные значения. Их можно получить, например, из непрерывных сигналов, осуществляя операции дискретизации по времени и квантования по уровню. Такие сигналы легко представить в цифровой форме, т.е. в виде чисел с конечным числом разрядов. По этой причине их называют цифровыми.
Достоинством цифровых сигналов является возможность применения кодирования для повышения помехоустойчивости.
1.3.2. Энергетические характеристики детерминированного сигнала
При передаче радиосигналов главное внимание уделяется передаче информации, а не энергии. Основными энергетическими характеристиками сигнала на интервале t1 ≤ t ≤ t2 , являются мгновенная (текущая) мощность P(t), энергия E и средняя мощность Pcp .
Величина P(t)= S 2 (t) определяет мгновенную мощность сигнала S(t) выделяемой на единичном сопротивлении.
Энергия сигнала, рассматриваемого на интервале времени t1 ≤ t ≤ t2 , является величина
t2 |
t2 |
|
|
E = ∫P(t)dt =∫S 2 |
(t)dt , |
(1.7) |
|
t1 |
t1 |
|
|
31
а средняя мощность сигнала в том же интервале определяется по формуле
|
1 |
t2 |
(t)dt , |
|
|
Pcp = |
t∫S 2 |
(1.8) |
|||
T |
|||||
1 |
|
|
|||
где T = t2 −t1 .
Такие характеристики дают определенное представление о детерминированном сигнале и достаточны для решения целого ряда задач теории связи.
1.4. Представление сигналов в виде рядов ортогональных функций
1.4.1. Разложение сигнала в системе функций
В теории и технике связи нередко приходится встречаться с достаточно сложными по своей форме сигналами и помехами. Для решения многих задач весьма полезно уметь представлять сложные сигналы в виде суммы более простых, хорошо изученных элементарных сигналов, описываемых функциями времени ϕk (t) [6, 32]:
n |
|
S(t)= ∑Ckϕk (t). |
(1.9) |
k=0
Такое представление сложного сигнала в виде линейной комбинации заданных функций называют разложением.
Совокупность коэффициентов разложения {Ck } называют спектром сигнала, а систему функций {ϕk (t)} базисом разложения.
Произведение Ckϕk (t), где ϕk (t) простейший сигнал, а Ck его амплитуда называют спектральной составляющей.
Для того чтобы разложение сигнала (1.9) было выполнимо, базис разложения {ϕk (t)} должен обладать свойством ортонормированности (ортогональности и нормированности).
Две функции S(t) и ϕ(t) ортогональны на интервале t1,t2 , если их скалярное произведение (интеграл от произведения)
t2 |
|
∫S(t)ϕ(t)= 0 , |
(1.10) |
t1 |
|
при том условии, что ни одна из этих функций не равна тождественно нулю при заданных свойствах.
Свойство ортогональности функций обязательно связано с интервалом их определения, т.к. на другом интервале они могут уже быть неортогональны.
Из математики известно, что, если для любой пары функций из ортогональной системы (1.11) выполняется условие
32

t |
ϕi (t)ϕk (t)= 1,i = k; |
|
|
∫2 |
, |
(1.11) |
|
t |
0,i ≠ k, |
|
|
1 |
|
|
|
то данная система функций система функций – ортонормированна (нормированна к 1).
Особое место при решении многих задач в теории связи занимает ряд Фурье, когда в качестве простых ϕk (t) выбирают гармонические колебания.
Представление сигнала s(t) гармоническими функциями имеет следующие преимущества: простое математическое описание; инвариантность к линейным преобразованиям, т. е. если на входе линейной цепи действует гармоническое колебание, то и на выходе ее также будет гармоническое колебание, отличающееся от входного только амплитудой и начальной фазой; как и сигнал, гармонические функции периодические и имеют бесконечную длительность; техника генерирования гармонических функций достаточно проста. Если разложение входного сигнала по ортогональной системе тригонометрических функций известно, то выходной сигнал может быть получен как сумма независимо преобразованных цепью входных гармоник.
1.4.2. Представление сигналов и помех рядом Фурье
Рассмотрим спектральное разложение периодического сигнала. Будем считать, что периодический сигнал определен на бесконечном интервале и может представлен в виде ряда Фурье:
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s(t) = a0 +∑[ak cos(kΩ1t)+bk sin(kΩ1t)], |
|
|
|
|
(1.12) |
|||||||||
|
2 |
k=1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
где k =1,2,... , Ω1 = |
2π |
= 2πF1 |
- частота основной гармоники, F1 = |
1 |
; |
||||||||||||||
T |
T |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
kΩ1 ( k >1 ) – высшие гармоники; ak |
(включая a0 ) и bk |
– коэффициенты Фурье. |
|||||||||||||||||
|
|
2 |
|
T 2 |
|
|
|
|
|
2 |
T 2 |
|
|
|
|
|
|||
ak |
= |
|
−T∫s(t)cos(kΩ1t)dt , |
bk = |
−T∫s(t)sin(kΩ1t)dt |
|
|
(1.13) |
|||||||||||
T |
T |
|
|
||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||||||
Постоянную составляющую (среднее значение) a0 |
2 функции s(t) удобно |
||||||||||||||||||
вычислять по отдельному выражению полученному из ak |
при k = 0 : |
|
|||||||||||||||||
|
|
|
2 T 2 |
|
a |
|
1 T 2 |
|
|
|
|
|
|||||||
a0 |
= |
|
−T∫s(t)dt , тогда |
20 |
= |
|
−T∫s(t)dt , |
b0 |
= 0 |
|
|
(1.14) |
|||||||
T |
T |
|
|
||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
||||||||
Очевидно, что если сигнал представляет собой четную функцию времени u(t) = −u(t) , то в тригонометрической записи ряда Фурье (1.14) остаются только косинусоидальные составляющие ak , так как коэффициенты bk обращаются в
33

нуль. Для сигнала u(t) определяемого нечетной функцией времени, наоборот, в нуль обращаются коэффициенты ak , и ряд содержит синусоидальные составляющие bk
Часто выражение (1.15) удобно представлять в другой, эквивалентной форме ряда Фурье:
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
s(t) = A0 +∑[Ak cos(kΩ1t +Ψk )], |
(1.15) |
|
|
|
|
|
|
k=1 |
|
|
где |
A0 |
= |
a0 |
, |
Ak = ak2 +bk2 - амплитуда, Ψk = −arctg |
bk |
- начальная фаза k - ой |
|
|
2 |
|
|
ak |
|
|
гармоники.
На рис. 1.10 приведены графики, иллюстрирующие представление периодической последовательности прямоугольных импульсов s(t) конечным числом слагаемых ( k = 5 ) ряда Фурье.
Для функции s(t) (рис.1.10) разложение имеет вид
s(t)= |
Am |
+ |
2Am |
sin Ω1t + |
2Am |
sin 3Ω1t + |
2Am |
sin 5Ω1t +.... |
|
(1.16) |
|
|
|
|
|
|
|||||||
2 |
|
π |
3π |
5π |
|
|
|||||
Периодическая последовательность прямоугольных импульсов s(t) пред- |
|||||||||||
ставляется как результат сложения постоянной составляющей |
Am |
и синусои- |
|||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
34
дальных сигналов с частотами F1 ,3F1 ,5F1 ,... , причем период синусоиды с частотой F1 совпадает с периодом последовательности импульсов s(t). Для удобства
F1 можно представить в виде F1 = Ω2π1 = T1 .
Совокупность всех гармонических составляющих разложения функции в ряд Фурье называется спектром функции.
Наличие отдельных гармонических составляющих спектра и величины из амплитуд можно наглядно показать с помощью спектральной диаграммы (рис.1.11), у которой горизонтальная ось служит осью частот, а вертикальная – осью амплитуд.
В точках оси частот F1 ,3F1 ,5F1 ,... отображаются амплитуды соответствующих гармонических составляющих разложения функции.
Легко заметить, что график суммы двух первых слагаемых разложения (1.16) воспроизводит форму графика функции s(t) очень грубо, только в основных чертах. Учет третьего слагаемого существенно улучшает совпадение суммы с функцией s(t). Таким образом, с увеличением числа учитываемых гармоник точность представления s(t) возрастает.
На практике спектральные диаграммы называют более кратко – амплитудный спектр, фазовый спектр. Чаще всего интересуются амплитудным спектром (рис. 1.11). По нему можно оценить процентное содержание гармоник, наличие и уровни отдельных гармонических составляющих спектра.
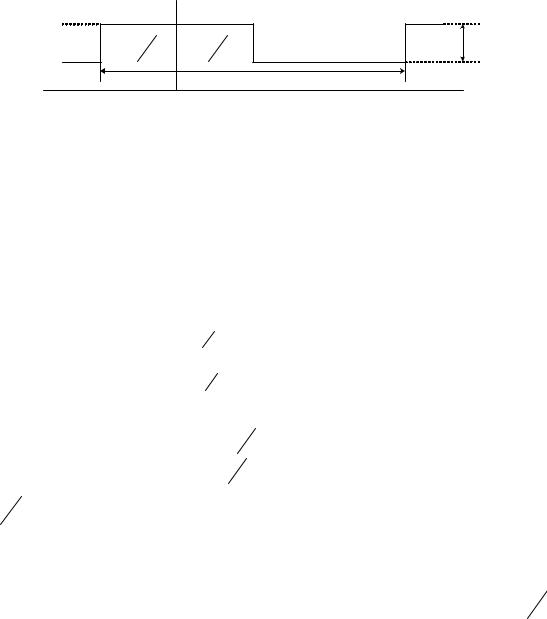
Пример 1.1. Разложим в ряд Фурье периодическую последовательность прямоугольных видеоимпульсов с известными параметрами ( Am , T , τи ) (рис. 1.12), четную относительно точки t = 0 :
A |
|
, −τ и |
|
≤ τ |
и |
< τ и |
|
|
|
||
|
1 |
|
|
2 |
|
|
2 |
. |
|||
s(t) = |
|
|
, |
τ и |
< τ |
|
|
||||
A |
0 |
2 |
и |
≤ T − |
τ и |
2 |
|||||
|
|
|
|
|
|
|
|
||||
35
A1 |
s(t ) |
|
|
|
|
Am |
|
A0 |
− τи 2 |
τи 2 |
|
|
0 |
|
T |
|
|
|
Рис.1.12. Временное представление периодической последовательности прямоугольных импульсов.
Воспользуемся для представления этого сигнала формой записи ряда Фурье в виде (1.12). Для спектрального представления последовательности прямоугольных импульсов начало отсчета целесообразно брать в середине импульса. Действительно, в этом случае и в разложении останутся только косинусоидальные составляющие, так как интегралы от нечетных функций за период равны нулю bk=0.
По формулам (1.14) находим коэффициенты:
a0 |
|
Amτи |
|
Am |
|
2Am |
tи |
|
|
2Am |
|
kΩ1τи |
|
|
= |
= |
, ak = |
∫2 |
cos(kΩ1t)dt = |
sin |
, |
||||||||
2 |
|
|
T |
kπ |
|
|||||||||
|
T |
S |
−tи |
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
позволяющие записать ряд Фурье:
s(t)= |
Am |
|
∞ |
sin(k |
π |
S |
) |
|
|
||
1 |
+ 2∑ |
|
|
|
|
|
cos(kΩ1t) |
, |
|||
|
|
π |
|
|
|
|
|||||
|
S |
= |
k |
S |
|
|
|
|
|
||
|
|
|
k 1 |
|
|
|
|
|
|
||
где S = T τи - скважность импульсной последовательности.
Для построения спектральных диаграмм при конкретных числовых данных полагаем k = 0,1,2,3,... и вычисляем коэффициенты гармоник. Результаты
расчета первых восьми составляющих спектра при Am = 2В , T = 20мс, S = T τи = 2
и 8 сведены в табл. 1.1 и построены спектральные диаграммы на рис.1.13.
Таблица 1.1. Амплитуды спектральных составляющих для периодической последовательности прямоугольных импульсов
|
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
k , Гц |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
|
, В |
|
S=2 |
1 |
1,27 |
0 |
0,42 |
0 |
0,25 |
0 |
0,18 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
S=8 |
0,25 |
0,48 |
0,45 |
0,39 |
0,32 |
0,23 |
0,15 |
0,07 |
0 |
a |
|
||||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
36

Ak |
A1 |
|
|
|
|
Ak A1 |
A3 |
|
|
|
A |
|
|
|
|
A0 |
|
|
|
||
|
|
|
|
|
A5 |
|
|
|||
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
A3 |
A5 |
A7 |
|
|
|
A7 |
|
|
|
|
|
|
|
|
|
|
|||
|
F 3F |
5F |
7F |
F |
F 3F |
5F1 |
7F |
F |
||
|
1 |
1 |
1 |
1 |
|
1 |
1 |
|
1 |
|
Рис. 1.13. Спектральные диаграммы периодической последовательности импульсов: а) - при скважности S=2; б) - при скважности S=8
Из приведенного примера следует, что с увеличением скважности увеличивается число спектральных составляющих и уменьшаются их амплитуды.
Выбор количества спектральных составляющих зависит от формы сигнала и точности его представления рядом Фурье. Плавное изменение формы сигнала потребует меньше числа гармоник при той же точности представления, чем для скачкообразного сигнала. Для приближенного представления прямоугольных импульсов на практике обычно считают, что достаточно трех - пяти гармоник.
1.4.3. Применение преобразования Фурье для непериодических сигналов
Для спектрального представления непериодических (импульсных) сигналов s(t), заданных на конечном интервале ( t1 , t2 ) (рис. 1.14), непосредственно воспользоваться рядом Фурье нельзя. Для гармонического разложения сигнала мысленно дополняют его такими же импульсными сигналами до периодического с некоторым интервалом Т (рис. 1.14).
-
|
s(t) |
|
|
|
sпер (t + T ) |
s(t ) |
sпер (t −T ) |
8 |
T |
|
T |
|
0 t1 |
|
t2 |
|
T |
|
T |
8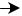
Рис. 1.14. Импульсный сигнал s(t) и его периодическое продолжение sпер(t+kT)
Для того чтобы вне искусственно введенного интервала исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов.
37

В пределе, при увеличении периода Т → ∞ все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность вновь станет одиночным импульсом.
Для вычисления спектра удобна симметричная комплексная форма ряда Фурье, но в нем вместо суммы будет интеграл с бесконечными пределами.
|
1 |
|
∞ |
|
|
|
|
s(t)= |
−∞∫S(Ω)e jΩt dΩ , |
|
(1.17) |
||||
2π |
|
||||||
|
∞ |
|
|
|
|
||
∫s(t)e− jΩt dt . |
|
|
|
|
|||
S(Ω)= |
|
(1.18) |
|||||
|
|
−∞ |
|
|
|
|
|
При таком предельном переходе основная частота сигнала |
Ω1 |
= 2π |
T |
стре- |
|||
|
|
|
|
|
|
|
|
мится к нулю, бесконечно увеличивается число спектральных составляющих, частоты соседних гармоник kΩ1 и (k +1)Ω1 становятся неразличимыми, а спектр будет сплошным.
Формулы (1.17) и (1.18) называются соответственно обратным и прямым преобразованиями Фурье. Они дают взаимосвязь между сигналом s(t) и его
|
|
|
комплексной спектральной плотностью S(Ω). |
|
|
|
Представим спектральную плотность в показательной форме: |
|
|
|
|
|
S(Ω) = S(Ω)e− jϕ(Ω), |
|
где |
|
|
S(Ω) – модуль S(Ω), который называют спектральной плотностью ампли- |
||
туд, или амплитудным спектром; ϕ(Ω) – аргумент |
|
|
S(Ω), называемый фазовым |
||
спектром сигнала. По определению, модуль S(Ω) – |
четная функция частоты, а |
|
аргумент ϕ(Ω) – нечетная функция. |
|
|
|
Пример 1.2. Найти спектральную плотность прямоугольного видеоим- |
|
пульса sв (t) четного относительно t = 0 , длительностью τи и с амплитудой Am
(1.15, а).
Запишем аналитическое выражение для заданного видеоимпульса:
A |
, |
−τи |
2 |
≤ t < |
τи |
2 . |
|
s(t)= m |
|
|
τи |
|
|
||
0, |
|
t > |
2 |
|
|
||
|
|
|
|
|
|
|
|
Тогда спектральную плотность импульса находим по формуле (1.18):
|
tи |
− Ω |
A |
|
|
|
jΩτ |
и |
|
|
jΩτ |
и |
|
|
||
|
|
|
||||||||||||||
s(Ω) = Am ∫e |
j t dt = |
m |
exp |
− |
|
|
− exp |
|
. |
|
||||||
|
|
|
2 |
|
|
|||||||||||
|
−tи |
|
− jΩ |
|
|
2 |
|
|
|
|
||||||
Это выражение с учетом формулы Эйлера sinα = |
|
(e jα −e− jα ) |
можно перепи- |
|||||||||||||
|
2 j |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
38
сать в виде:
|
|
Ωτ |
и |
|
|
|
|
|
sin |
|
2 |
|
|
|
|||
s(Ω) = Amτи |
|
|
|
|
|
. |
(1.19) |
|
|
Ωτ |
и |
|
|
|
|||
|
|
|
|
|
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что спектральная плотность прямоугольного видеоимпульса, четного относительно t=0, вещественная. Фазовый спектр
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
приs > 0 |
. |
|
|
|
|
|
|
|
|
|
|
|
(1.20) |
|||||
|
|
ψ(Ω)= |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
приs < 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассчитанные по формулам (1.19) и (1.20) амплитудный и фазовый спек- |
||||||||||||||||||||
тры |
прямоугольного |
видеоим- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
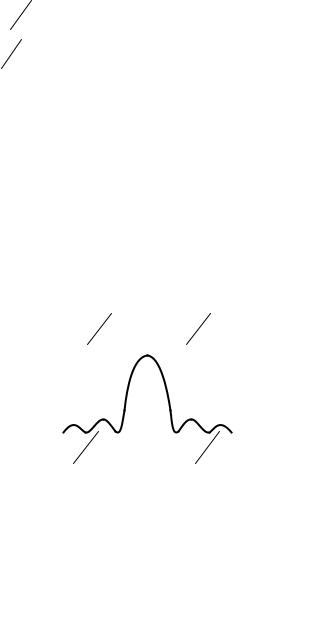
пульса изображены на рис. 1.15. |
|
|
|
|
s(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следует отметить, что нули |
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
амплитудного спектра |
определя- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−τи 2 |
|
|
|
τи 2 |
|
|
|
|
|
|||||||||
ются |
длительностью |
импульса. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
При удлинении импульса рас- |
|
|
|
|
s(Ω) |
|
|
|
|
|
|
|
|
|
|
|
|||||
стояние между нулями s(Ω) со- |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
кращается, что равносильно су- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
жению спектра. При укорочении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
− π τ |
и |
|
|
|
|
π τ |
|
|
Ω |
||||||||||
(сжатии) импульса, наоборот, |
|
|
|
|
|
|
|
|
|
|
|
|
и |
||||||||
|
|
|
ψ (Ω) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
расстояние между нулями функ- |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
||
s(Ω) увеличивается, спектр |
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|||||
расширяется. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Спектральный метод является |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
одним из основных при расчетах линейных электрических цепей. Знание спектра сигнала позволяет правильно
рассчитать и установить полосу пропускания усилителей, фильтров и других элементов каналов связи. Это необходимо для осуществления неискаженной передачи сигнала для обеспечения разделения сигналов и ослабления помех.
1.5. Теорема Котельникова
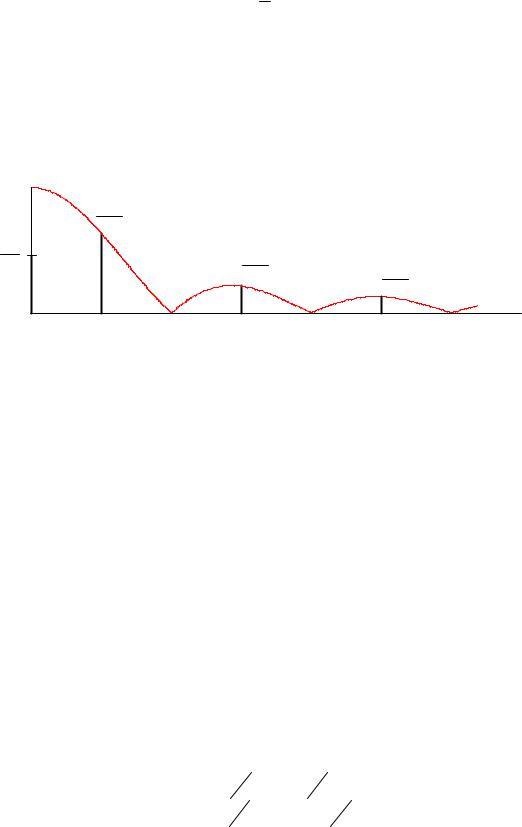
В 1933 году В.А. Котельниковым доказана теорема отсчетов [6, 32], имеющая важное значение в теории связи: непрерывный сигнал s(t) с ограниченным спектром можно точно восстановить (интерполировать) по его отсче-
там s(k∆t), взятым через интервалы ∆t = |
1 |
|
, где F |
– верхняя частота спектра |
|
(2F ) |
|||||
|
|
|
|||
сигнала.
39
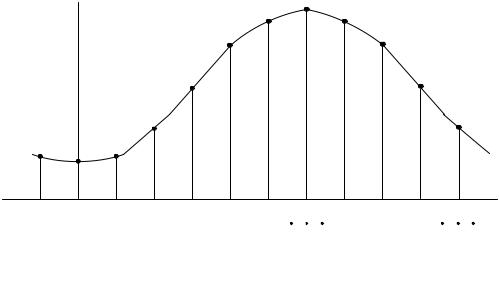
В соответствии с этой теоремой сигнал s(t) можно представить рядом Котельникова [6, 32]:
|
|
|
|
|
|
|
k |
|
|
||
∞ |
|
k |
sin 2πF t |
− |
|
|
|
|
|
||
|
|
|
|
||||||||
|
|
|
|
2F |
|
|
|||||
s(t)= ∑ s |
|
|
|
|
|
|
|
|
. |
(1.21) |
|
|
|
|
k |
|
|||||||
k =−∞ |
|
2F |
2πF |
t − |
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
2F |
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Таким образом, сигнал s(t), можно абсолютно точно представить с помо-
щью последовательности отсчетов |
|
k |
, |
заданных в дискретных точках |
k |
|
s |
|
|
|
|||
|
2F |
|||||
|
|
2F |
|
|
||
(рис.1.16). |
|
|
|
|
|
|
s(t) |
|
|
|
|
|
|
|
|
s(0) |
|
1 |
|
2 |
|
|
k |
|||||||
|
|
s |
|
|
|
s |
|
|
|
s |
|
|
||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2F |
|
2F |
|
|
2F |
|||||||
− |
1 |
0 |
|
2 |
|
4 |
|
k |
|
t |
||||||
|
|
|
|
|
||||||||||||
2F |
|
|
|
2F |
|
|
|
2F |
|
2F |
|
|
|
|||
Функции
|
|
|
k |
|
|
|
|
sin 2πF t |
− |
|
|
|
|
|
|
|
|
|||
ψ(t)= |
|
|
2F |
(1.22) |
||
|
k |
|
|
|||
|
2πF t − |
|
|
|
|
|
|
2F |
|
|
|||
|
|
|
|
|
||
образуют ортогональный базис в пространстве сигналов, характеризующихся ограниченным спектром:
Φ(f )= 0 при |
|
f |
|
> F . |
(1.23) |
|
|
Обычно для реальных сигналов можно указать диапазон частот, в пределах которого сосредоточена основная часть его энергии и которым определяется ширина спектра сигнала. В ряде случаев спектр сознательно сокращают. Это обусловлено тем, что аппаратура и линия связи должны иметь минимальную полосу частот. Сокращение спектра выполняют, исходя из допустимых искажений сигнала. Например, при телефонной связи хорошая разборчивость речи и узнаваемость абонента обеспечиваются при передаче сигналов в полосе час-
40
