Корольов / Теория связи

значение другой функции сохраняется неизменным, что позволяет избежать глубокой паразитной модуляции огибающей.

2.5.3. Принцип частотной модуляции с непрерывной фазой

Частотная модуляция с непрерывной фазой (ЧМНФ) является частным случаем частотной модуляции с минимальным сдвигом. В этом случае фаза манипулируемого колебания изменяется непрерывно и не имеет скачков на границах радиоимпульсов. При ЧМНФ для передачи +1 и −1, как и при обычной двоичной ЧМн, используются две частоты, однако разность частот выбирается такой, чтобы за время длительности элемента T фаза несущего колебания из-

менялась ровно на π 2 .

Как отмечалось ранее, ширина спектра модулированного сигнала S(t) оп-

ределяется видом квадратурных составляющих S2k (t) и S2k +1 (t). Поэтому ширину спектра сигнала с КОФМС можно сократить, если ввести вспомогательную амплитудную модуляцию этих квадратурных составляющих, позволяющую уменьшать значение огибающих колебаний S2k (t) и S2k +1 (t) в моменты скачков фазы этих колебаний на 180°, Вспомогательную амплитудную модуляцию квадратурных составляющих удобно осуществить по гармоническому закону

[5, 13]:

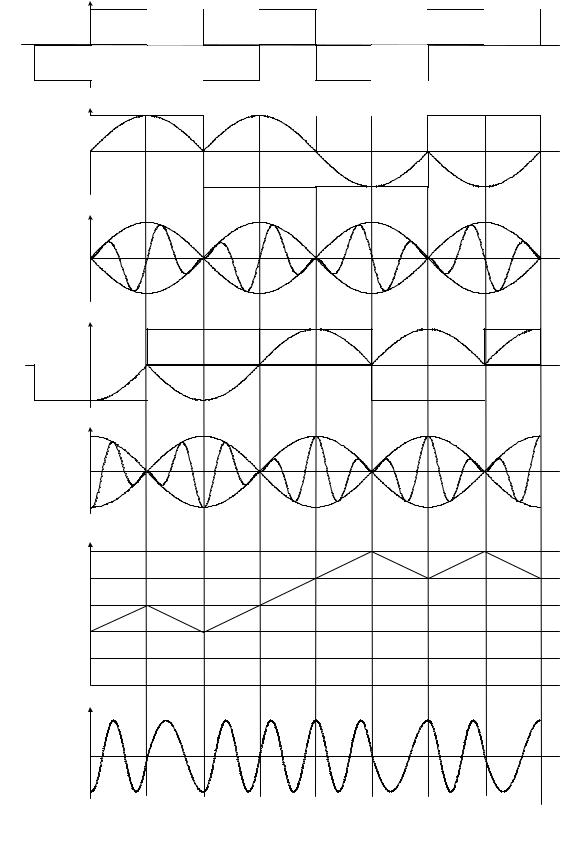
Функции A0 x2k +1 (t)sin πt 2Tc , S2k +1 (t), A0 x2k (t)cos πt 2Tc и S2k (t) показаны для информационной последовательности x(t) изображенной на рис. 2. 30,а. Как следует из (2.38) и рис. 2.30, д, знак функции x2k +1 (t) может меняться лишь в моменты равенства нулю огибающей квадратурной составляющей S2k +1 (t), при-

чем огибающая квадратурной составляющей S2k (t) в эти моменты времени дос-

тигает максимального значения. Соответственно, функция x2k (t) может изме-

нять свой знак лишь в моменты равенства нулю огибающей квадратурной со-

101

ставляющей S2k (t). Этим обеспечивается непрерывность фазы суммарного ко-

лебания S(t) в моменты смены информационных символов, причем на каждом i -м интервале времени [iTc ,(i +1)Tc ] колебание S(t) имеет постоянную огибаю-

щую и одну из двух возможных частот ω0 ± π 2Tc . Действительно, как следует из

(2.38), на рассматриваемом i -м интервале времени:

Таким образом, при условии (2.38) колебание S(t)) представляет собой

последовательность ЧМн сигналов с непрерывной фазой. В отличие от обычной

двоичной ЧМн, когда разнос частот выбирается кратным 1Tc , в данном случае разнос частот существенно меньше и равен 12Tc , что и обусловило название

этого метода – частотная модуляция с минимальным сдвигом (ЧММС).

Закон изменения фазы ϕ(t) колебания (2.39) и сам вид колебания S(t) для

последовательности информационных символов, изображенной на рис. 2.30,а,

показаны на рис. 2.30,е,ж для ω0 = 2π Tc . Как следует из (2.39), мгновенная час-

тота колебания S(t) на i-м интервале времени зависит не от значения xi переда-

102

Спектр последовательности сигналов с ЧММС не зависит от того, как вводится полезная информация в квадратурные составляющие сигнала: раздельно или путем непосредственной манипуляции частоты сигнала в соответствии с передаваемыми информационными символами.

Сигналы с ЧММС являются частным случаем ЧМ – сигналов с непрерывной фазой (ЧМНФ). На интервале [0,Tc ] такой сигнал представляется в виде:

а в общем случае на интервале [kTc ,(k +1)Tc ] :

где m – индекс модуляции.

Контрольные вопросы

1.Представьте временные характеристики передаваемого сообщения, состоящего из последовательности двоичных символов вида 0101011010 в униполярной форме. В форме относительного кода. В биимпульсной форме.

2.Для каких целей используется модуляция в системах электрической

связи?

3.Как вычислить ширину спектра сигналов АМн, ЧМн и ФМн?

4. Задано аналитическое выражение для модулированного сигнала S(t)=12cos(6,28 106 t +5cos12,56 104 t). Определите мощность модулированного

104

сигнала, максимальные девиации частоты и фазы, постройте спектральную диаграмму этого сигнала. Можно ли определить, какой сигнал здесь представлен: ЧМ или ФМ?

5.Представьте временные характеристики сигналов многопозиционной амплитудной и частотной модуляции.

6.Какое свойство функций Бесселя позволяет считать спектр сигналов угловой модуляции ограниченным?

7.Как изменится ширина спектра однотональных АМн и ЧМн сигналов, если частоту модулирующего сигнала увеличить вдвое?

105

ГЛАВА 3. ПОМЕХОУСТОЙЧИВОСТЬ ПРИЕМА ДИСКРЕТНЫХ СООБЩЕНИЙ

Проблема помехоустойчивости является одной из важнейших проблем современной радиотехники. В классической работе основоположника статистической теории связи В.А. Котельникова «Теория потенциальной помехоустойчивости» была сформулирована и решена задача статистического синтеза оптимальных приемных устройств, проанализированы системы связи при различных видах модуляции и определена предельная помехоустойчивость, которая может быть достигнута при заданном способе передачи информации. В дальнейшем теория развивалась не только для гауссовского канала, но и для каналов с переменными параметрами, пространственно-временных каналов, каналов с сосредоточенными и импульсными помехами и др. В настоящее время статистической теории связи посвящена многочисленная литература [5, 21, 32, 39]. При этом результаты теории оказались весьма конструктивными и способствовали быстрому развитию современной техники связи.

3.1. Критерии качества и правила приема дискретных сообщений

3.1.1. Понятие о помехоустойчивости систем электрической связи

Качество передаваемой информации принято оценивать достоверностью передачи сообщений, т.е. степенью соответствия принятого сообщения переданному. Количественная мера достоверности и помехоустойчивости зависит от характера передаваемых сообщений (текст, речь, музыка, изображение и т.

д.).

Для оценки качества приема дискретных сообщений применяется вероятность ошибочного приема переданного символа рош . Значение вероятности ошибки должно быть достаточно малым. Так для систем радиорелейной связи

106

рош имеет порядок 10−6 , для тропосферной связи 10−5 , для радиосвязи 10−3 .

Появление ошибок в системах связи происходит из-за действия помех различных видов. Способность систем связи различать (восстанавливать) сигналы с заданной достоверностью при наличии помех называется помехоустойчивостью. Различают потенциальную и реальную помехоустойчивость. Под потенциальной помехоустойчивостью понимают предельно достижимую помехоустойчивость при заданных сигналах и помехах. Реальная помехоустойчивость систем связи с учетом конкретного выполнения элементов передающего и приемного тракта, линии связи, кодека, модема всегда меньше теоретической.

3.1.2. Задача оптимального приема

Рассмотрим сначала наиболее простую задачу теории обнаружения сигналов. Допустим, что некоторый объект, интересующий наблюдателя, может находиться в одном из двух состояний S0 или S1 . Такими состояниями могут быть, например, наличие или отсутствие цели в зоне действия РЛС, передача сигнала «0» или «1» по каналу связи, работоспособность или отказ устройства и др. В каждом конкретном эксперименте объект находится в состоянии S0 или в состоянии S1 с вероятностями p0 и p1 (p0 + p1 =1) соответственно. Поскольку действительное состояние объекта наблюдателю не известно, то можно лишь выдвинуть предположение (гипотезу) H0 о том, что объект находится в состоя-

нии S0 и альтернативное предположение H1 .

В зависимости от состояния S0 или S1 объекта результаты эксперимента имеют плотность распределения вероятностей (ПРВ) w(y H0 ) или ПРВ w(y H1 ). На основе анализа наблюдений y1 , y2 ,..., yn необходимо опреде-

лить, в каком именно состоянии находится объект.

В этих терминах задача состоит в том, чтобы на основе наблюдении y

проверить справедливость гипотезы H0 . Любое правило проверки гипотезы ка-

ждому конкретному результату эксперимента y должно поставить в соответст-

107

вие определенное решение. Но это означает, что при заданном правиле реше-

ния среди всех возможных исходов y G можно выделить область G0 , где при-

нимается гипотеза H0 . Если же результат наблюдения y G0 , то принимается решение H1 .

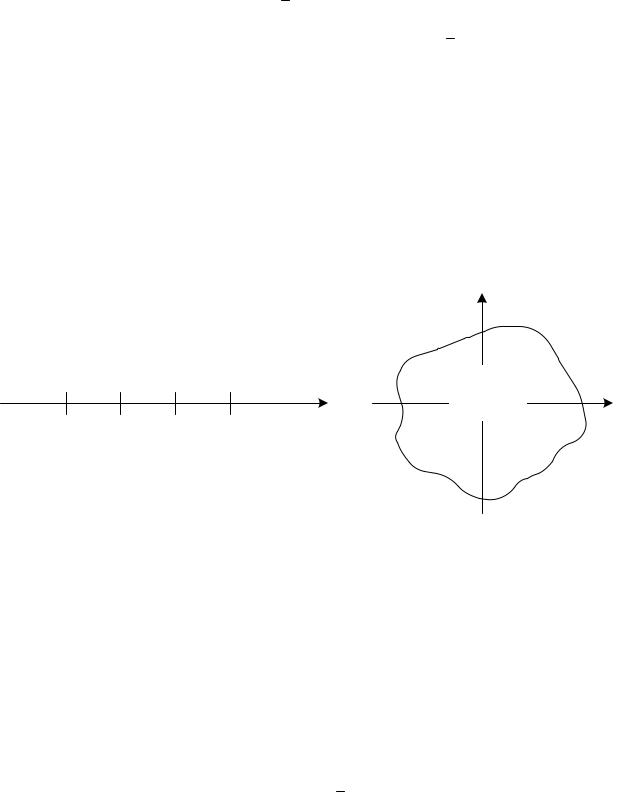
Так, например, если производится только одно наблюдение y1 на отрезке

[a, b], то для конкретного значения y1 должно быть принято либо решение H0 ,

либо H1 . Таким образом, множество G{y1 : a ≤ y1 ≤ b} всех точек отрезка (всех возможных исходов эксперимента) разбивается на две области G0 и G1

(рис.3.1,а).

Если y1 G0 , то принимается решение о справедливости гипотезы H0 ; ес-

ли же y1 G1 , то предпочтение отдается гипотезе H1 . Когда производится два наблюдения y1 , y2 , множество всех исходов эксперимента представляется точ-

ками плоскости G (рис.3.1,б). Поскольку каждому исходу (y1, y2 ) соответствует конкретное решение H0 или H1 , то все множество G так же, как и в одномер-

ном случае, должно быть разделено на два подмножества G0 и G1 (рис.3.1,б).

Очевидно, в общем случае выборки y = (y1, y2 ,..., yn )T произвольного объе-

ма n -мерная область G всех возможных исходов опытов разбивается на две подобласти G0 и G1 . Область G0 , где принимается гипотеза H0 , называют до-

пустимой областью. Вторую область G1 , отклонения гипотезы H0 , называют

108

критической.

Таким образом, построение оптимального правила проверки гипотезы H0

может трактоваться как нахождение наилучшего разбиения пространства G всех возможных результатов эксперимента на две области G0 и G1 или, что в данном случае то же самое, как выбор наилучшей допустимой области.

Для того чтобы выяснить, что следует понимать под наилучшим разбиением, необходимо ввести критерий качества правила принятия решения. Поскольку состояние объекта заранее не известно, а прием сигналов затруднен помехами, то при использовании любого правила решения возможны ошибки. С этой точки зрения после принятия решения возможны четыре ситуации, схематично изображенные на рис.3.2.

Две из них соответствуют правильным решениям (сплошные линии) и две

– ошибочным (пунктир). Ошибка, в результате которой принимается решение H1 при нахождении объекта в состоянии S0 , называется ошибкой первого рода.

Другая ошибка – ошибкой второго рода.

В задачах обнаружения цели состояние S0 и гипотеза H0 соответствуют отсутствию цели, и ошибка первого рода обычно называется ложной тревогой. Ошибка второго рода состоит в принятии неверного решения об отсутствии цели, когда цель присутствует, и называется пропуском цели.

Используя формулу (1.45), нетрудно записать следующие выражения для вероятности ошибки 1 рода [6]:

109

и вероятности ошибки 2 рода:

где d y = dy1 dy2 ... dyn .

Вместо pM можно использовать вероятность противоположного события,

т.е. вероятность правильного решения. Очевидно:

Для заданного размера выборки невозможно одновременно сделать сколь угодно малыми вероятности ошибок первого и второго рода. Например, чтобы уменьшить вероятность ложной тревоги pF , следует уменьшить размер крити-

ческой области G1 , но тогда увеличивается размер допустимой области G0 и

возрастает вероятность ошибки второго рода (3.2). Поэтому «разумный» критерий оптимальности должен быть построен на основе какого-либо компромисса между вкладом двух типов возможных ошибок в общую характеристику или общие показатели системы обнаружения.

Одним из возможных способов построения критерия оптимальности может быть байесовский подход, общая методология которого рассматривалась в предыдущем разделе применительно к задачам оценивания параметров. Точно так же основой байесовского подхода к проблемам обнаружения является введение функции потерь, которая приписывает каждой из четырех возможных ситуаций (рис.3.2) определенную плату. При этом обычно правильным решениям соответствует нулевой размер штрафа. Ошибке первого рода поставим в соответствие плату R0 , а ошибке второго рода – плату размером R1 . Тогда средние потери составят величину

110