
Корольов / Теория связи
.pdf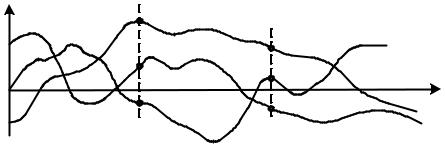
(X1 (ω), X 2 (ω)) называется двумерной СB или системой двух СВ и обозначается
(X1 , X 2 ). Например, если случайный сигнал X (t) на выходе радиоприемного устройства наблюдается в два момента времени t1 и t2 , то упорядоченная пара возможных значений сигнала X1 = X (t1 ) и X2 = X (t2 ) представляет собой двумерную CB (X1, X2 ).
Двумерную СB (X1 , X 2 ) можно рассматривать как случайную точку или как случайный вектор на координатной плоскости. При этом каждому конкретному исходу опыта (x1 , x2 ) ставится в соответствие точка плоскости с координатами x1 и x2 .
1.7.1. Характеристики случайного процесса
Помехи в системах связи описываются методами теории случайных процессов.
Функция называется случайной, если в результате эксперимента она принимает тот или иной вид, заранее неизвестно, какой именно. Случайным процессом называется случайная функция времени. Конкретный вид, который принимает случайный процесс в результате эксперимента, называется реализацией случайного процесса.
x |
xk(t1) |
xk(t2) |
x1(t) |
|
x2(t1) |
||
|
|
||
|
t |
x1(t2) |
xk(t) |
|
1 |
t2 |
t |
|
|
||
|
x1(t1) |
x2(t2) |
x2(t) |
Рис. 1.19. Реализация случайного процесса X(t)
На рис. 1.19 показана совокупность нескольких (трех) реализаций случайного процесса x(1) (t) , x(2) (t) , x(3) (t) . Такая совокупность называется ансамб-
лем реализаций. При фиксированном значении момента времени t = t1 в первом
51

эксперименте получим конкретное значение x(1) (t ) , во втором – |
x(2) (t ) , в треть- |
1 |
1 |
ем – x(3) (t1) .
Случайный процесс носит двойственный характер. С одной стороны, в каждом конкретном эксперименте он представлен своей реализацией – неслучайной функцией времени. С другой стороны, случайный процесс описывается совокупностью случайных величин.
Действительно, рассмотрим случайный процесс X (t) в фиксированный момент времени t = t1 Тогда X (t1) в каждом эксперименте принимает одно зна-
чение x(t1) , причем заранее неизвестно, какое именно. Таким образом, случай-
ный процесс, рассматриваемый в фиксированный момент времени t = t1 являет-
ся случайной величиной. Если зафиксированы два момента времени t1 и t2 , то в каждом эксперименте будем получать два значения x(t1) и x(t2 ) . При этом со-
вместное рассмотрение этих значений приводит к системе ( X (t1), X (t2 )) двух случайных величин. При анализе случайных процессов в N моментов времени приходим к совокупности или системе N случайных величин ( X (t1),..., X (tN )) .
Математическое ожидание, дисперсия и корреляционная функция случайного процесса. Поскольку случайный процесс, рассматриваемый в фиксированный момент времени, является случайной величиной, то можно говорить о математическом ожидании и дисперсии случайного процесса:
m(t) = M {X (t)}, D(t) = M {X (t) − m(t))2 }.
Так же, как и для случайной величины, дисперсия характеризует разброс значений случайного процесса относительно среднего значения m(t) . Чем больше D(t) , тем больше вероятность появления очень больших положитель-
ных и отрицательных значений процесса. Более удобной характеристикой явля-
ется среднее квадратичное отклонение (СКО) σ(t) = D(t) , имеющее ту же раз-
мерность, что и сам случайный процесс.
Если случайный процесс описывает, например, изменение дальности до объекта, то математическое ожидание – средняя дальность в метрах; дисперсия
52
измеряется в квадратных метрах, а СКО – в метрах и характеризует разброс возможных значений дальности относительно средней.
Среднее значение и дисперсия являются очень важными характеристиками, позволяющими судить о поведении случайного процесса в фиксированный момент времени. Однако, если необходимо оценить «скорость» изменения процесса, то наблюдений в один момент времени недостаточно. Для этого используют две случайные величины ( X (t1), X (t2 )) , рассматриваемые совместно.
Так же, как и для случайных величин, вводится характеристика связи или зависимости между X (t1) и X (t2 ) . Для случайного процесса эта характеристика зави-
сит от двух моментов времени t1 и t2 и называется корреляционной функцией:
R(t1,t2 ) = M {( X (t1) − m(t1)(X (t2 ) − m(t2 ))}.
Стационарные случайные процессы. Многие процессы в системах управления протекают однородно во времени. Их основные характеристики не изменяются. Такие процессы называются стационарными. Точное определение можно дать следующим образом. Случайный процесс X (t) называется стацио-
нарным, если любые его вероятностные характеристики не зависят от сдвига начала отсчета времени. Для стационарного случайного процесса математическое ожидание, дисперсия и СКО постоянны: m(t) = m , D(t) = D =σ 2 .
Корреляционная функция стационарного процесса не зависит от начала отсчета t, т.е. зависит только от разности τ = t2 −t1 моментов времени:
R(τ) = M {( X (t1) − m) ( X (t1 −τ) − m)}.
Корреляционная функция стационарного случайного процесса имеет следующие свойства:
1) R(τ = 0) = σ 2 ; 2) R(τ) = R(−τ) ; 3) R(τ → ∞) = 0 .
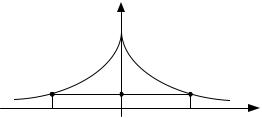
Часто корреляционные функции процессов в системах связи имеют вид, показанный на рис. 1.20.
53
R(τ)
σ 2
σ 2 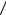 е
е
0 |
τk |
τ |
Рис. 1.20. Корреляционные функции процессов
Интервал времени τk , на котором корреляционная функция, т.е. величина связи между значениями случайного процесса, уменьшается в М раз, называется интервалом или временем корреляции случайного процесса. Обычно M =10 или M = e . Можно сказать, что значения случайного процесса, отличающиеся по времени на интервал корреляции, слабо связаны друг с другом.
Таким образом, знание корреляционной функции позволяет судить о скорости изменения случайного процесса.
Другой важной характеристикой является энергетический спектр случайного процесса. Он определяется как преобразование Фурье от корреляционной функции:
G(ω) = ∞∫R(τ)e− jωτ dτ .
−∞
Очевидно, справедливо и обратное преобразование:
R(τ) = |
1 |
∞∫G(ω)e jωτ dω . |
|
||
|
2π −∞ |
|
Энергетический спектр показывает распределение мощности случайного процесса, например помехи, на оси частот.
При анализе САУ очень важно определить характеристики случайного процесса на выходе линейной системы при известных характеристиках процесса на входе САУ. Предположим, что линейная система задана импульсной переходной характеристикой h(τ ). Тогда выходной сигнал в момент времени t1
определяется интегралом Дюамеля:
x(t1 )= ∞∫h(τ1 )g(t1 −τ1 )dτ1 ,
−∞
54
где g(t) – процесс на входе системы. Для нахождения корреляционной функции
Rx (t1 ,t2 )= M {x(t1 )x(t2 )} запишем x(t2 )= ∞∫h(t2 )g(t2 −τ2 )dτ2 и после перемножения най-
−∞
дем математическое ожидание
Rx (t1,t2 )= ∞∫ ∞∫h(τ1 )h(τ2 )M {g(t1 −τ1 )g(t2 −τ2 )}dτ1dτ2 .
−∞ −∞
Таким образом, связь между корреляционными функциями входного и выходного случайных процессов устанавливается с помощью следующего двойного интеграла:
Rx (t1,t2 )= ∞∫ ∞∫h(τ1 )h(τ2 )Rg (t1 −τ1,t2 −τ2 )dτ1dτ2 .
−∞ −∞
Для стационарных процессов корреляционные функции зависят только от разности аргументов t1 −t2 = u , (t1 −τ1 )−(t2 −τ2 )= v и поэтому
Rx (u)= ∞∫ ∞∫h(τ1 )h(τ2 )Rg (v)dτ1dτ2 .
−∞ −∞
Более простое соотношение можно найти для энергетических спектров Gg (ω) и Gx (ω) входного и выходного сигналов при известной передаточной функции W (jω) линейной системы. Действительно, найдем преобразование Фу-
рье от левой и правой частей последнего равенства. Получим следующее выражение:
Gx (ω) = ∞∫ ∞∫ ∞∫h(τ1) h(τ2 ) Rg (ν)e− jω udτ1 dτ2 du .
|
−∞ −∞ −∞ |
|
|
|
|
|
|
|
|
||
После замены переменной v = t1 −t2 − (τ1 −τ2 )= u −τ1 −τ2 |
или u = v +τ1 −τ2 тройной |
||||||||||
интеграл преобразуется в произведение |
|
|
|
|
|
|
|
||||
|
Rx (u)= ∞∫ ∞∫h(τ1 )h(τ2 )Rg (v)dτ1dτ2 |
|
|
|
|||||||
|
|
|
−∞ −∞ |
|
|
|
|
|
|
|
|
|
∞ |
− jωτ1 |
∞ |
jωτ2 |
|
∞ |
|
jων |
|
||
|
∫h(τ1 )e |
|
∫h(τ2 )e |
dτ2 |
|
∫Rg (ν)e |
|
||||
Gx (ω) = |
|
dτ1 |
|
|
|
dν . |
|||||
|
−∞ |
|
|
−∞ |
|
|
|
−∞ |
|
|
|
55

Поскольку преобразование Фурье от импульсной характеристики дает передаточную функцию, находим окончательно связь между энергетическими спектрами процессов на входе и на выходе линейной системы:
Gx (ω)=W (jω)W (− jω)Gg (ω) = W (jω)2 Gg (ω) .
Часто помехи в системах управления имеют очень широкий спектр. В таких случаях их удобно представить в виде так называемого белого шума – процесса с постоянным энергетическим спектром: G(ω) = N0 . Корреляционная функция белого шума R(τ) = N0δ(τ) , где δ(t) – импульсная дельта-функция. Это означает, что даже очень близкие по времени значения белого шума не связаны друг с другом.
1.7.2. Флуктуационный шум
Примером случайного процесса является флуктуационный шум, наиболее характерный для большинства каналов электросвязи. Для количественных расчетов воздействия флуктуационного шума на сигнал необходимо знать основные вероятностные характеристики. Поскольку шум образуется как сумма большого числа отдельных независимых колебаний, он, согласно центральной предельной теореме представляет собой стационарный эргодический случайный процесс с гауссовским (нормальным) распределением вероятности.
ПРВ гауссовского процесса описывается формулой [6, 32]:
w(x)= |
1 |
|
(x −m)2 |
, |
(1.47) |
||
|
exp − |
|
|
|
|||
2πσ |
2σ |
2 |
|||||
|
|
|
|
|
|
||
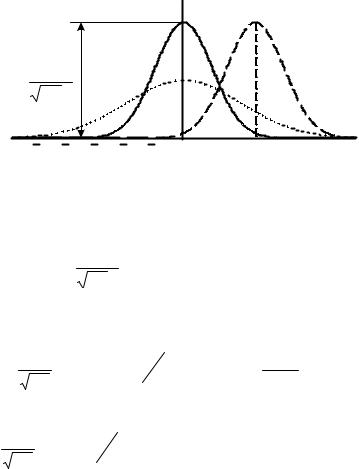
в которую входят два числовых параметра m и σ2 , имеющие смысл математического ожидания и дисперсии: σ 2 = D(X ). График плотности вероятности w(x) представляет собой колоколообразную кривую с единственным максимумом в точке x = m (рис. 1.21). Из графика видно, что с уменьшением σ кривая все более локализуется в окрестности точки x = m . Для флуктуационного шума обычно
56
|
|
|
|
w σ1 =1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
σ1 =1 |
|
|
1 |
|
|
|
|
|
|
σ2 = 2 |
|
|
|
|
2πσ |
|
|
|
|
|
|
|
|
|
||
5 |
4 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
x |
Рис. 1.21. Гауссовское распределение вероятностей: |
|||||||||||
Функция распределения вероятности для гауссовского случайного процесса:
|
|
F(x)= |
1 |
|
|
x |
|
|
(x −m)2 |
|
|
|
|
|
||||
|
|
|
|
|
∫exp − |
|
|
dx . |
|
|
|
|
||||||
|
|
πσ |
|
|
2σ 2 |
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
После замены переменных y = |
|
(x − m) |
эта функция приводится к виду: |
|
||||||||||||||
|
|
σ |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F(x)= |
1 |
|
( x−m) /σ |
|
− y |
2 |
|
|
+Ф |
x −m |
, |
|
||||||
|
|
∫ |
exp |
|
|
dy = 0,5 |
|
|
|
(1.48) |
||||||||
|
|
2π |
|
|
2 |
|
|
|
o |
|
σ |
|
|
|||||
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фo (z)= |
1 |
x |
|
|
|
|
|
- интеграл вероятности. |
|
|||||||||
∫ |
|
|
|
|
||||||||||||||
|
exp − y2 |
|
dy |
|
||||||||||||||
|
2π |
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
Функция Ф0 (z) табулирована в математических справочниках. Заметим, что Ф0 (− z)= −Ф0 (z), Ф0 (0)= 0 , Ф0 (∞)= 0,5 . Для приближенных вычислений можно воспользоваться приближенным выражением:
Фo (z)≈ 0,5 −0,65exp[−0,44(z +0,75)2 ] |
(1.49) |
Пример 1.3. Вычислим вероятность того, что мгновенное значение флук- |
|
туационного шума с нулевым средним и дисперсией σ 2 = 9[B2 ] |
превысит уро- |
вень x0 = 6[B]. |
|
Исходя из определения функции распределения вероятности (1.43), вероятность превышения случайным процессом уровня x0
p(X > xo )=1− p(X ≤ xo )=1− F(xo ).
Подставляя значение F(x0 ) для гауссовского случайного процесса, полу-
чаем:
p(X > xo )=1−0,5 −Фo [(xo −m)/σ]= 0,5 −Фo [(xo −m)/σ].
Для заданных числовых значений и m = 0 , воспользовавшись таблицами или приближенной формулой (1.49) для Φ0 (z), получаем:
p(X > 6)≈ 2,33 10−2 .
Спектральная плотность мощности Gx (f ) флуктуационного шума зависит
57

от физической природы его образования, а также участка канала связи, где он рассматривается. Обычно спектральная плотность мощности Gx (f ) флуктуационного шума постоянна в широком диапазоне частот, т. е. можно приближенно считать, что: G( f ) = No при 0 ≤ f ≤ ∞ . В этом случае шум называют белым. Это название дано по аналогии с белым светом, имеющим все частотные компоненты.
1.8. Комплексное представление сигналов и помех
Ранее было изучено представление детерминированных сигналов рядами ортогональных функций. Такая модель оказывается особенно полезной при анализе прохождения сигналов через линейные радиотехнический устройства.
Вместе с тем при анализе нелинейных преобразований сигналов и, в частности, модуляции и демодуляции, требуется иной подход. Этот подход основывается на понятии аналитического сигнала.
1.8.1. Понятие аналитического сигнала
Многие формулы гармонического анализа записываются значительно проще и некоторые задачи решаются легче, если использовать в качестве элементарных функций не обычные действительные синусоиды, а экспоненциальные функции мнимого аргумента. Действительно, по формуле Эйлера [6, 21]:
|
cos(ωt +ϕ)= |
1 |
[exp{j(ωt +ϕ)}+exp{− j(ωt +ϕ)}]. |
|
(1.50) |
||||
|
|
||||||||
|
|
2 |
|
|
|
|
|
|
|
|
Этой записи можно дать геометрическую трактовку, пользуясь представ- |
||||||||
лением комплексных чисел в виде точек или векторов на плоскости. |
|
|
|
|
|||||
|
Выражение exp j(ωt +ϕ) представляет в данном случае вектор единичной |
||||||||
|
|
|
|
|
длины, проведенный под углом ωt +ϕ к дейст- |
||||
|
Im |
ω |
|
вительной оси (рис.1.22). При изменении вре- |
|||||
|
|
||||||||
|
|
1 |
|
|
мени t этот вектор, единичной длины, |
меняет |
|||
|
|
|
|
|
положение, вращаясь в положительном на- |
||||
|
|
ωt + ϕ |
|
правлении с угловой скоростью ω. |
|
|
|
|
|
|
|
|
Изобразить синусоиду в форме (1.50), это |
||||||
|
|
|
Re |
значит представить ее суммой двух векторов, |
|||||
|
|
|
|
|
|||||
|
|
|
|
|
длина каждого из которых равна |
1 |
2 |
, |
распо- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ложенных в любой момент времени симмет- |
||||
|
|
|
|
|
рично относительно действительной оси и |
||||
вращающихся |
в разных |
направлениях с угловыми скоростями |
ω |
|
и −ω |
||||
(рис.1.23). |
|
|
|
|
|
|
|
|
|
58
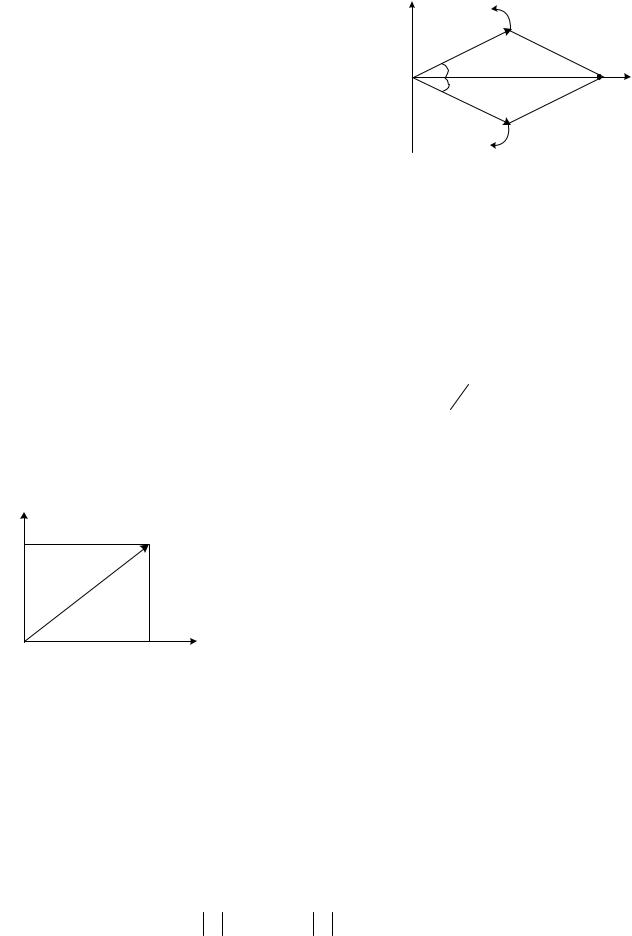
В момент t = 0 они занимают положения |
|
|
ω |
|
||
под углами ϕ и −ϕ относительно действи- |
Im |
|
|
|||
|
|
|
||||
тельной оси. Геометрическая сумма векторов |
|
|
|
|
||
всегда совпадает по направлению с действи- |
|
|
|
|
||
тельной осью и представляет действительную |
|
|
|
Re |
||
функцию времени cos(ωt +ϕ). |
|
|
− ω |
|
||
При представлении косинусоиды в виде |
|
|
|
|||
|
|
|
|
|||
cos(ωt +ϕ)= Re[exp j(ωt +ϕ)] |
можно ограничиться |
|
|
|
|
|
одним вращающимся в положительном на- |
|
|
|
|
||
правлении вектором и представить косинусоиду его проекцией на действитель- |
||||||
ную ось. |
|
|
|
|
|
|
В этом случае нет необходимости вводить отрицательные частоты. Длина |
||||||
вектора представляет амплитуду косинусоиды, а угол, образуемый им в данный |
||||||
момент с действительной осью, - полную фазу (ωt +ϕ). |
|
|
|
|||
Проекция этого вектора на мнимую ось равна Im[exp j(ωt +ϕ)]= sin(ωt +ϕ), т.е. |
||||||
представляет ту же косинусоиду, сдвинутую по фазе на π |
2 |
(рис. 1.24). |
|
|||
|
|
|
|
|
||
Многие сигналы в системах электросвязи можно представлять в виде: |
||||||
S(t)= A(t)cos[ω t +ϕ(t)], |
|
|
(1.51) |
|||
т.е. как «квазигармоническую» функцию с переменными «амплитудой» и «на- |
||||||
Im |
чальной фазой». Такой |
сигнал можно интерпрети- |
||||
ровать геометрически |
как проекцию на действи- |
|||||
1 |
||||||
sin(ωt + ϕ ) |
тельную ось вращающегося вектора, но при |
этом |
||||
|
изменяющего свою длину и угловую скорость. Для |
|||||
Re |
описания свойств сигнала представленного в форме |
|||||
(1.51) вводят понятие комплексного аналитического |
||||||
cos(ωt + ϕ ) |
||||||
сигнала. |
|
|
|
|
||
|
Рассмотрим отрезок сигнала на некотором |
|||||
|
интервале времени 0 < t < T . |
|
|
|
||
Его можно представить на этом интервале рядом Фурье в экспоненциаль- |
||||||
ной форме [6, 21]: |
|
|
|
|
|
|
∞ |
|
2π |
|
|
|
S(t)= ∑Sk e jkωot ,ω0 |
= |
. |
(1.52) |
||
|
|||||
−∞ |
|
T |
|
||
Пользуясь геометрическим представлением синусоиды, можно предста- |
|||||
вить сигнал S(t) в виде суммы вращающихся векторов, |
каждый из которых |
||||
имеет вид:
Sk e jkωot = Sk e jϕk e jkωot = Sk e j(kωot +ϕk ) .
59
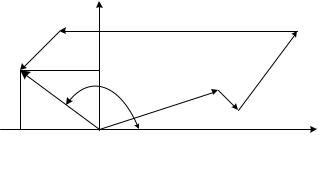
Векторы с индексами k > 0 вращаются в положительном направлении, а с |
|||||||
k < 0 в отрицательном. Пара таких векторов с индексами k |
и − k образует одну |
||||||
действительную косинусоиду. |
|
|
|
|
|||
Поэтому предполагая среднее состояние сигнала нулевым ( S0 = 0 )косину- |
|||||||
соида может быть представлена проекцией на действительную ось одного век- |
|||||||
тора, вращающегося, например, в положительном направлении. Вместо (1.68) |
|||||||
можно взять проекцию (т.е. действительную часть) суммы векторов, вращаю- |
|||||||
щихся только в положительном направлении, увеличив их величину вдвое: |
|||||||
|
|
S(t) |
∞ |
|
|
|
|
|
|
= Re ∑2Sk |
e jkωot ,0 < t <T . |
(1.53) |
|||
|
|
|
k =1 |
|
|
|
|
Ряд в правой части (1.53) представляет собой комплексную функцию |
|||||||
времени, которую обозначим S(t) |
и будем называть комплексным или аналити- |
||||||
ческим сигналом: |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
S(t)= ∑2Sk |
e jkωot ,0 < t <T . |
(1.54) |
|||
|
|
|
k =1 |
|
|
|
|
Его геометрическим представлением является вектор, образующийся при |
|||||||
суммировании элементарных векторов Sk ,k =1,2,... . Так как элементарные век- |
|||||||
|
|
|
|
|
|
торы вращаются с разными угловы- |
|
Im |
2S4 |
|
|
ми скоростями |
kω0 , то их взаимная |
||
2S5 |
|
|
|
конфигурация со временем изменя- |
|||
|
|
|
|
|
|||
|
|
|
|
|
ется. Поэтому их векторная сумма |
||
~ |
(t ) |
|
|
|
2S3 |
||
S |
|
2S2 |
|
(рис. 1.25) представляет собой век- |
|||
S(t) |
ϕ(t) |
|
|
||||
|
2S |
|
|
Re |
тор с переменной длиной, вращаю- |
||
|
|
1 |
|
|
|
щийся с переменной угловой скоро- |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
стью. |
|
|
|
|
|
|
|
Исходный сигнал (1.51) явля- |
|
ется действительной частью аналитического сигнала. |
|
||||||
Учитывая выражение (1.19) для комплексных коэффициентов ряда Фурье |
|||||||
получим: |
|
|
|
|
|
|
|
|
|
S(t)= Re S(t)= ∑∞ |
Re[(ak − jbk )e jkω0t ]= |
|
|||
|
|
|
k =1 |
|
|
|
(1.55) |
|
|
∞ |
|
|
|
|
|
|
|
= ∑(ak cos kω0t +bk sin kω0t),0 < t <T, |
|
||||
|
|
k =1 |
|
|
|
|
|
что является обычным разложением сигнала в ряд Фурье в тригонометрической форме.
Мнимая часть аналитического сигнала представляет собой некоторую функцию времени, однозначно определяемую исходным сигналом S(t).
60
