
Корольов / Теория связи
.pdf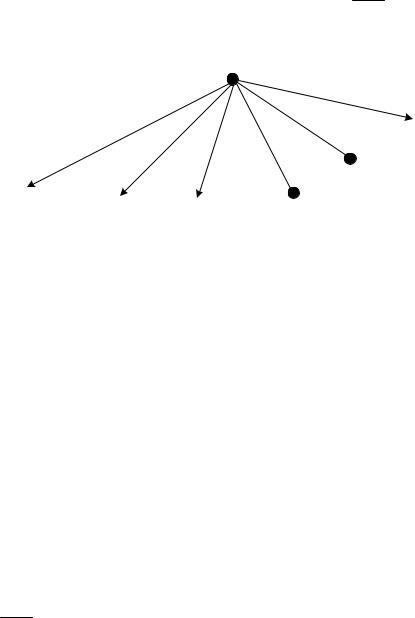
Полученный результат имеет ясную геометрическую трактовку. Действительно, di2 (YT , Si ) является расстоянием между функциями YT = (y(t),t (0,T )) и
Si (t),t (0,T ) в гильбертовом пространстве со среднеквадратической метрикой. С
этой точки зрения оптимальное решение по наблюдениям YT заключается в вы-
боре такого из возможных переданных сигналов Si (t),i =1, M x , который находится ближе других к YT . Рис 5.13 иллюстрирует оптимальный выбор S2 .
|
|
|
ρM x |
|
ρ1 |
|
SM x |
|
ρ2 |
ρ |
|
S1 |
|
3 |
|
S2 |
S3 |
|
|
|
|
||
Рис. 5.13. Геометрическая интерпретация приема сигналов |
|||
Преобразуем теперь (5.44) к следующему виду: |
|||
|
di2 (YT , Si )= T∫y2 (t)dt −2T∫y(t)Si (t)dt +T∫Si2 (t)dt . |
||
|
0 |
0 |
0 |
Первый интеграл не зависит от i , |
а при равных энергиях сигналов |
||
T∫Si2 (t)dt минимум di2 достигается при максимальном значении корреляционного
0
интеграла:
λi = T∫y(t)Si (t)dt,i = |
|
. |
(5.45) |
1, M x |
|||
0 |
|
|
|
Структурная схема приемника (рис. 5.14), использующего вычисления по формуле (5.45), включает набор корреляторов и блок выбора наибольшего из чисел λi ,i =1, M x .
На выходе приемника вырабатывается наилучшая с точки зрения минимума вероятности ошибки оценка x€j переданного сообщения по принятой реализации Yt . Рассмотренную процедуру называют приемом сигналов в це-
лом.
271

|
|
|
|
λ1 |
|
|
|
|
|
|
|
|
|
|
|
y(t ) |
|
|
|
λ2 |
|
|
xˆ j |
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
λi |
|
λ |
||
|
|||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
λM x |
|||
|
|
|
|
|
|
|
|
|
|
|
M x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При переходе к кодам значительной длины число используемых в системе сигналов и соответствующее число корреляторов растет очень быстро (M x = 2k ), и сложность всего устройства может оказаться неприемлемо большой.
Существенного упрощения можно достичь, используя посимвольный прием сигналов, то есть разбивая процедуру приема на две части:
оптимальный прием каждого символа и принятие решения о его значе-
нии;
декодирование полученных кодовых слов. В этом случае структура приемника наиболее проста (рис. 5.15).
|
|
|
t1 +τ |
|
|
|
|
|
|
|
|
|
|
|
∫ yS0dt |
|
|
λ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t ) |
|
|
|
|
|
|
|
0,1 |
|
|
xˆ j |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Схема |
|
Декодер |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
сравнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 +τ |
|
|
|
|
|
|||
|
|
|
∫ |
yS1dt |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
t1 |
|
|
|
|
|
|
|
|
Рис. 5.15. Посимвольный прием
Для бинарного канала связи приемник содержит два коррелятора, схему сравнения и декодер. На выходе схемы сравнения появляется сигнал «0», если λ0 > λ1 , или сигнал «1», если λ0 ≤ λ1 . Возможно и дальнейшее упрощение схемы за счет объединения двух корреляторов в один, используя в качестве опорного
272

сигнала разность S0 (t)− S1 (t).
Платой за существенное снижение сложности алгоритма при переходе от оптимального к посимвольному приему является увеличение вероятности ошибки. Поэтому нашей очередной задачей будет анализ характеристик рассмотренных алгоритмов и их сравнение при различных видах кодов.
5.9.2. Помехоустойчивость систем передачи информации при оптимальной процедуре приема
Пусть по каналу связи передается сигнал Si (t). Очевидно, прием будет правильным, когда выходной сигнал λi коррелятора (рис. 5.14) окажется наи-
большим. Поэтому вероятность правильного приема сигнала может
быть найдена как вероятность совместного выполнения системы неравенств
λi > λj ;i, j =1, M x ,i ≠ j . При фиксированном значении λi легко находится условная вероятность выполнения этой системы неравенств:
pПРi (λi )= λ∫i ...λ∫i w(λ1 ,...,λM x  λi )dλ1...dλi−1dλi+1...dλM x ,
λi )dλ1...dλi−1dλi+1...dλM x ,
−∞ −∞
где w(λ1,...,λM x  λi ) – условная плотность распределения λ1...λi−1λi+1...λM x при фик-
λi ) – условная плотность распределения λ1...λi−1λi+1...λM x при фик-
сированном λi .
Безусловная вероятность правильного приема сигналов в системе находится с помощью усреднения pПРi (λi ) по λi и i :
M |
+∞ λi |
λi |
)dλ1dλ2 ...dλM x . |
|
pПР = ∑x |
p(Si )∫ ∫... ∫w(λ1 ,...,λM x |
(5.46) |
||
i=1 |
−∞−∞ |
−∞ |
|
|
В общем случае интегрирование (5.46) является сложной математической задачей. Поэтому ограничимся рассмотрением частного случая ортогональных сигналов, а также близких к ним симплексных сигналов, для которых величины λi и λj , j ≠ i независимы. В этом случае совместная плотность распределения может быть записана в виде произведения:
w(λ1 ,...,λM x )= ∏M x w(λj ).
j=1
273
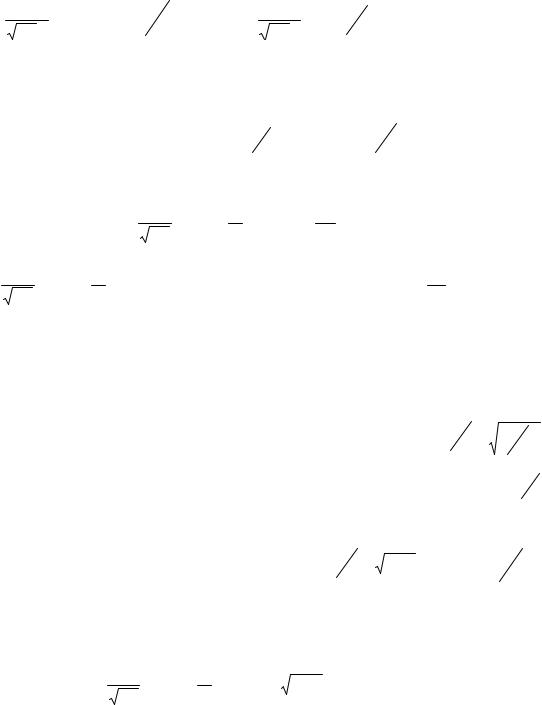
Вследствие свойства эквидистантности ортогональных кодов вероятности pПРi равны между собой, следовательно,
|
|
|
|
|
|
+∞ |
+∞ |
|
|
|
M x −1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
∫w(λ)dλ |
|
dλi , |
|
|
||||
|
|
|
|
pПРi (λi )= ∫w(λi ) |
|
|
|
||||||||||
|
|
|
|
|
|
−∞ |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
w(λi )= |
1 |
|
2 |
|
|
|
w(λ)= |
|
|
1 |
|
exp[−λ |
2 |
2 ]; |
|
|
где |
2πσ |
exp −(λi −Uc ) |
2σ |
2 |
; |
|
2πσ |
2σ |
Uc – сигнальная |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
составляющая на выходе i -го коррелятора; |
|
σ2 |
|
– дисперсия шумовой состав- |
|||||||||||||
ляющей на выходах корреляторов. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Переходя к новым переменным t1 = λ |
σ |
и |
t1 = (λi |
−Uc ) |
, преобразуем вы- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
||
ражение для вероятности ошибки к виду:
где |
Φ(z)= |
1 |
+∞ |
|
|
|
|
− |
|||
2π |
∫exp |
||||
|
|
−∞ |
|
|
|
pПР =
2 |
|
t1 |
|
2 |
dt1 |
|
1 |
+∞ |
|
|
t |
2 |
|
M x −1 |
|
Uc |
|
|
|
− |
|
|
||||||
2π |
∫exp |
2 |
Φ |
|
t + |
σ |
dt . |
|||
−∞ |
|
|
|
|
|
|
||||
– интеграл вероятности. Величина Uσc (отношение
сигнал/шум) может быть найдена следующим образом. При действии белого шума выходной сигнал коррелятора совпадает с выходным сигналом согласованного фильтра. Следовательно, можно воспользоваться известной формулой
для отношения сигнал/шум на выходе согласованного фильтра: |
Uc |
σ |
= |
2E |
N0 |
, |
||
|
|
|
|
|
|
|||
где E – энергия сигнала. В теории связи обычно вводится параметр E0 |
= E |
k |
, |
|||||
|
|
|
|
|
|
|
|
|
характеризующий энергию сигнала на один бит передаваемой информации при
числе информационных символов k . Окончательно Uc σ = 2h0 k , где h0 |
= E0 N0 |
– |
|||||||||
параметр, принятый в системах связи. |
|
|
|
|
|
||||||
Выражение для вероятности правильного приема сигнала |
|
|
|||||||||
|
1 |
+∞ |
|
|
t |
2 |
|
M x −1 |
(t + 2h0 k )dt . |
|
|
pПР = |
|
|
− |
|
|
(5.47) |
|
||||
|
∫exp |
2 |
Φ |
|
|
||||||
|
2π −∞ |
|
|
|
|
|
|
|
|||
часто называется интегралом В.А. Котельникова. Можно показать, что для симплексных сигналов справедливо следующее выражение:
274

|
1 |
+∞ |
|
|
t |
2 |
|
M x −1 |
(t + 2h0 k(1 |
− ρ))dt . |
|
pПР = |
|
|
|
|
|
(5.48) |
|||||
π |
∫exp |
− |
2 |
Φ |
|
||||||
|
2 |
−∞ |
|
|
|
|
|
|
|
|
|
где ρ – коэффициент корреляции сигналов Si (t) и S j (t), j ≠ i .
Сравнение помехоустойчивости систем передачи информации, использующих разные коды, по величине pПР не всегда удобно, так как коды могут иметь разное число k информационных символов. С изменением k меняется как pПР , так и количество передаваемой информации. Поэтому вероятность пра-
вильного приема приводится к одному биту передаваемой информации, для чего вводят новую характеристику QЭ , равную эквивалентной вероятности иска-
жения одного бита информации. Реальный канал связи заменяется эквивалент-
ным каналом без избыточности, |
но так, чтобы вероятности pПР были одина- |
|
ковы в обоих каналах. В системе без избыточности |
pПР = (1−QЭ )k поэтому |
|
QЭ = k |
pПР ≈ 1− pПР . |
(5.49) |
|
k |
|
Для анализа помехоустойчивости при разных значениях параметра h0 ,
имеющего смысл приведенного отношения сигнал/шум, по формулам (5.47), (5.48) можно вычислить вероятности pПР и найти QЭ с помощью (5.49).
На рис. 5.16 сплошными кривыми представлены результаты таких расчетов для случаев k = n (безызбыточное кодирование), а также симплексных кодов (7,3), (15,4), (1023,10). Как следует из рисунка, с ростом числа k информационных разрядов вероятность QЭ ошибки монотонно падает.
Представляет интерес предел QЭ при k → ∞ , что соответствует переходу ко все более сложным кодам. Для его определения заметим, что функция Φ(z)M x −1
при увеличении k = log2 M x приближается по форме к единичному скачку в неко-
торой точке z0 , значение которой определяется из уравнения Φ(z)M x −1 = 0,5 и рав-
но z0 ≈  2k ln 2 . При k → ∞ формула (5.47) приводится к виду:
2k ln 2 . При k → ∞ формула (5.47) приводится к виду:
|
|
|
1 |
|
+∞ |
|
|
|
t |
2 |
|
|
1, h > ln 2, |
|
|
|
|
|
|
|
|||||||
p |
|
= lim |
|
∫ |
exp |
|
− |
|
|
|
0 |
||
ПР |
|
|
|
|
|
dt = |
|
|
|||||
|
k →∞ |
2π |
|
|
|
2 |
|
|
0, h0 ≤ ln 2. |
||||
|
|
|
z |
− 2h k |
|
|
|
|
|||||
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
Итак, при возрастании числа k |
информационных разрядов в коде величина |
||||||||||||
275
QЭ монотонно падает, если h0 > ln 2 . При достаточно большом k система приобретает пороговый эффект (рис. 5.16, кривая k → ∞ ); при h0 > hпор = ln 2 , QЭ → 0 ;
при h0 ≤ hпор = ln 2 , QЭ → 0,5 .
QЭ |
|
|
|
|
|
10−1 |
|
|
|
|
|
10−2 |
|
|
|
|
|
10−3 |
|
|
|
|
|
10−4 |
|
|
|
|
|
10−5 |
|
|
|
k = n |
|
|
|
|
|
||
10−6 |
|
|
|
|
|
10−7 |
|
|
|
|
|
2 |
4 |
6 |
8 |
10 |
h0 |
В диапазоне h0 > ln 2 возможна передача сообщений со сколь угодно малой вероятностью ошибки. Достигается это только ценою увеличения блока кодируемых информационных символов и соответствующего возрастания времени задержки при кодировании и декодировании, а также сложности оборудования на обеих сторонах системы связи.
5.9.3. Помехоустойчивость систем передачи информации при посимвольном приеме сигналов
Вероятность правильного приема одного символа в этом случае находится
276

с помощью формулы (5.48) при M x = 2 . При использовании для передачи сигна-
лов фазовой манипуляции (ФМн), характеризуемой коэффициентом корреляции между сигналами ρ = −1 ,
|
|
+∞ |
|
|
t |
2 |
|
t + |
4E1 |
N0 |
|
|
2 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
(5.50) |
|||||||||
pПР1ФМ = |
|
|
− |
|
|
∫ |
|
|
− |
ti |
|
|
|
|
||||
2π |
∫exp |
2 |
|
2π |
|
exp |
2 |
dti dt , |
|
|
|
|||||||
|
−∞ |
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|||||
где E1 – энергия одного символа. После замены V = ti +t |
, |
V1 |
= ti −t |
выражения |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
для вероятности правильного ( pПР1ФМ ) и ошибочного ( pФМ ) приема символа при ФМн преобразуются к следующему виду:
p |
|
|
2E |
|
; |
p |
=1 |
|
2E |
|
|
ПР1ФМ |
= Φ |
1 |
|
−Φ |
1 |
. |
(5.51) |
||||
|
|
N0 |
|
|
ФМ |
|
|
N0 |
|
||
|
|
|
|
|
|
|
|
|
|
Аналогично при использовании частотной (ЧМн) или амплитудной (АМн) манипуляций:
p |
|
|
E |
|
; |
p |
=1 |
|
E |
|
|
ПР1ЧМ |
= Φ |
1 |
|
−Φ |
1 |
. |
(5.52) |
||||
|
|
N0 |
|
|
ЧМ |
|
|
N0 |
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
E |
|
; |
|
|
|
E |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
(5.53) |
|
pПР1АМ = Φ |
2N0 |
|
pАМ =1−Φ |
2N |
. |
||||||
|
|
|
|
|
|
|
|
0 |
|
||
По результатам оценки каждого символа декодер выносит решение о всем принятом сигнале. Эффективность работы системы передачи информации целесообразно оценить раздельно для следующих двух вариантов организации системы передачи информации.
Случай заданного канала связи
Пусть параметры двоичного симметричного канала связи (длительность символа τ и вероятность его искажения p ) являются неизменными, а при смене кода (изменении k n ) меняется скорость передачи. Следовательно, такой источ-
ник сообщений должен быть управляемым [10] в отношении своей производительности.
Вероятность правильного принятия решения декодером по всей комбинации символов равна сумме вероятностей появления ошибок, исправляемых де-
277
кодером, включая ошибку нулевой кратности. Для совершенных кодов
qиспр |
|
pПР = ∑Cni pi (1− p)n−i ; |
|
i=0 |
|
для любых других |
|
qиспр |
|
pПР = ∑Cni pi (1− p)n−i +∆p , |
(5.54) |
i=0
где p – вероятность искажения одного символа; ∆p – вероятность исправле-
ния ошибок кратности выше qиспр = d02−1 ; [•] – означает целую часть числа; d0 –
кодовое расстояние. Процедуры исправления ошибок кратности выше qиспр за-
метно усложняют декодер и поэтому реализуются не всегда.
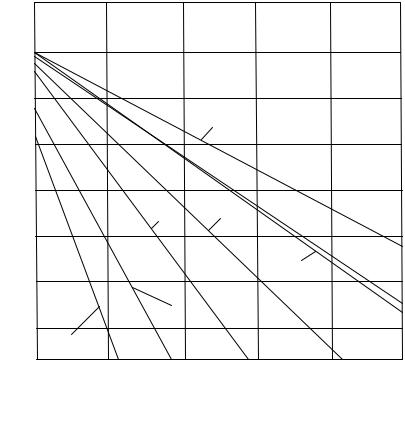
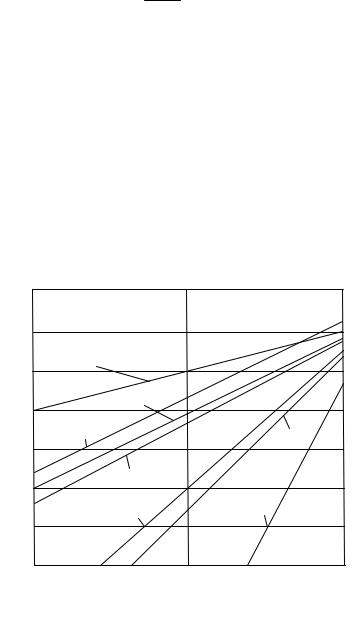
Расчет эффективности системы передачи информации сводится к вычислению pПР , QЭ по формулам (5.49), (5.54) для заданных k , n и d0 . На рис. 5.17
приведены зависимости QЭ от вероятности p искажения одного символа для разных кодов.
QЭ |
|
|
|
10−1 |
|
|
|
|
k = n,QЭ = p |
|
|
10−2 |
|
|
|
10−3 |
|
|
|
10−4 |
|
|
|
10−5 |
|
|
|
10−6 |
|
|
|
10 |
−7 |
10−2 |
10−1 p |
10−3 |
|||
Все коды в этом случае дают заметный выигрыш по сравнению с безызбы-
278
точной передачей. Коды (7,3) и (7,4) близки по эффективности. Остальные коды располагаются в порядке возрастания кодового расстояния и числа избыточных символов.
Модель заданного канала связи хорошо соответствует случаю организации обмена информацией между блоками одного устройства, например, вычислительного комплекса. Из приведенных кривых следует, в частности, что применение кода (15.7) выгоднее трехкратного дублирования семи информационных символов. В этом случае выше и скорость передачи (15 тактов вместо 21), и помехоустойчивость.
Случай заданной производительности источника
Пусть источник сообщений характеризуется производительностью H ′(x).
Применяя для передачи тот или иной код (n, k ), необходимо обеспечивать скорость передачи информации по каналу связи, соответствующую производи-
тельности |
′ |
k |
, где τ |
– длительность одного символа. |
|
||||
H (x)= nτ |
||||
Разные коды имеет разное отношение k n . Следовательно, со сменой кода в общем случае должна меняться длительность символа, а значит, и полоса про-
пускания канала связи, и энергия на один символ E1 = En = En0k , что следует учесть
в формулах (5.51), (5.52), (5.53). Так, при ФМ вероятность ошибочного опознания символа
p |
|
2E |
k |
|
2h |
k |
|
|
=1−Φ |
0 |
|
|
=1−Φ |
. |
(5.55) |
||
ФМ |
|
N0 n |
|
|
0 |
|
||
|
|
|
|
|
n |
|
||
Задаваясь значениями h0 для параметров конкретного кода k , n и d0 , по формуле (5.55) вычисляют вероятности pФМ ( pЧМ или pАМ ) искажения одного символа в блоке посимвольного приема, а затем по (5.54) и (5.49) находят pПР и
QЭ .
На рис. 5.16 пунктиром нанесены кривые для симплексных кодов (7,3), (15,4), (31,5), (1023,10), совершенных кодов Хэмминга (3,1) и (7,4) и Голея
(23,12), БЧХ-кода (15,7) при использовании ФМн и посимвольной процедуре
279

приема.
Сопоставление кривых посимвольного приема с соответствующими (сплошными) кривыми оптимальной процедуры, а также безызбыточной передачи (k = n) показывает следующее.
1.Применение помехоустойчивых кодов в системах с постоянной производительностью источника менее эффективно, чем при заданном канале связи (рис. 5.17). Это объясняется тем обстоятельством, что в данном случае переход к коду с большим кодовым расстоянием, а следовательно, большим числом избыточных символов, сопровождается уменьшением энергии E1 каждого символа.
2.Посимвольный прием симплексных кодов по сравнению с оптимальной процедурой дает проигрыш 2...4 дБ в отношении сигнал/шум или 2...3 порядка в величине QЭ .
3.При малом числе информационных разрядов ряд кодов дает большую вероятность ошибки, чем в отсутствии избыточности (k = n). Таковы коды (3,1),
(7,3); код (15,4) приносит выигрыш лишь при h0 >10 .
4. Совершенные коды при посимвольном приеме дают лучшие результаты, чем симплексные. Так, код (7,4) лучше кодов (7,3) и (15,4).
Следует отметить, что при безызбыточном кодировании кодовое расстояние d0 =1 , а следовательно, посимвольный прием принципиально равноценен оптимальной процедуре.
Более подробно с вопросами помехоустойчивости систем передачи информации, использующих кодирование, можно познакомиться по работам [25].
Контрольные вопросы
1.Какая задача кодирования решается кодером канала?
2.Поясните физический смысл помехоустойчивого кода?
3.На рис. 2.21 представлена частично заполненная диаграмма сверточно-
го кода 12 . Сформируйте полную диаграмму состояний.
280
