Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Корольов / Теория связи

.pdf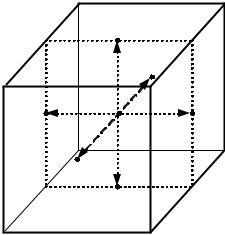

Скачиваний:

230

Добавлен:

10.02.2016

Размер:

8.73 Mб

Скачать

☆

<<< < Предыдущая 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 3940 / 4640 41 42 43 44 45 46 > Следующая >>>

В противном случае ансамбли сигналов рассматривают как объемные
упаковки. Сохранение манипуляционного кода, принятого для простого трех-
мерного куба, в значительной мере со-
храняет пропорциональность между евк-			100	(+1)	000
лидовыми и хемминговыми расстояния-

ми и поэтому будет наилучшим и для			101		(+1)
наиболее плотного ансамбля. Для других					001
комбинаций	манипуляционных	кодов	(-1)	0	(+1)
			110		010
для сигнальных векторов изначально не
			(-1)
будет соблюдаться взаимная пропорцио-
				(-1)
нальность между евклидовыми		и хем-
			111		011
минговыми расстояниями.

Таким образом, практически не-			Рис. 9.13. Поверхностно-сферическая
возможно создать идеальный манипуля-			укладка обычного куба для ФМн-8
ционный код и, следовательно, целесо-
образно строить манипуляционные коды, у которых хотя бы частично выпол-
няется взаимосвязь между евклидовыми и хемминговыми расстояниями.

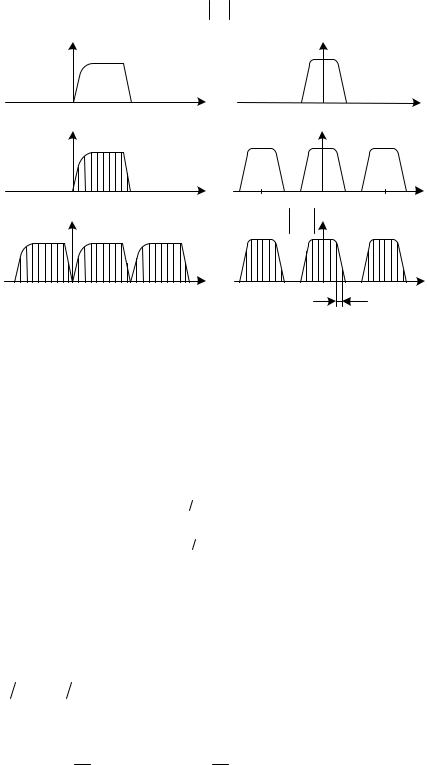
9.5. Алгоритмы цифровой обработки сигналов 9.5.1. Дискретные сигналы и их спектры

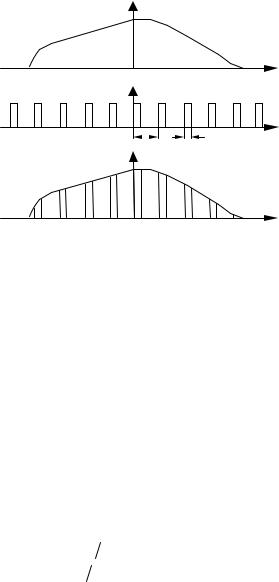
Дискретизация непрерывного сигнала. С аналитической точки зрения процедуру получения дискретизированного (дискретного) сигнала uT (t) удобно рассматривать как непосредственное умножение непрерывного сигнала u(t) на вспомогательную последовательность y(t) дискретизирующих прямоугольных

импульсов единичной амплитуды
uT (t) = u(t) y(t) .	(9.24)
Длительность дискретизирующих импульсов τи	должна быть много
меньше интервала дискретизации ∆t .

Принцип формирования дискретного сигнала показан на рис. 7.7, б…в, где изображены графики функций u(t) uT (t) y(t) . При этом реальный дискретный

сигнал uT (t) имеет вид импульсно-модулированного колебания, т. е. АИМ-

сигнала.

391

	u(t)
	а	t
	0
	y(t)
	1	t
	б	t
	б	τи
	0 ∆t	τи
	uT (t)
	в	t
	0

Рис.9.14. Дискретизация сигналов

Спектр дискретного сигнала. Чтобы дать оценку требованиям к длительности дискретизирующих импульсов, определим спектральный состав дискретного сигнала uT (t) . Пусть некоторый непрерывный сигнал u(t) имеет спектральную плотность S(ω) . Представим последовательность дискретизирующих прямоугольных импульсов y(t) рядом Фурье, в котором частота ω1 = 2π∆t :

		τ		∞
y(t) =		и 1 +		2∑Sn		cos nω1t ,			(9.25)
		∆t		n=1
где
	Sn =		sin(nω1 τи				2)	.	(9.26)
	Sn =		nω1 τи			2		.	(9.26)
			nω1 τи			2
Подставив формулу (9.25) в (9.24), получим
	τи			τи	∞
uT (t) =	τи	u(t) + 2		τи	∑Snu(t) cos nω1t .				(9.27)
	∆t			∆t	n=1

Проанализируем первое и второе слагаемые этого выражения отдельно. Первому слагаемому соответствует спектральная плотность S(ω) исходного сигнала u(t) . К произведению u(t)cos nω1t второго слагаемого применим прямое преобразование Фурье. Используя формулу Эйлера и проведя несложные математические выкладки, запишем


S( jω) = S(ω) =	∞∫u(t) cos nω1t e− jωt dt =	1	∞∫u(t) e− j(ω−nω1 )t dt +		1	∞∫u(t) e− j(ω+nω1 )t dt

	−∞	2 −∞		2		−∞
В этом выражении первый интеграл представляет собой спектральную
плотность сигнала	u(t) на частотахω	− n ω 1		а второй -		ту же спектральную

392

плотность, но на частотах ω + n ω 1

. Поэтому

∞∫u(t)cos nω1t e

− jωt dt = 1

[S(ω −nω1) + S(ω +nω1)].

(9.28)

−∞

Следовательно, дискретному сигналу вида (9.27) соответствует спек-

тральная плотность

∞

ST (ω) =

S(ω) + ∑Sn S(ω − nω1 ) + ∑Sn S(ω + nω1 ) .

(9.29)

∆t

n=1

Поскольку при n = 0 коэффициент Sn =1, запишем

∞

sin(nω τ

ST (ω) =

и ∑Sn S(ω

− nω1 ) =

∑

S(ω − nω1 ) .

(9.30)

∆t

nω τ

∆t

=−∞

			−ωВ		0	ωВ	ω
				SТ
						K0
2π		−2ω	−ω1			ω1	2ω	2π		ω
	τ	1		+ωВ		ω1 −ωВ	1		τ
	τ	И	−ω1	+ωВ		ω1 −ωВ			τ	И
		И								И

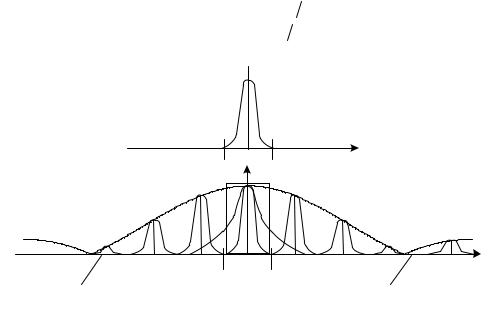
График спектра дискретного сигнала, полученного из непрерывного, показан на рис.9.15,б.

Полученные результаты позволяют сделать следующие выводы: спектральная плотность ST (ω) дискретного сигнала uT (t) представляет со-

бой бесконечную последовательность спектральных плотностей S(ω) исходного непрерывного сигнала u(t) , сдвинутых друг относительно друга на частоту

ω1 ;

огибающая спектральной плотности ST (ω) дискретного сигнала uT (t) с точностью до коэффициента 1∆t повторяет огибающую спектральной плотности дискретизирующего прямоугольного импульса.

Чтобы восстановить непрерывный сигнал u(t) из дискретного uT (t) , достаточно выделить центральную часть спектра ST (ω) . На практике это осуществляют с помощью идеального ФНЧ, имеющим коэффициент передачи

393

K (ω) = K0 , −ωв ≤ ω ≤ ωв .

(9.31)

Вместе с тем известно, что идеальный ФНЧ физически нереализуем и может служить лишь теоретической моделью для пояснения принципа восстановления непрерывного сигнала на основе теоремы Котельникова. Реальный ФНЧ имеет частотную характеристику, которая либо охватывает несколько лепестков спектра (штрих - пунктирная линия на рис. 9.15,б), либо имеет конечную крутизну ската характеристики и не полностью охватывает центральный лепесток. В практических схемах интервал дискретизации, определяемый формулой ∆t2Fв , уменьшают в 2...5 раз. В этом случае отдельные составляющие спектра дискретного сигнала не перекрываются, как это и показано на рис. 9.15, б, и могут быть разделены фильтрами.

При уменьшении длительности дискретизирующего импульса τи , амплитуды спектральных составляющих с ростом частоты убывают медленнее. В предельном случае, при τи → 0 спектр дискретного сигнала будет представлять собой бесконечную последовательность «копий» спектров исходного сигнала, имеющих равную амплитуду. Если одновременно с уменьшением длительности увеличивать амплитуду импульса так, чтобы его площадь оставалась неизменной и равной единице, то дискретизирующие сигналы преобразуются в последовательность дельта-функций:

∞
y(t) = ∑δ(t − k∆t) .
k =−∞
В этом случае формула (9.24) запишется следующим образом:
∞	∞
uT (t) = u(t) ∑δ(t −k∆t) = u(k∆t)	∑u(k∆t)δ(t −k∆t) .	(9.32)
k=−∞	k=−∞

Спектральная плотность дискретного сигнала в этом случае примет вид:

	1	∞
ST (ω) =		∑S(ω −nω1) .	(9.33)
	∆t
		n=−∞

Пример 9.1. Непрерывный сигнал, имеющий форму прямоугольного импульса напряжения с единичной амплитудой и длительностью τи , дискретизирован 10 отсчетами. Определить спектр дискретного сигнала.

Решение. Для нахождения спектра воспользуемся формулой (9.33). В ней частота ω1 = 2π∆t = 20πτи , а интервал дискретизации ∆t =τи 10 . Тогда

394

∞

sin(

ωτи

−

20nπ

τи

)

∞

sin(

ωτ

и −10nπ)

τи

ST (ω) =

∑τи

=10 ∑

∆t

ωτи

20nπ

τи

ωτи

n=−∞

−

n=−∞

−10nπ

τи

Возможность представления дискретных сигналов uT (t) в форме (9.32) существенно упрощает их анализ. В частности, спектральную плотность ST (ω) можно вычислить непосредственно по совокупности временных отсчетов {u(k∆t)}. Действительно, применив прямое преобразование Фурье

S( jω) = S(ω) = ∞∫u(t)e− jωt dt к соотношению (9.32) для отсчетов только с положи-

−∞

тельными номерами k = 0,1...,∞, со, получим с учетом фильтрующего свойства дельта-функции:

∞	∞	∞
ST (ω) = ∫	∑u(k∆t) e− jωtδ(t −k∆t)dt = ∑u(k∆t)e− jωk∆t .		(9.34)
0 k=0		k=0

При этом существенно сокращается время обработки реальных непрерывных сигналов.

9.5.2. Алгоритмы дискретного и быстрого преобразований Фурье

Как и при анализе аналоговых сигналов, дискретные сигналы можно представить во временной и частотной областях. В настоящее время обработку дискретных сигналов чаще всего проводят в частотной области, что диктуется значительными сокращениями объема цифровой аппаратуры и времени обработки.

Пусть дискретной обработке подвергается аналоговый импульсный сигнал u(t) длительностью Tи , имеющий спектральную плотность S(ω) (рис. 9.16, а, б). Теоретически можно предположить, что дискретизация сигнала производится периодической последовательностью дельта-функций

N −1
y(t) = ∑δ(t − k∆t) ,	(9.35)

k =0

где N =Tи / ∆t — требуемое число отсчетов, отвечающих теореме Котельникова.

Подставив в (9.32) пределы суммирования от 0 до N −1 , и заменив здесь и далее для упрощения и уменьшения объема формул u(k∆t) = uk , запишем выражение для дискретного сигнала (рис. 9.16, е)

395

N −1

uT (t) = u(t)∑δ(t −k∆t)

k=0

N −1
= ∑uk δ(t −k∆t) .	(9.36)

k=0

На основании формулы (9.36) можно сделать вывод, что спектр данного дискретного сигнала имеет периодическую структуру с периодом по оси частот ω1 = 2π / ∆t (рис. . 9.16, г). Мысленно продолжим дискретный сигнал периодически с интервалом Tи (рис. . 9.16, д). Сn

u				S
0	T	t		ST	0	ω
u				ST
T
unT0∆t	(N−1)∆t	t	− ω1	Сn	0	ω1 ω
−N+1 0	N−1	k	−N+1		0	N−1 n
						ωн

Рис. 9.16. Графики к выводу ДПФ:

а,б - аналоговый сигнал и его спектр; в,г - дискретный сигнал и его спектр; д - периодическая последовательность дискретного сигнала; е - ДПФ сигнала

unT (t + nTи) = uT (t) , n = 0,±1,±2,....

По аналогии с представлением периодических непрерывных сигналов

∞		1	T 2
			∫u(t) e jnω1t dt - комплексная амплитуда n -й гар-
u(t) = ∑Cne jnω1t , где	Cn =
		T
n=−∞			−T 2

моники. Дискретную функцию unT (t) можно разложить в комплексный ряд Фурье:

∞
unT (t) = ∑Cn e jnωнt ,	(9.37)

n=−∞

где ωн = 2π Ти = 2π (N ∆t) - частота дискретизации сигнала. Коэффициенты этого ряда

1 Tи

Cn = Tи ∫0 uT (t)

Tи

e jnωнt dt = T1 ∫uT (t) e j 2πntТи dt . (9.38)

и 0

Для определения коэффициентов проделаем следующее. Подставим фор-

396

мулу (9.36) в (9.38) и заменим параметр Ти = N ∆t . Введем безразмерную пере-

менную y = t / ∆t			и запишем
	1	Tи N	−1		−	π	1 N −1		N N −1	−	π
Cn =		∑ukδ(t − k∆t) e				j 2 nt Ти dt =		∑uk	∑δ( y − k) e		j 2 ny N dy .
Cn =	T	∑ukδ(t − k∆t) e				j 2 nt Ти dt =		∑uk	∑δ( y − k) e		j 2 ny N dy .
	T	∫k =0					N k =0		∫k =0
	и	0							0
Используя фильтрующее свойство дельта – функции, находим
				1		N −1
			Cn =	1		∑uk e− j 2πnk N .					(9.39)
			Cn =			∑uk e− j 2πnk N .					(9.39)
				N k =0

Это называется дискретным преобразованием Фурье (ДПФ). Дискретное преобразование Фурье по существу представляет собой алгоритм вычисления гармонических составляющих спектра Сn по заданным дискретным отсчетам uk аналогового сигнала u(t) , что значительно сокращает время обработки. Характерный вид модулей коэффициентов Сn показан на рис. 9.16,е.

Следует отметить ряд свойств ДПФ, которые вытекают из определения

(9.39).

1.Дискретное преобразование Фурье обладает свойством линейности: линейной комбинации дискретных сигналов соответствует линейная комбинация их ДПФ.

2.Коэффициент С0 представляет собой среднее значение (постоянную

составляющую) всех дискретных отсчетов сигнала

1 N −1

C0 = N ∑k =0 uk .

3. Число различных коэффициентов Сn равно числу отсчетов N за длительность сигнала Tи ; при n = N коэффициент Сn = С0 .

Пример 9.2. Определить коэффициенты ДПФ дискретизированного прямоугольного импульса единичной амплитуды, заданного четырьмя отсчетами

(N = 4) .

Решение. Используя основную формулу (9.39), вычислим пять первых коэффициентов ДПФ: С0 = 4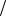4 =1;

	1	N −1	1	N −1
C1 =	1	∑(1+ e− jπ 2 + e− jπ + e− j3π 2 ) = 0 ; C2 =	1	∑(1+ e− jπ + e− j 2π + e− j3π ) = 0
	4 k =0		4 k =0
		N −1		N −1
C3 =	1	∑(1+ e− j3π 2 + e− j3π + e− j9π 2 ) = 0 ; C4	=	1 ∑(1+ e− j 2π + e− j 4π + e− j6π ) =1.
	4 k =0			4 k =0

При изучении теории ДПФ возникает очевидный вопрос: можно ли по

397

известным коэффициентам ДПФ вычислить отсчетные значения uk непрерывного сигнала? По аналогии с периодическими сигналами представим заданную периодическую последовательность отсчетов комплексным рядом Фурье. Заменив в (7.25) t = k∆t , ωн = 2π(N ∆t) и, учитывая, что суммируется конечное число членов ряда, запишем

N −1
uk = ∑Cne j 2πnk N .	(9.40)

n=0

Данное соотношение определяет алгоритм обратного дискретного преобразования Фурье (ОДПФ). Формулы (9.39) и (9.40) являются аналогами прямого и обратного преобразований Фурье для непрерывных сигналов.

Выражение (9.39) показывает, что для определения одного коэффициента ДПФ сигнальной последовательности из N отсчетов, необходимо выполнить около N операций умножения на комплексное число и столько же сложений, а для нахождения всех коэффициентов объем вычислений составит N 2 . В частности, при N = 210 =1024 надо осуществить более миллиона (10242 ) умножений и сложений. Если длины обрабатываемых массивов превышают тысячу единиц, то дискретная спектральная обработка сигналов в реальном масштабе времени требует высокопроизводительных вычислительных комплексов.

u k



а)															k


0	1	2	3	4	5	6	7	8	9	1 0	1 1 1 2 1 3 1 4 1 5
u 2 k



б )															k
б )

0		1		2		3		4		5			6	7
u 2 k + 1




в )															k
в )

	0		1		2		3		4			5	6	7
Рис.9.17. Разбиение последовательности uk													на две подпоследовательно-

сти: а - входная; б - с четными номерами; в - с нечетными номерами

Многократно сократить число операций позволяет быстрое преобразование Фурье (БПФ), обеспечивающее вычисление коэффициентов ДПФ за меньшее число операций. В основу БПФ положен принцип разбиения заданной по-

398

следовательности отсчетов дискретного сигнала на несколько промежуточных последовательностей. Для этого число отсчетов N разделяется на множители (например, N =8 = 2 2 2, N = 60 = 3 4 5 ). Затем определяются спектры этих промежуточных последовательностей и через них находится спектр всего сигнала. В зависимости от состава, числа и порядка следования указанных множеств можно создать различные алгоритмы БПФ. В цифровой технике удобно обрабатывать сигнальные последовательности со значениями N, являющимся степенью числа два (4, 8, 16 и так далее). Это позволяет многократно делить входную последовательность отсчетов на подпоследовательности.

Пусть требуется вычислить ДПФ дискретного сигнала {u(k∆t)} ={uk }, имеющего четное число отсчетов (рис. 9.17, а), причем N = 2r ; r - целое число.

Представим входную последовательность в виде двух подпоследовательностей с четными и нечетными номерами и половинным числом членов в каж-

дой (рис. 9.17, б,в): uчт = u2k ; uнч

= u2k +1 ; k = 0,1,2,..., N 2 −1.

Коэффициенты ДПФ для последовательностей с четными и нечетными

номерами запишем отдельно:

N 2−1

− j 2πnk

∑u2k e− j 2πn2k N =

∑u2k e N 2 = Cnчт

k =0

N 2−1

− j 2πnk

∑u2k +1 e− j 2πn(2k +1) N =

e− j 2πn N ∑u2k +1 e

N 2 = e− j 2πn NCnнч .

(9.41)

k =0

Коэффициенты Сn результирующего ДПФ входной последовательности

можно выразить через параметры Cnчт и Cnнч

двух вновь введенных подпосле-

довательностей. Анализ (9.41) показывает, что в диапазоне номеров отсчетов от 0 до N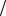2 −1, ДПФ входной последовательности определяется соотношением:

Cn = Cnчт + e− j 2πn N Cnнч , n = 0,1,2,..., N 2 −1.						(9.42)
Так как ДПФ четной и нечетной последовательностей являются периоди-
ческими, с периодом N 2 , то Cnчт = C(n+N 2)чт ; Cnнч =C(n+N 2)нч .
Запишем экспоненциальный множитель в формуле (9.42) при						n ≥ N 2 , т.е.
для ДПФ C( N 2+n)нч , в виде:
	2π (N 2+n)		2πn		2πn
e− j		= e− jπ e− j		= −e− j
	N		N		N

С учетом двух последних выражений находим коэффициенты ДПФ вход-

399

ной последовательности для отсчетов с номерами от N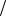2 доN −1:

CN 2+n = Cnчт −e− j2πn N Cnнч , n = 0,1,2,..., N 2 −1.

(9.43)

Соотношения (9.42) и (9.43) полностью определяют алгоритмы вычисления коэффициентов с помощью БПФ. Отметим, что экспоненциальные фазовые множители e− j 2πnN в этих алгоритмах учитывают влияние сдвига нечетной подпоследовательности относительно четной.

Чтобы еще уменьшить число вычислений, четную и нечетную подпоследовательности также разбивают каждую на две промежуточные части. Разбиение продолжают вплоть до получения простейших двухэлементных последовательностей. Определив ДПФ данных простейших пар отсчетов, можно вычислить ДПФ четырехэлементных, восьмиэлементных и так далее подпоследовательностей. При объединении ДПФ четной и нечетной подпоследовательностей используют алгоритмы (9.42) и (9.43), подставляя в них соответствующие значения номеров N и n .

Нетрудно заметить, что вычисления по формулам (9.41) не потребуют операций умножения, в (9.41) имеются только сложение и вычитание комплексных чисел. Учитываться же должны лишь операции умножения в алгоритмах (9.42) и (9.43) для различных n при разбиениях массива отчетов на мелкие подпоследовательности. Число этих операций при первом разбиении составляло N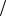2 . Такое же число N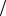2 операций требуется выполнить при каждом следующем разбиении. Таким образом, вдвое увеличивается число подпоследовательностей и вдвое сокращается наибольшее число n в формулах (7.30), (7.31).

Вычисление коэффициентов ДПФ последовательности из N отсчетов по алгоритмам БПФ требует примерно N log2 N операций умножения. Алгоритмы

БПФ сокращают число	операций по сравнению с алгоритмами ДПФ в
N 2 /(N log2 N) = N log2 N раз.	Например, при количестве отсчетов N = 210 , имеем

log2 N =10 и сокращение числа операций составляет N log2 N ≈100 . При очень больших массивах отсчетов входного сигнала выигрыш в скорости обработки может достигать нескольких тысяч.

Таким образом, в алгоритмах БПФ выполняются операции сложения и вычитания с умножением одного из компонентов на экспоненциальный множитель e− j 2πnN . Эту базовую для БПФ операцию очень удобно представлять сиг-

400

<<< < Предыдущая 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 3940 / 4640 41 42 43 44 45 46 > Следующая >>>

Соседние файлы в папке Корольов

#
10.02.2016128.38 Кб26Метод рек ТЕЗ КП.docx
#
10.02.201647.5 Кб22Практ. завд.залк..docx
#
10.02.2016330.75 Кб31ТЕК_курсова.doc
#
10.02.201620.41 Кб27Теор.пит. залк..docx
#
10.02.201615.29 Кб14Теор.питання_ТЕКС.docx
#
10.02.20168.73 Mб230Теория связи.pdf
#
10.02.201635.33 Кб13Ттул курсова робота.doc