
Корольов / Теория связи
.pdf10.1.3. Оценка стойкости криптосистем
При оценке стойкости произвольных криптографических систем защиты информации обычно придерживаются принципа Керкхоффа: стойкость криптосистемы должна быть обеспечена и тогда, когда нарушителю известно полное ее описание. Поэтому при анализе стойкости криптографической системы будем предполагать, что противоборствующей стороне известно детальное описание системы, статистические характеристики используемого языка сообщений, пространства возможных ключей и криптограмм; она может иметь некоторую информацию о контексте сообщения и т.п. Единственное, чего не не должен знать нарушитель – секретный криптографический ключ, используемый пользователями криптографической системы защиты информации [31].
Для оценки стойкости криптографических систем защиты информации используются различные подходы, среди которых наибольший интерес представляют информационно-теоретический, сложностно-теоретический и системный подходы.
В соответствии с информационно-теоретическим подходом к оценке стойкости криптографических систем они могут быть разделены на, безусловно стойкие и на условно стойкие криптосистемы. Стойкость безусловно стойких криптографических систем не зависит ни от каких возможностей нарушителя и условий ее определения и не может быть уменьшена ни при каких обстоятельствах.
Стойкость условно стойких криптографических систем зависит от возможностей противоборствующей стороны и условий ее определения, и ее оценки могут меняться в зависимости от многих факторов.
Выяснение вопроса, является ли криптосистема безусловно или условно стойкой, составляет важную задачу информационно-теоретического подхода к оценке стойкости произвольных криптографических систем защиты информации. Если в рамках информационно-теоретического подхода криптосистема признана условно стойкой, то уточнить степень ее стойкости можно с использованием сложностно-теоретического и системного подходов. В научно-
411
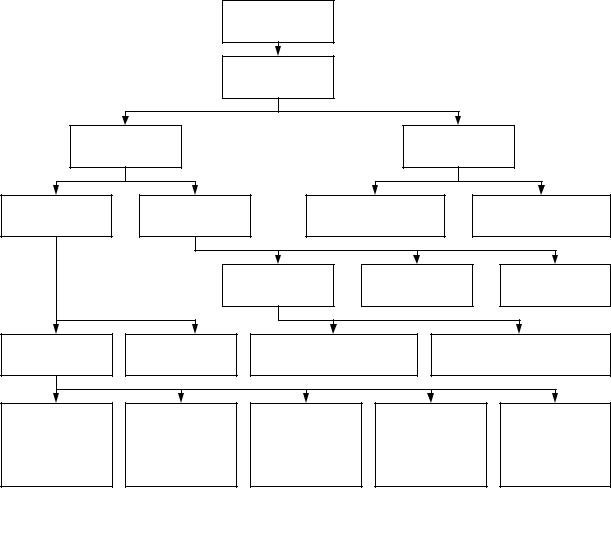
технической литературе информационно-теоретический подход иногда относят к классу теоретических подходов к оценке стойкости криптосистем, а остальные – к классу практических подходов. На рис. 10.2 приведена классификационная схема оценок стойкости криптографических систем защиты информации.
Среди средств защиты информации от возможных атак нарушителя выделяются средства криптографической защиты информации. На них могут возлагаться следующие основные задачи:
обеспечение секретности (конфиденциальности) передаваемой, обрабатываемой и хранимой информации;
обеспечение целостности передаваемой, обрабатываемой и хранимой информации;
обеспечение подлинности сообщений и корреспондентов (пользователей), а также подлинности взаимодействующих сетей и систем;
412
установление авторства передаваемых и хранимых сообщений; обеспечение доступности для законных корреспондентов (пользователей)
информации, ресурсов и услуг; обеспечение целостности самих средств криптографической защиты ин-
формации.
10.2. Функции, используемые в криптографических системах
Принципы построения криптографических систем защиты информации основаны на использовании математических функций специального вида, которые должны легко вычисляться законными пользователями, знающими «ключ»,
иочень сложно для всех не обладающих ключом.
10.2.1.Общее описание функций, используемых в криптографических системах
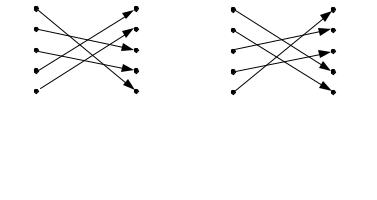
Рассмотрим пример произвольной функции y = f (x), |
которую зададим |
||||
графически |
(рис. 10.3). |
f : X →Y |
g : Y → X |
||
Пусть задано |
множество |
||||
|
|
||||
X = {a,b,c, d,e} |
и |
множество |
|
|
|
Y = {1,2,3,4,5}. |
Напомним, что |
|
|
||
функция определяется двумя |
|
|
|||
множествами |
X |
и Y , и правилом f , которое назначает каждому элементу из |
|||
множества X |
один элемент из множества Y . Множество X |
называется обла- |
|||
стью определения функции, а множество Y областью ее значений. |
|||||
Элемент y |
из множества Y является образом элемента x , а элемент x яв- |
||||
ляется прообразом y . Отображение элементов из множества X в множество Y
записывают так: f : X →Y .
Множество всех элементов y , имеющих хотя бы один прообраз, называ-
ется образом функции f и обозначается Im(f ).
Функция называется однозначной (отображением один в один), если каж-
413
дый элемент из множества Y является образом не более одного элемента из множества X . Функция f называется биекцией, если она является однозначной и Im(f )=Y . Функция вида g = f −1 называется обратной к f .
Среди биективных функций есть класс функций называемых инволюциями, которые наиболее часто используются для построения симметричных криптографических систем защиты информация.
|
Биективная функция называется инволюцией, если у функции совпадает |
||||
область определения и область ее значений, т.е. |
X =Y = S , а также обратная |
||||
{ |
|
f : S → S |
} |
функция с прямой |
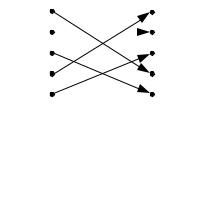
f = f −1 . Пример инволюции |
|
для множества S = {1,2,3,4,5} показан на рис. 10.4. |
||||
|
|
||||
|
|
Существование обратной функции является |
|||
|
|
||||
|
|
основой построения систем шифрования ин- |
|||
формации, с помощью которой можно однозначно дешифровать криптограммы в сообще-
ния.
Последовательное применение сначала функции шифрования, а затем функции дешифрования к произвольному сообщению x S однозначно восстанавливает данное сообщение:
10.2.2. Однонаправленные функции
Особую роль в криптографии играют однонаправленные функции, которые в общем случае не являются биективными.
Однонаправленной называется такая функция f , для которой легко опре-
делить значение функции y = f(x) , но практически невозможно отыскать для за-
данного y такое x , что y = f (x).
Для построения криптографических систем защиты информации чаще используются однонаправленные функции, для которых обратное преобразование существует и однозначно, но вычислительно нереализуемо. Они называются вычислительно необратимыми функциями.
414
В качестве примера однонаправленной функции y = f (x) рассмотрим ши-
роко известную функцию дискретного возведения в степень: y =αx (mod p), где x – целое число от 1 до p −1 включительно, а вычисление производится по мо-
дулю p , где p – очень большое простое число; α – целое число (1 <α < p ).
Напомним, что простым числом называется целое число, которое не делится ни на какие числа, кроме себя самого и единицы.
Пример 10.1. |
Для примера возьмем небольшое простое число p = 7 ; тогда |
|
для осуществления |
преобразований можно выбрать примитивный элемент |
|
α = 3 , так как |
α1(mod 7)= 3 , α2 (mod 7)= 32 (mod 7)= 9(mod 7)= 2 , α3 (mod 7)= 6 , |
|
α4 (mod 7)= 4 , α5 (mod 7)= 5 , α6 (mod 7)=1. |
||
Функция y =αx (mod p) вычисляется сравнительно просто, а обратная к ней |
||
функция x = logy |
p |
является вычислительно сложной практически для всех |
(1 < y < p ) при условии, что не только p велико, но и ( p −1 ) имеет большой про-
стой множитель (лучше всего, если это будет другое простое число, умноженное на 2). В связи с этим такую задачу называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.
Задача дискретного логарифмирования состоит в том, что для известных целых α , p , y необходимо найти целое число x . Однако алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.
По современным оценкам теории чисел при целых числах α ≈ 2664 и p ≈ 2664 решение задачи дискретного логарифмирования потребует около 1026
операций, что имеет в 103 раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.
Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.
415
Одним из первых применений однонаправленных функций было решение задачи обеспечения безопасности и использования пароля, по которому осуществляется доступ пользователя к ресурсам и услугам в автоматизированных системах.
Открытое значение y вместе с именем пользователя может быть поме-
щено в список паролей доступа, хранящихся в ЭВМ. Законный пользователь для получения доступа в автоматизированную систему предъявляет свое число x . ЭВМ вычисляет по этому числу значение однонаправленной функции y =αx (mod p) и сравнивает с хранящимся значением y . При совпадении этих значений пользователь становится идентифицированным и получает требуемый доступ.
Кроме однонаправленных функций, не имеющих вычислительно простого обратного отображения даже для законных пользователей, знающих секретную ключевую информацию, в криптографии широко используются однонаправленные функции, для которых знание секретного ключа дает возможность законному пользователю вычислительно просто находить обратное отображение. Они получили название однонаправленных функций с потайным ходом, иногда их называют однонаправленными функциями с лазейкой.
Однонаправленные функции с потайным ходом
Быстрое развитие криптографии в последние два десятилетия во многом стало возможным благодаря открытию американскими учеными В. Диффи и М. Хэлманом однонаправленных функций с потайным ходом и их использованием для различных криптосистем защиты информации [1, 31].
Однонаправленная функция с потайным ходом есть однонаправленная функция fz с дополнительным свойством, таким, что, зная информацию z по-
тайного хода для каждого вычислительно просто определить x X ,
удовлетворяющее уравнению y = fz (x).
Для нарушителя, не знающего информации z потайного хода, нахождение отображения y = fz−1(x) может быть сделано вычислительно нереализуемым.
416
Поэтому информация z может служить секретным ключом для пользователя функций с потайным ходом.
Однонаправленные функции с потайным ходом относятся к вычислительно необратимым функциям.
Функция вычислительно необратима, если при попытке формирования алгоритма нахождения обратного отображения к ней противник наталкивается на непреодолимую вычислительную проблему.
Оценивая стойкость криптосистем, построенных на основе известных однонаправленных функций с потайным ходом, отметим, что ни одна из них не является безусловно стойкой. Это объясняется тем, что нарушитель с теоретически бесконечными вычислительными ресурсами способен вычислять обратное отображение к таким функциям.
На основе однонаправленных функций с потайным ходом можно построить криптосистемы аутентификации информации в условиях взаимного недоверия корреспондентов, системы шифрования информации, в которых отправители сообщений могут пользоваться несекретными ключами шифрования, криптосистемы обмена секретной ключевой информации по открытым каналам связи, а также многие другие криптосистемы.
К настоящему времени предложено большое количество однонаправленных функций с потайным ходом, построенных на основе известных вычислительно сложных математических задач. Наиболее часто для построения однонаправленных функций с потайным ходом используется сложность решения следующих теоретико-числовых задач:
отыскание дискретного логарифма элемента в большом конечном поле или группе (криптосистема открытого распространения ключей ДиффиХэллмана, криптосистема шифрования и криптосистема цифровой подписи сообщений Эль-Гамаля, криптосистема цифровой подписи сообщений Шнорра и другие криптосистемы) [1, 31, 36];
разложение больших чисел на простые множители (криптосистема шифрования и криптосистема цифровой подписи сообщений РША, криптосистема
417
цифровой подписи сообщений Рабина и другие криптосистемы) [1, 19]; задача об укладке целочисленного ранца (класс ранцевых систем шифро-
вания информации Меркля-Хэллмана) [1, 36]; декодирование неизвестных получателю кодов Гоппы (класс систем
шифрования информации Мак-Эллиса) [1].
Рассмотрим конкретные однонаправленные функции с потайным ходом, послужившие основой для широко используемых на практике криптографических систем защиты информация.
Однонаправленная функция РША с потайным ходом
В 1978 году была предложена первая однонаправленная функция с потайным ходом, положенная в основу широко используемой на практике несимметричной криптографической системы РША. Первые буквы фамилий ее авторов (Р. Ривеста, А. Шамира и Л. Адлемара) образовали общепринятое название предложенной ими функции и криптосистемы. Для описания однонаправленной функции РША с потайным ходом требуются некоторые сведения из элементарной теория чисел [1, 19, 31].
Однонаправленная функция РША с потайным ходом определяется как дискретное возведение значения x в степень ключа e : fz (x): y = xe (modn), где z{p, g, d} – информация потайного хода; p и g являются большими простыми числами; x – положительное целое число, не превосходящее n = p g ; а значе-
ние e – положительное целое число, не превосходящее ϕ(n) – функции Эйлера,
для которого наибольший общий делитель (e,ϕ(n))=1.
Пусть fz (x) имеет обратную функцию вида fz−1(y): x = yd (mod n), где значе-
ние d есть единственное положительное целое, меньшее ϕ(n) и удовлетворяю-
щее условию d e =1(modϕ(n)).
Исследования однонаправленной функции РША с потайным ходом показали, что практически все попытки противостоящей стороны получить информацию о потайном ходе эквивалентны разложению n = p g на множители. По-
этому в последние десятилетия интенсивно исследовались методы разложения
418
составного числа на множители. В математике такая задача называется задачей факторизацией составного числа и в течение столетий она привлекала внимание многих ученых. Известный наилучший алгоритм факторизации составного числа имеет субэкспоненциальную вычислительную сложность.
За последние годы в области разработки эффективных методов факторизации достигнуты существенные успехи, поэтому для обеспечения требуемой безопасности применения однонаправленной функции РША с потайным ходом должны использоваться числа p и g ‚ размерностью многие сотни и даже тыся-
чи бит.
Однонаправленная функция Эль-Гамаля c потайным ходом
Ранее была рассмотрена однонаправленная функция на основе вычисления дискретных логарифмов в алгебраической группе. Поле Галуа GF(p), где p
– простое число, является более сложной алгебраической структурой по сравнению с группой, над его элементами можно выполнять операции сложения и умножения, а в группе - только сложение или только умножение. Например, рассмотренная ранее однонаправленная функция Диффи и Хеллмана, послужившая основой криптосистемы открытого распространения ключей, использует операцию умножения над элементами группы [1, 31, 36].
Задача вычисления дискретных логарифмов в алгебраическом поле формулируется следующим образом. При заданных простом числе p , порождаю-
щем поле GF(p), и примитивном элементе g |
( 0 < g < p ) по элементу y поля |
отыскать элемент x ( 0 ≤ x < p −1) такой, |
что выполняется тождество |
y = g x (mod p). |
|
Число x является ключом формирования цифровой подписи сообщений отправителя и должно храниться отправителем сообщений в секрете, а значение у сообщается всем как открытый ключ проверки цифровой подписи сообщений отправителя.
На основе однонаправленной функции Эль-Гамаля с потайным ходом, как для функции РША, можно построить несимметричную систему шифрования информации.
419
Безопасность использования однонаправленной функции Эль-Гамаля с потайным ходом основана на вычислительной сложности задачи дискретного логарифмирования в алгебраическом поле большой размерности. Объем вычислений для ее решения выше, чем при факторизации составного числа.
Однонаправленная функция с потайным ходом на основе алгебраических уравнений по модулю 2
|
Значение однонаправленной функции f (x) с потайным ходом зависит от |
аргументов M и K : |
|
|
C = f (M , K )= (Md −1, Md ), |
где |
M – вектор сообщения, состоящий из двух частей M0 и M 1 длиной по n |
бит каждая: M = (M0 , M1 ); K – вектор ключа, который определяется совокупно- |
|
стью подвекторов: K ={K1, K2 ,..., Kd −1}. |
|
|
Над вектором M циклически выполняются d раз операции вида: |
|
Mi = Mi−2 f (Mi−1Ki−1 ), 2 ≤ i ≤ d , |
где |
f ( ) – некоторое фиксированное нелинейное преобразование, а знак |
означает сложение по модулю два.
Рассмотренный принцип построения однонаправленной функции с потайным ходом используется при построении широкого класса блочных систем шифрования (класс блочных шифров Фейстеля) к которому принадлежат известный американский алгоритм шифрования данных DES и отечественный алгоритм шифрования согласно ГОСТ 28147–89 [1, 31, 36].
10.2.3. Криптографические хэш-функции
Понятие хэш-функций было определено в 1979 году в работах американского математика Р. Меркля, однако еще ранее в автоматизированных системах широко использовались некриптографические хэш-функции для оптимизации размещения и поиска данных [1, 31].
Хэш функции (хэширующие функции (ХФ)) произвольного вида принадлежат к классу однонаправленных функций без потайного хода.
420
