
Лосев-КлячинМиклюков МА в КИ
.pdf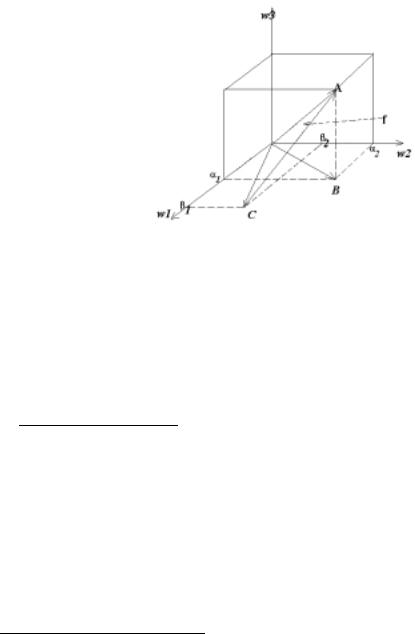
§4. Свойство минимальности отрезков ряда Фурье |
391 |
Устремляя n → ∞, получаем
∞ |
|
b |
|
a |
|
|
|
|
|
|
|
m=0 αm2 |
≤ |
f2(x)dx. |
(7) |
Данное соотношение называется неравенством Бесселя5.
ЗАМЕЧАНИЕ. Теорема 4.1 допускает следующую геометрическую интерпретацию.
|
S2(x) = α1ω1(x) + α2ω2(x) |
|
|
T2(x) = β1ω1(x) + β2ω2(x) |
|
|
|
|
b
(f(x) − S2(x))2dx — длина перпендикуляра AB.
a
b
(f(x) − T2(x))2dx — длина отрезка AC
a
Теорема 4.1 утверждает, что длина перпендикуляра не больше длины наклонной.
ЗАМЕЧАНИЕ. Из неравенства Бесселя (7) вытекает, что
∞
ряд αn2 сходится. Таким образом общий член ряда αn → 0
n=0
при n → ∞, т.е. коэффициенты Фурье кусочно-непрерывной функции стремятся к 0.
5Бессель Фридрих Вильгельм (22.7.1784 – 17.3.1846) – немецкий астроном. Род. в Миндене (Германия). В 20 лет вычислил орбиту кометы Галлея. Работал в Кенигсберге (ныне Калининград). При обработке астрономических наблюдений широко применял теорию вероятностей и способ наименьших квадратов.




396 Глава 16. Ряды Фурье
Кроме того, справедливы следующие равенства
|
x+π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x π |
|
|
sin((n + 1 )(t |
|
|
|
x)) |
|
|
t |
|
|
|
x = τ |
|
|
|
||||||||||||||||
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(t) |
|
|
sin2t−2x |
− |
|
|
dt = |
|
dt−= dτ |
|
|
= |
|
||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
sin(n + 21 )τ |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
= |
|
f(x + τ) |
|
|
|
|
|
|
|
|
dτ = |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
sin τ2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
f(x + τ) |
sin(n + 21 )τ |
dτ + |
|
f(x + τ) |
sin(n + 21 )τ |
dτ. (3) |
|||||||||||||||||||||||||||
|
sin τ2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin τ2 |
|
|
|
||||||||
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кроме того |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
0 |
|
|
|
|
|
sin(n + |
1 )τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
π |
|
|
|
τ = −t |
|
|
|
|
||||||||||||||||||||||||
|
− |
|
f(x + τ) |
|
|
τ |
2 |
|
|
dτ = |
|
|
= |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
sin 2 |
|
|
|
|
|
|
|
dτ = −dt |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= − π |
0 |
|
|
|
|
|
sin(n + 21 )( |
− |
t) |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
f(x − t) |
|
|
|
|
|
|
|
|
dt = |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
sin −2t |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= |
0 |
f(x |
− |
t) |
sin(n + 21 )t |
dt. |
|
|
(4) |
||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Объединяя равенства (3) и (4), получаем |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 )τ |
|||
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin(n + |
||||||||||
|
Sn(x) = |
|
(f(x + τ) + f(x − τ)) |
|
|
|
|
2 |
|
dτ, |
||||||||||||||||||||||||
|
2π |
|
|
|
sin τ2 |
|
|
|||||||||||||||||||||||||||
что и требовалось доказать.
§6. Теорема о локализации
Следующая теорема показывает, что поведение частичных сумм ряда Фурье в точке x зависит лишь от значений функции в сколь угодно малой окрестности этой точки, т.е. от локального строения функции в этой точке.


398 |
|
|
|
|
|
|
|
|
|
Глава 16. Ряды Фурье |
||
|
|
π |
|
|
|
|
|
π |
|
|
|
|
= |
1 |
|
q(τ) cos |
τ |
1 |
|
q(τ) sin |
τ |
||||
|
|
sin(nτ)dτ + |
|
|
cos(nτ)dτ = |
|||||||
2π |
2 |
2π |
2 |
|||||||||
|
|
−π |
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
I |
+ I . |
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
Так как функции q(τ) cos τ2 |
и q(τ) sin τ2 |
являются кусочно- |
||||||||||
непрерывными, то In и In являются n-ми коэфициентами Фурье этих функций. А потому стремятся к нулю при n → ∞. В результате получаем требуемое утверждение. 
§7. Представление 2π-периодической функции рядом Фурье
ЛЕММА 7.1. Пусть f(x) удовлетворяет условию Липшица на конечном интервале (a, b), т.е. существует такая константа k, что для всех x , x (a, b) выполнено
|f(x ) − f(x )| ≤ k|x − x |.
Тогда ее можно продолжить по непрерывности на [a, b]. Причем продолженная функция также удовлетворяет условию Липшица.
Доказательство. Несложно показать (покажите!), что из условия Липшица следует выполнение условий критерия Коши существования предела функции в точке. Таким образом, на основании критерия Коши, получаем существование следующих величин
( ) ≡ x |
|
a+0 |
f(x), |
f(b) |
≡ x |
b 0 |
(1) |
f a |
lim |
|
lim f(x). |
|
|||
|
→ |
|
|
|
|
→ − |
|
Следовательно, функция f(x) продолжима по непрерывности. Поэтому для доказательства леммы нам достаточно проверить, что
|f(x) − f(a)| ≤ k|x − a|, x [a, b], |f(x) − f(b)| ≤ k|x − b|, x [a, b].
Пусть y (a, b) – произвольная точка. Тогда выполнено
|f(x) − f(y)| ≤ k|x − y|.
Переходя в данном неравенстве к пределу при y → a + 0 или y → b−0 и пользуясь соответствием (1) получаем нужное. 
§7. Представление 2π-периодической функции рядом Фурье |
399 |
ОПРЕДЕЛЕНИЕ 7.1. Будем говорить, что f(x) кусочнолипшицева на [a, b], если существует такое разбиение [a, b] на
отрезки [a, x1], [x1, x2], . . . [xn−1, b], что на каждом из отрезков разбиения функция f(x) удовлетворяет условию Липшица. При этом при определении липшицевости на частичном сегменте [xk−1, xk] в качестве значений функции на концах сегмента следует брать предельные значения f(xk−1 + 0) и
f(xk − 0).
Будем говорить, что f(x) — кусочно-липшицева на всей числовой прямой (−∞, ∞), если она обладает этим свойством на всяком отрезке [a, b].
ЛЕММА 7.2. Если f(x) — кусочно-липшицева, то для всех точек x0 существуют конечные пределы
lim f(x) = f(x0 ± 0).
x→x0±0
Доказательство. Данное утверждение сразу следует из Леммы 7.1. 
ТЕОРЕМА 7.1. Пусть f(x) — 2π-периодическая и кусочно-липшицева функция. Тогда для всех x0 ее ряд Фурье имеет конечную сумму S(x0), причем
S(x0) = |
f(x0 + 0) + f(x0 − 0) |
. |
(2) |
2 |
|
|
|
Доказательство. Как было доказано ранее (теорема 5.4):
|
|
|
π |
|
sin(n + 21 )t |
|
||
Sn(x) = |
|
1 |
0 |
[f(x + t) + f(x − t)] |
dt. (3) |
|||
π |
2 sin( |
t |
) |
|||||
|
2 |
|
||||||

400 |
Глава 16. Ряды Фурье |
Точно так же, как в параграфе "Интеграл Дирихле" можно доказать (докажите!), что
|
π |
|
|
|
|
|
2 |
0 |
sin(n + 21 )t |
dt = 1. |
(4) |
||
π |
|
t |
|
|||
2 sin( |
) |
|
||||
2 |
|
|||||
Из (3) и (4) следует, что для произвольного x0:
Sn(x0) − f(x0 + 0) + f(x0 − 0) = 2
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
0 |
[f(x0 + t) + f(x0 − t)] − [f(x0 + 0) + f(x0 − 0)] |
|
sin(n + 21 )t |
dt |
≡ |
||||||||
|
|
|
|
|
t |
|
|||||||||
|
π |
|
|
|
2 |
|
|
|
|
sin |
|
||||
|
|
|
|
|
|
|
|
2 |
|||||||
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
≡ |
1 |
0 |
g(t) sin(n + |
1 |
)tdt, |
|
||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
π |
2 |
|
||||||||||
где
f(x0 + t) − f(x0 + 0) + f(x0 − t) − f(x0 − 0) g(t) = 2 sin 2t .
Покажем, что функция g(t) принадлежит классу F[0, π]. Так как f(x) кусочно-липшицева, то на всяком отрезке [a, b] эта функция имеет конечное число точек разрыва I-го рода.
Рассмотрим сначала случай, в котором x0 является точкой непрерывности f(x). Тогда функция g(t) имеет конечное число точек разрыва на (0, π]. Покажем интегрируемость g(t) на отрезке [0, π]. Так как g(t) кусочно-непрерывна, то достаточно показать, что g(t) ограничена в окрестности точки t = 0.

