
Лосев-КлячинМиклюков МА в КИ
.pdf
§5. Ряды с неотрицательными членами |
301 |
ПРИМЕР 1. Исследуем на сходимость ряд
∞ 1 n=2 (ln n)p .
Если p ≤ 0, то ряд расходится, поскольку нарушено необходимое условие сходимости.
Пусть p > 0. Сравнивая этот ряд с гармоническим рядом, получаем (проверьте!)
|
|
1 |
|
|
n |
|
nlim |
|
(ln n)p |
|
= nlim |
= ∞. |
|
|
1 |
|
(ln n)p |
|||
→∞ |
n |
|
→∞ |
|
|
|
По теореме сравнения заключаем, что данный ряд расходится. 
ПРИМЕР 2. Исследуем на сходимость ряд
∞ 1
n=2 (ln n)ln n
.
Мы имеем
(ln n)ln n = nln ln n > n2 для достаточно больших n.
Отсюда,
1 |
< |
1 |
. |
ln n |
2 |
||
(ln n) |
n |
||
По теореме 5.3 ряд сходится. 

ТЕОРЕМА 5.4. Ряд
∞ 1
n=2 n(ln n)p
сходится при p > 1 и расходится при p ≤ 1.
Доказательство. Если p ≤ 0, то
1 |
1 |
|
|
≥ |
|
n(ln n)p |
n |
|
и, сравнивая данный ряд с гармоническим, убеждаемся, что ряд расходится. Поэтому пусть p > 0. В этом случае последовательность {n(ln n)p} является возрастающей:
n(ln n)p ≤ (n + 1)(ln(n + 1))p,


§5. Ряды с неотрицательными членами |
303 |
Таким образом, для достаточно больших n справедливо неравенство
|
|
(1 + n1 )s − 1 |
|
< r, |
|||||||
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
или |
|
|
n |
|
|
|
|
|
|
|
|
1 + |
1 |
|
s |
|
|
|
|
r |
|||
|
|
< 1 + |
|||||||||
|
|
|
|
|
. |
||||||
|
n |
|
n |
||||||||
Следовательно |
|
an |
|
|
|
|
|
1 s |
|||
|
|
|
|
|
|
|
|||||
|
|
|
> (1 + |
|
) . |
||||||
|
|
an+1 |
n |
||||||||
Последнее неравенство можно переписать следующим образом
an+1 |
|
n |
s |
|
|
1 |
|
|
|
||
< |
|
= |
|
(n+1)s |
|
. |
|||||
|
|
|
|
|
1 |
|
|||||
an |
n + 1 |
|
|
|
|
|
|
||||
|
|
|
|
ns |
|||||||
Применяя теорему сравнения 4.3 и признак сходимости обобщенного гармонического ряда, получаем сходимость ряда в первом случае.
Пусть теперь n( an − 1) ≤ 1. Тогда
an+1
an+1 |
|
n |
|
1 |
|
|
|
≥ |
= |
n+1 |
. |
||||
an |
n + 1 |
1 |
|||||
|
|
|
|
|
n |
||
Применяя теорему сравнения 4.3, получим требуемое.
СЛЕДСТВИЕ (Признак Раабе в предельной форме).
Пусть lim Rn = R. Тогда при R > 1 ряд сходится, при R < 1
n→∞
ряд расходится.
ТЕОРЕМА 5.7. Пусть an ≥ 0.Тогда если an = O( |
1 |
) при |
|||||||
ns |
|||||||||
|
ns |
|
→ ∞ |
|
≤ |
|
|
|
|
n → ∞ и s > 1, то ряд |
n = 1an сходится. |
|
|
|
|
||||
Если же |
1 |
= O(an) при n |
|
и s |
|
1, то ряд |
|||
|
|
|
|||||||
расходится.
Доказательство. Для доказательства в теореме сравнения достаточно взять обобщенный гармонический ряд. 
Следствие. Пусть lim nαan = k. Тогда
n→∞
1) если α > 1 и 0 ≤ k < +∞, то ряд n = 1an сходится,
2)если α ≤ 1 и 0 < k ≤ +∞, то ряд расходится.
Вчастности, если an n1α , то ряд сходится при α > 1 и расходится при α ≤ 1.

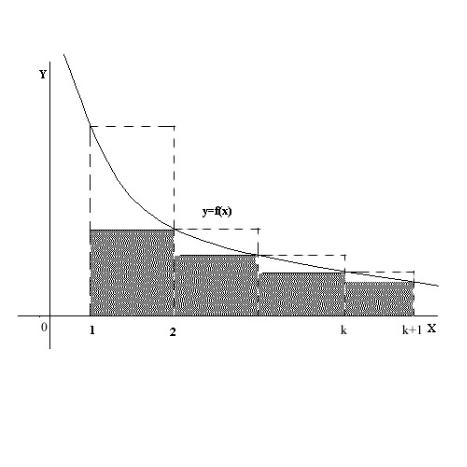
§6. Интегральный признак сходимости |
305 |
n
Полагая Sn = f(k), имеем
k=1
n
f(k + 1) = f(2) + f(3) + . . . + f(n + 1) = Sn+1 − f(1).
k=1
Пользуясь формулой Ньютона-Лейбница, получаем
Sn ≥ F (n + 1) − F (1) ≥ Sn+1 − f(1).
На основании условия сходимости положительных рядов, делаем нужные заключения. Теорема доказана. 
СЛЕДСТВИЕ (другая формулировка интегрального признака сходимости). Если функция f(x), определенная
при всех x ≥ 1, неотрицательна и убывает, то ряд
∞
f(n)
n=1
сходится тогда и только тогда, когда сходится интеграл
∞
f(x)dx.
1

306 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Глава 13. Числовые ряды |
|
ПРИМЕР 1. Исследуем на сходимость ряд |
|
|||||||||||||||||||||||||||
|
|
|
|
|
∞ |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
− ln(1 + |
|
|
) . |
|
||||||||||||||
|
|
|
|
|
n=1 |
n |
|
n |
|
|||||||||||||||||||
Рассмотрим на [1, +∞) вспомогательную функцию |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y = |
|
− ln(1 + |
|
). |
|
|
||||||||||||||||
|
|
|
|
|
x |
x |
|
|
||||||||||||||||||||
Прежде всего, как известно (проверьте!), |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
ln(1 + ε) ≤ ε |
|
|
|||||||||||||||||||
для всех ε (−1, +∞). Поэтому |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
− ln(1 + |
|
|
) ≥ |
|
|
− |
|
|
|
= 0. |
|
||||||||||||
|
|
x |
x |
x |
x |
|
||||||||||||||||||||||
Далее, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
1 |
|
(−1/x2) |
= |
|
1 |
|
+ |
|
|
1 |
< 0 |
|||||||||||||||
|
|
|
−x2 |
(x + 1)x |
||||||||||||||||||||||||
|
−x2 |
− 1 + 1/x |
|
|
|
|
|
|
||||||||||||||||||||
при x > 0 и, стало быть, y(x) монотонно убывает. Воспользуемся интегральным признаком сходимости. Най-
дем первообразную |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
x |
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|||||||
F (x) = 1 |
|
|
|
|
− ln(1 + |
|
) |
dt = ln x − 1 |
ln(1 + |
|
) dt = |
||||||||||||||||||||||||||
|
t |
t |
t |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
1/t2 |
|
|
|
1 |
|
|||||||||
= ln x − x ln(1 + x1 ) + ln 2 + 1 |
|
|
t · |
|
− |
dt = ln x − x ln(1 + |
|
)+ |
|||||||||||||||||||||||||||||
1 + 1/t |
x |
||||||||||||||||||||||||||||||||||||
|
|
|
x dt |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
+ ln 2 − 1 |
|
|
= ln x − x ln(1 + |
|
|
) − ln(x + 1) + 2 ln 2 = |
|||||||||||||||||||||||||||||||
|
t + 1 |
x |
|||||||||||||||||||||||||||||||||||
ln |
x |
− x ln x+1x + 2 ln 2 = −(x + 1) ln(1 + x1 ) + 2 ln 2. |
|||||||||||||||||||||||||||||||||||
x+1 |
|||||||||||||||||||||||||||||||||||||
Далее находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(1 + |
1 ) |
|
|
|
|
|
|
||||||||
|
|
|
lim |
F (x) = 2 ln 2 |
− x |
lim |
|
|
|
|
|
|
|
|
x |
|
= |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
|
+ |
∞ |
|
|
|
|
|
+ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x+1 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
→ |
|
|
|
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
− |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
x2 |
|
|
|
|
|
|
|
= 2 ln 2 |
− |
1, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
= 2 ln 2 − x→+∞ (1 + x1 ) · |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
(x+1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
т.е. ряд сходится. 

§7. Признаки сходимости Коши и Даламбера |
307 |
ПРИМЕР 2. Исследуем на сходимость ряд
∞ 1
n=1 ns .
Конечно, этот ряд нам уже хорошо известен, однако воспользуемся другим методом его исследования. Пусть вначале s > 0, s = 1. Воспользуемся интегральным признаком:
f(x) = |
|
1 |
, F (x) = |
x dt |
= |
x1−s − 1 |
, |
|||||
|
|
1 |
|
|
|
|
|
1 − s |
||||
|
|
xs |
|
ts |
|
|
|
|||||
|
|
lim F (x) = lim |
|
x1−s |
. |
|
||||||
|
|
|
|
|
||||||||
|
x→∞ |
x→∞ 1 − s |
|
|||||||||
Таким образом при s > 1 предел конечен, и ряд сходится, а при s < 1 предел бесконечен, и ряд расходится. Пусть теперь s = 1 (т.е. рассматривается гармонический ряд). Тогда
F (x) = ln x,
lim ln x = +∞.
x→+∞
То есть в данном случае ряд расходится. 

§7. Признаки сходимости Коши и Даламбера
Ниже мы будем пользоваться понятиями верхнего и нижнего пределов последовательности, введенными ранее. Напомним их определения.
ОПРЕДЕЛЕНИЕ 7.1. Пусть {an}∞n=1 – прoизвольная последовательность. Говорят, что a есть верхний предел {an}∞n=1 и пишут
a = limn→∞an, (или a = lim supn→∞an),
если
i) существует подпоследовательность {ank } → a;
(иначе, ε > 0 N n > N : |an − a| < ε)
ii) ε > 0 N(ε) : n > N(ε) выполнено an < a+ε. Говорят, что a есть нижний предел an и пишут
a = limn→∞an, (или a = lim infn→∞an),
если
i)существует подпоследовательность {ank } → a;
ii)ε > 0 N(ε) : n > N(ε) выполнено an > a−ε.

308 |
Глава 13. Числовые ряды |
УПРАЖНЕНИЕ 1. Проверьте следующие утверждения.
1)limn→∞n(−1)n = +∞, limn→∞n(−1)n = 0.
2)limn→∞ n1 = limn→∞ n1 = 0.
3)limn→∞(−1)nn = +∞, limn→∞(−1)nn = −∞.
4)limn→∞ n+1n = +1, limn→∞ n+1n = +1.
Всюду в данном параграфе будем считать, что an = 0 для всех номеров n.
ТЕОРЕМА 7.1 (Признак Коши). Пусть задан ряд
∞
|
|
|
an |
(1) |
||
|
|
n=1 |
|
|||
и пусть |
n |
|
|
|
||
|
|
|
|an| |
= a. |
|
|
|
limn→∞ |
|
||||
Тогда
i) если a < 1, то ряд (1) сходится; ii) если a > 1, то ряд (1) расходится;
iii) существуют как сходящиеся, так и расходящиеся ряды, для которых a = 1.
Доказательство. Рассмотрим случай i), т.е. a < 1. Зададим произвольно ε > 0 так, чтобы a + ε < 1. По определению верхнего предела найдется номер N(ε) такой, что при всех n > N(ε) будет выполнено
n |
|
< a + ε < 1. |
|
|an| |
|
||
Тогда для произвольного n > N(ε) имеем |
|
||
|an| < (a + ε)n. |
(2) |
||
Ряд
∞
(a + ε)n
n=1
есть геометрическая прогрессия со знаменателем (a + ε) < 1. Пользуясь теоремой сравнения, заключаем на основании (2), что ряд (1) сходится.
ii) Пусть a > 1. Из определения верхнего предела заключа-
ем, что существует подпоследовательность nk |ank | → a > 1.
Значит, |an| > 1 для бесконечного числа значений n. Тем самым, нарушено необходимое условие сходимости ряда: an →
0.




