Приведем еще один аналогичный пример.
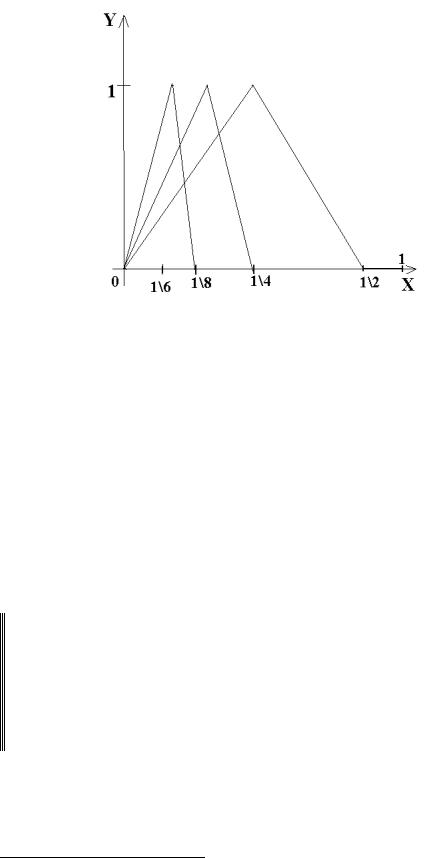
ПРИМЕР 3. Рассмотрим последовательность функций, изображенную на графике.
Последовательность этих функций на [0, 1] сходится к функции, тождественно равной нулю. Сходимость неравномерная, но предельная функция непрерывна, следовательно условие равномерной сходимости ряда не является необходимым для заключения о непрерывности предельной функции. 

§5. Теорема Дини
ТЕОРЕМА 5.1 (Дини1). Пусть E R – замкнутое ограниченное множество. Кроме того, пусть {fn(x)} – последовательность функций, непрерывных на E, сходящаяся (поточечно) на E к непрерывной функции f(x).
Если для всех n выполнено fn(x) ≥ fn+1(x) x E, то {fn(x)} сходится к f(x) равномерно на E.
Доказательство. Положим gn(x) = fn(x) − f(x) ≥ 0. Тогда
все gn(x) непрерывны, gn(x) ≥ gn+1(x) и gn(x) → 0 поточечно. Таким образом, нам достаточно показать, что gn(x) сходится к 0 равномерно на E.
1Дини Улисс (14.11.1845-28.10.1918) – итальянский математик. Родился и работал в Пизе (Италия). Ему принадлежат важные работы по теории функций действительного переменного, теории аналитических функций, алгебре, аналитической теории дифференциальных уравнений.
342 |
Глава 14. Функциональные последовательности и ряды |
Т.к. последовательность {gn(x)} монотонно убывает на E, то для доказательства ее равномерной сходимости достаточно показать, что для любого ε > 0 найдется хотя бы один номер n = n(ε) такой, что
0 ≤ gn(x) ≤ ε x E.
Предположим противное, т.е.
ε > 0 n = 1, 2, ... xn : gn(xn) > ε > 0.
Так как множество E ограничено, то по теореме БольцаноВейерштрасса из последовательности {xn} можно извлечь подпоследовательность {xnk }, сходящуюся к некоторой точке x0, которая принадлежит множеству E, в силу его замкнутости.
Мы имеем gnk (xnk ) > ε > 0. Зафиксируем целое m ≥ 0.
Тогда nk ≥ m выполнено gm(xnk ) ≥ gnk (xnk ) > ε > 0, т.е. gm(xnk ) > ε > 0. Переходя здесь к пределу при nk → ∞
получим gm(x0) ≥ ε > 0. Переходя к пределу при m → ∞,
получаем lim inf gm(x0) ≥ ε > 0, что противоречит поточеч-
m→∞
ной сходимости последовательности функций gm(x) к 0.
УПРАЖНЕНИЕ 1. Сформулируйте и докажите аналогичную теорему для неубывающей функциональной последовательности.
ПРИМЕР 1. Последовательность {xn} сходится неравномерно на [0, 1), что показывает существенность требования замкнутости множества E в условиях теоремы. 

ПРИМЕР 2. Последовательность {nx } сходится неравномер-
но на R+, что показывает существенность требования ограниченности множества E в условиях теоремы. 

ПРИМЕР 3. Последовательность {xn} сходится неравномерно на [0, 1], что показывает существенность требования непрерывности предельной функции в условиях теоремы. 
УПРАЖНЕНИЕ 2. Найдите пример, показывающий существенность требования монотонности в условиях теоремы.
|
∞ |
ТЕОРЕМА 5.2. Пусть дан ряд |
Un(x) определенный |
n=1
на замкнутом ограниченном множестве E. Предположим, что все Un(x) непрерывны и неотрицательны. Тогда, если ряд имеет непрерывную сумму S(x), то этот ряд сходится к ней равномерно на множестве E.
Доказательство – очевидно, проведите его самостоятельно.
n→∞ x→x0
§6. Перестановка предельных переходов |
343 |
§6. Перестановка предельных переходов в равномерно сходящейся последовательности
ТЕОРЕМА 6.1. Пусть последовательность {fn(x)} равномерно сходится к f(x) на множестве E. Кроме того, пусть x0 – предельная точка множества E и для любого номера n существует конечный
lim fn(x) = An. |
(1) |
x→x0 |
|
|
Тогда последовательность {An} сходится и |
|
lim f(x) = lim An |
|
x→x0 |
n→∞ |
|
или, в развернутом виде,
lim lim fn(x) = lim lim fn(x).
x→x0 n→∞
ПРИМЕР 1. Последовательность {xn} сходится неравномерно на [0, 1). Кроме того, справедливы соотношения
lim lim xn = 1
n→∞ x→1
и
lim lim xn = 0.
x→1 n→∞
Таким образом, условие равномерной сходимости в теореме существенно. 

Доказательство. Выберем произвольно ε > 0. Согласно критерию Коши, найдется N такое, что для всех n, m > N и для всех x E выполнено
|fn(x) − fm(x)| < ε.
Переходя в этом равенстве к пределу при x → x0, получаем
|An − Am| ≤ ε.
Тем самым, по критерию Коши для числовых последовательностей, получаем существование
lim An = A.
n→∞
Нам достаточно показать, что существует
lim f(x) = A.

344 |
Глава 14. Функциональные последовательности и ряды |
Фиксируем произвольное ε > 0. Тогда найдется номер n0 такой, что для всех x E выполнено
|f(x) − fn0 (x)| < |
ε |
, |
(2) |
3 |
что возможно в силу равномерной сходимости последовательности. Учитывая определение предела числовой последовательности, и выбирая, если нужно n0 еще больше, добьемся того, чтобы было выполнено
Из условия (1) следует существование δ(ε) > 0 такого, что для всех x E, x = x0, |x − x0| < δ(ε) выполняется
|fn0 (x) − An0 | < |
ε |
(4) |
3. |
Объединяя (2), (3), (4) получаем, что для произвольного ε > 0 нашлось δ(ε) > 0 такое, что для всех x E, x = x0, |x − x0| < δ(ε) выполнено
|f(x)−A| ≤ |f(x)−fn0 (x)|+|fn0 (x)−An0 |+|An0 −A| < |
ε |
+ |
ε |
+ |
ε |
= ε, |
|
|
|
|
3 |
3 |
3 |
т.е. |
|
|
|
|
|
|
|
lim f(x) = A. |
|
|
|
|
|
|
|
x→x0 |
|
|
|
|
|
|
|
Таким образом, теорема доказана. |
|
|
|
|
|
|
|
Аналогично устанавливается следующая теорема.
|
∞ |
ТЕОРЕМА 6.2. Пусть дан ряд |
Un(x), определенный |
n=1
на множестве E, и x0 – предельная точка множества E. Пусть этот ряд сходится равномерно на E и пусть для всех натуральных n существует
lim Un(x) = Un.
x→x0
∞
Тогда ряд
n=1
иначе говоря
|
→ |
n |
|
|
|
∞ |
∞ |
Un сходится, причем lim |
Un(x) = |
Un, |
|
x x0 |
=1 |
n=1 |
∞ |
∞ |
|
|
|
|
|
|
lim Un(x) = |
lim Un(x). |
|
x→x0 n=1 |
n=1 x→x0 |
|
|
§7. Равномерная сходимость и интегрирование |
345 |
§7. Равномерная сходимость и интегрирование
ТЕОРЕМА 7.1. Пусть {fn(x)} – последовательность непрерывных функций, равномерно сходящаяся на [a, b] к f(x). Тогда справедливо равенство
|
a |
b |
b |
lim |
f (x)dx = |
f(x)dx. |
n→∞ |
n |
a |
Доказательство. Всюду ниже будем считать, что a < b. Прежде всего отметим, что предельная функция f(x) является непрерывной. Зададим произвольно ε > 0. В силу равномерной сходимости {fn(x)} к f(x) на [a, b], существует N(ε) такое, что для всех n > N(ε) и для всех x [a, b] справедливо неравенство
−ε < fn(x) − f(x) < ε.
Интегрируя данное неравенство находим:
b b
−ε(b − a) < fn(x)dx − f(x)dx < ε(b − a)
a a
т.е. для всех n > N(ε) выполнено
b b
|fn(x)dx − f(x)dx| < ε(b − a).
a |
|
|
|
a |
Это означает, что |
|
|
|
|
|
a |
b |
|
b |
lim |
f |
|
(x)dx = f(x)dx, |
n→∞ |
|
n |
a |
что и требовалось доказать.
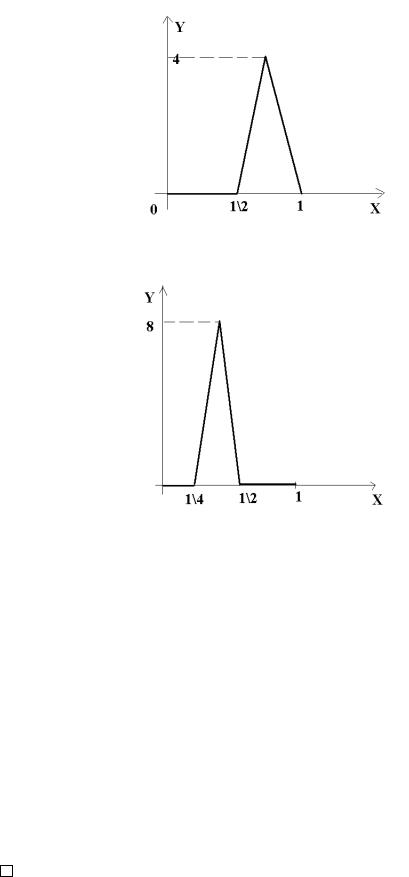
ПРИМЕР 1. Рассмотрим последовательность функций, изображенную на графиках.
Обратим внимание, что
1
f1(x) = 1.
346 |
последовательности и ряды |
Обратим внимание, что
1
f2(x) = 1.
0
Остальные функции строятся аналогично. Данная последовательность функций сходится поточечно на отрезке [0, 1] к непрерывной функции f(x) = 0. С другой стороны справедливы соотношения
1 1
lim |
0 |
f (x)dx = 1 = 0 = |
0 |
lim f (x)dx. |
n→∞ |
n |
|
n→∞ n |
УПРАЖНЕНИЕ 1. Сформулируйте и докажите аналогичную теорему для рядов.

§8. Равномерная сходимость и дифференцирование |
347 |
ЗАМЕЧАНИЕ. Требование непрерывности {fn(x)} не является существенным в условиях теоремы, его можно заменить, например, на интегрируемость. Попробуйте сформулировать соответствующую теорему и доказать ее (или разобраться с доказательством, используя другую учебную литературу).
§8. Равномерная сходимость и дифференцирование
ТЕОРЕМА 8.1. Пусть {fn(x)} – последовательность непрерывно дифференцируемых на [a, b] функций. Предположим, что
1.последовательность {fn(x)} сходится к f(x) поточечно на [a, b];
2.последовательность {fn(x)} сходится к ϕ(x) равномерно на [a, b].
Тогда предельная функция f(x) имеет производную, при-
чем
f (x) = ϕ(x).
Доказательство. Пусть x0 [a, b] – произвольная точка. Т.к. все fn(x) непрерывны, то по предыдущей теореме имеем:
x0 x0
lim |
a |
f |
x |
dx |
|
a |
ϕ |
x |
dx. |
n→∞ |
n( |
) |
|
= |
( |
) |
|
Таким образом, по формуле Ньютона-Лейбница, получаем
x0
lim f |
x |
0) − |
f a |
)) = a |
ϕ x |
dx. |
n→∞( n( |
|
n( |
( ) |
|
Но, с другой стороны, fn(x) → f(x) поточечно и, значит,
|
|
|
|
|
|
|
|
|
x0 |
|
lim f |
x |
0) − |
f a |
|
f |
x |
0) − |
f a |
a |
ϕ t dt. |
n→∞( n( |
|
n( |
)) = |
( |
|
( ) = |
( ) |
Точка x0 выбиралась произвольно, и поэтому
x
f(x) − f(a) = ϕ(t)dt
348 |
Глава 14. Функциональные последовательности и ряды |
для всех x [a, b].
Функция ϕ(x) непрерывна, поскольку является предельной для равномерно сходящейся последовательности непрерывных функций. Дифференцируя интеграл по переменному верхнему пределу получаем:
|
|
x |
|
|
|
ϕ(x) = |
d |
a |
ϕ(t)dt = |
d |
(f(x) − f(a)) = f (x), |
|
|
dx |
dx |
что и доказывает теорему.
ПРИМЕР 1. Положим
x fn(x) = 1 + n2x2 ,
где x [−1, 1]. Данная последовательность сходится на [−1, 1] (и притом равномерно) к функции f(x) ≡ 0 (докажите!).
Рассмотрим последовательность производных
|
|
|
|
|
|
|
|
|
f |
(x) = |
1 + n2x2 − x(2xn2) |
= |
(1 − n2x2) |
. |
n |
|
(1 + n2x2)2 |
|
(1 + n2x2)2 |
|
|
|
Легко показать, что |
|
|
|
|
|
|
|
lim f x |
) = |
0, |
при x = 0 |
|
n→∞ n( |
1, |
при x = 0 |
а
lim fn(x) = 0.
n→∞
Таким образом, в теореме нельзя отказаться от равномерной сходимости производных, даже если предположить равномерную сходимость самих функций. 

ЗАМЕЧАНИЕ. Условия теоремы можно ослабить. Достаточно потребовать дифференцируемость fn(x), вместо первого пункта потребовать сходимость {fn(x)} хотя бы в одной точке отрезка [a, b] и второй пункт теоремы оставить без изменений. Тогда можно утверждать, что эта последовательность сходится во всем промежутке (причем равномерно), и предельная функция дифференцируема, причем
f (x) = lim fn(x).
n→∞
Однако доказательство в таких предположениях мы проводить не будем. Желающим предлагаем разобраться самостоятельно.
Un(x) сходится равномерно на [a, b] к некоторой функ-
§9. Степенные ряды |
349 |
|
∞ |
ТЕОРЕМА 8.2. Пусть дан ряд Un(x) составленный |
|
n=1 |
из непрерывно дифференцируемых на [a, b] функций, схо-
дящийся к S(x) (поточечно). Кроме того, пусть ряд
∞
n=1
ции H(x). Тогда S(x) имеет производную в каждой точке [a, b], причем для всех x [a, b] выполнено S (x) = H(x).
Доказательство. Данное утверждение сразу следует из предыдущей теоремы, и его доказательство предлагаем провести самостоятельно. 
§9. Степенные ряды
ОПРЕДЕЛЕНИЕ 9.1. Пусть задана последовательность вещественных чисел {cn}. Ряд
∞
n=0
называется степенным рядом. Числа {cn} называются коэффициентами степенного ряда.
Ясно, что при изучении ряда вида (1) достаточно ограничиться изучением его разновидности:
∞
cnxn. (2)
n=0
ТЕОРЕМА 9.1 (Коши-Адамара2). Пусть задан степенной ряд (2). Положим
|
|
|
|
|
|
|
|
1 |
. |
|
α |
= |
lim sup n c |
, |
R = |
|
|
|
|
n→∞ | |
n| |
|
α |
Тогда ряд (2) сходится и притом абсолютно при всех x таких, что
|x| < R,
и расходится при всех x, для которых
|x| > R.
2Адамар Жак (8.12.1865-17.10.1963) – французский математик, член Парижской АН, иностран-

350 |
Глава 14. Функциональные последовательности и ряды |
Доказательство. Зафиксируем x и положим an = cnxn. Рас-
смотрим числовой ряд
∞
|
|
|
|
|
|
|
an. |
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
Заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
n→∞ |
|
|
|
|
|
| |
| n→∞ |
|
|
|
| |
| |
|
| |
n| |
| |
n|| | |
n = |
| |
n| |
= |
α. |
lim sup n a |
|
|
= lim sup n |
c |
x |
|
x lim sup n c |
|
|
x |
Согласно признаку сходимости Коши для числового ряда (3), этот ряд сходится при |x|α < 1, т.е. |x| < α1 , и расходится при |x|α > 1, т.е. |x| > α1 ,. Учитывая, что ряд (3) сходится
тогда и только тогда, когда сходится ряд (2), получаем утверждение теоремы. 
ЗАМЕЧАНИЕ. Данная теорема верна также и для рядов с комплексными членами. В этом случае неравенство |z| < R описывает круг радиуса R на плоскости. Поэтому как в комплексном, так и в вещественном случаях, R называется
радиусом сходимости степенного ряда.
УПРАЖНЕНИЕ 1. Сформулируйте и докажите "теорему Даламбера-Адамара".
ПРИМЕР 1. Вычислить радиус сходимости для следущих степенных рядов:
1) |
∞ |
n |
x |
n |
2) |
∞ |
|
xn |
|
3) |
|
∞ xn |
|
|
|
∞ |
|
xn |
|
|
|
|
n=0 |
n |
|
|
|
|
n=0 |
n! |
|
n=1 |
n |
|
|
|
4) |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
R = |
1 |
= 1 = 0, |
|
|
|
|
|
|
|
n nn |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
= lim sup |
|
| |
|
|
= lim sup |
= |
∞ |
; |
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
n |
→∞ |
|
|
|
| |
|
|
n |
|
| |
| |
|
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т.е. ряд сходится в единственной точке x = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
α = lim sup n |
|
1 |
| |
|
|
= lim sup |
| |
|
1 |
|
| |
= 0; R = |
|
1 |
= |
∞ |
, |
т.е. |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n→∞ |
|n! |
|
|
|
n→∞ |
|
√n! |
|
|
|
|
|
0 |
|
|
ряд сходится в каждой точке числовой прямой. |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
R |
|
, |
т.е. ряд сходится на интервале |
|
|
|
|
|
n |
|
|
|
|
3) |
lim sup √ |
n |
= 1; |
|
|
|
|
= 1 |
|
|
n→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(−1, 1). В x = +1 ряд расходится, а в точке x = −1 по признаку Лейбница сходится условно.
4) lim sup √1 = 1; R = 1, т.е. ряд сходится всюду на
n→∞ n n2
интервале (−1, 1) и, очевидно, сходится в концевых точках интервала.
ный член АН СССР. Родился в Версале (Франция). Работал в Бордо и Париже. Известен фундаментальными исследованиями в теории чисел, теории дифференциальных уравнений, классическом анализе и теории функций, вариационном исчислении.