Жолобов Ввведение в Математическое 2008

После того, как объем производства перегруженной зоны полностью исчерпывается, соответствующий пункт производства исключается из рассмотрения – просто вычеркивается соответствующая строка таблицы.

Процедура закрепления объектов выполняется только для перегруженных зон. Если таких зон нет, алгоритм не работает – нужно переключиться, например, на МНС.

Итак, алгоритм сводится к поиску перегруженных зон и закреплению за ними объектов. Затем такие зоны исключаются, и решается, по существу, новая задача – для оставшихся пунктов производства и пунктов потребления, потребности которых не удовлетворены.

Шаг 1. Распределение объектов по зонам.

Шаг 2. Если зона одна, то эта зона не может быть перегружена, так как имеет место закрытая транспортная задача. Объем производства этой зоны распределяется в соответствии с потребностями. Конец. Иначе - поиск перегруженной зоны. Если такой зоны нет, конец: план нужно искать другим методом, например, МНС.

Шаг 3. Вычисление приоритетов для объектов перегруженной зоны.

Шаг 4. Закрепление объектов за пунктом производства перегруженной зоны в порядке невозрастания приоритетов до исчерпания всего объема производства. В процессе закрепления объектов выполняются следующие действия:

1.Если потребность очередного объекта удовлетворена, а запас зоны не израсходован, объект вычеркивается. Переход к следующему (в порядке невозрастания приоритетов) объекту.

2.Если потребность очередного объекта удовлетворена частично,

азапас исчерпан, зона (пункт производства) вычеркивается. Очередной объект остается с объемом потребления, равным нехватке. Выполняется шаг 1.

3.Если потребность очередного объекта полностью удовлетворена, а объем производства зоны исчерпан, зона вычеркивается, а объект остается с нулевой потребностью. Выполняется шаг 1.

241

Пример 2.7

1. Разбили объекты по зонам.

2. Начинаем с первой зоны (в нее вошли объекты 2,4): b2+b4=15+10=25 > a1 =15. Зона перегружена.

3. Вычисляем приоритеты объектов 2 и 4: P2=7-0=7; P4=18-11= =7, т.е. в зону 1 можно включить как второй, так и четвертый объект. Включаем второй. Потребность=15, запас=15.

4. Принимаем x12=15. Исключаем зону 1, а второй объект оставляем с нулевой потребностью.

Табл. 2

Разбили объекты по зонам.

Начинаем со второй зоны (в нее вошли объекты 2,3): b2+b3=0+15=15 < a2 =25. Зона не перегружена. Рассматриваем третью зону (объекты 1,4): b1+b4=5+10=15 > a3 =5. Зона перегружена.

Вычисляем приоритеты объектов 1 и 4: P1=12-0=12; P4=20-18= 2. В зону 3 включаем первый объект. Потребность=5, запас=5.

Принимаем x31=5. Исключаем зону 3, а первый объект оставляем с нулевой потребностью.

242

Табл. 3

Осталась одна зона. Т.е. распределять объекты по зонам не нужно. Распределяем объем производства 25 ед. между 1, 2, 3, 4 объектами в соответствии с потребностью этих объектов.

Значение Z=335. Как и в методе Фогеля.

2.2.9. Использование второй теоремы двойственности для обоснования метода потенциалов

Метод потенциалов является точным методом решения транспортной задачи. Своим обоснованием этот алгоритм обязан теории двойственности в линейном программировании.

В разделе 1.3 были рассмотрены математические модели вза- имно-двойственных задач. В частности, рассматривалась пара задач:

ние двойственной задачи. Необходимым и достаточным условием того, что эти решения являются оптимальными, является выполнение всех приведенных ниже равенств:

(a1 j y1 +a2 j y2 +... + amj ym −cj )xj =0 для всех j =1,n .

Нас будет интересовать только одна сторона этого утверждения, а именно.

243

Если нестрогие неравенства двойственной задачи, соответствующие базисным переменным опорного решения прямой задачи при подстановке координат решения двойственной задачи обратятся в строгие равенства, то эти решения – оптимальные.

xij 0 ( i 1, m , j 1,n ).

Каждому из ограничений первой группы (i-му ограничению) поставим в соответствие переменную ui ( i 1, m ). Назовем ее по-

тенциалом строки.

Каждому из ограничений второй группы (j-му ограничению) поставим в соответствие переменную vj ( j 1,n ). Назовем ее по-

тенциалом столбца.

Эти же обозначения используем при построении двойственной задачи.

задачи, а y (u1 ,u2 ,...,um , v1, v2 ,...,vn ) – некоторый план двойственной задачи.

Из второй теоремы двойственности следует, что если для всех базисных переменных решения x (x11, x12 ,..., xmn ) имеет место:

то x (x11, x12 ,..., xmn ) и y (u1 ,u2 ,...,um , v1, v2 ,...,vn ) – оптимальные решения соответствующих задач.

Теперь представим себе, что мы имеем некоторый опорный

план прямой задачи x (x11, x12 ,..., xmn ) .

Основная идея метода потенциалов заключается в попытке искусственно сконструировать план двойственной задачи и проверить, выполняются ли условия второй теоремы двойственности.

Конструирование плана осуществляется следующим образом. Известно, какие переменные в решении x (x1, x2 ,..., xn ) являются базисными (заполненные клетки таблицы). Для заполненных клеток должны выполняться соотношения (2.18): ui vj cij .

Допустим, что эти соотношения выполняются. Попытаемся найти компоненты решения y (u1 ,u2 ,...,um , v1, v2 ,...,vn ) . Что любо-

пытно: всего уравнений m+n-1 (количество заполненных клеток), а количество неизвестных – m+n. Следовательно, чтобы решить систему уравнений, нужно зафиксировать одну из неизвестных, придав ей конкретное значение (например, положив u1 0 ). Осталь-

ные определятся однозначно.

Теперь имеем компоненты решения (пока это – просто век-

тор) y (u1 ,u2 ,...,um , v1, v2 ,...,vn ) , причем условия (2.18) выполняются автоматически.

Проверим выполнение условий (2.19). Для каждой свободной переменной (не заполненной клетки) должно выполняться

ui vj cij .

Эта проверка в методе потенциалов сводится к вычислению

косвенных стоимостей:

Eij cij (ui vj ) ,

и к анализу знаков полученных величин.

Теперь, если оказалось, что все Eij 0 (или, что эквивалентно, ui vj cij ), то полностью выполнены условия второй теоремы, и решение x (x11, x12 ,..., xmn ) – оптимальное.

245

В противном случае (существует Eij 0 ) решение x не явля-

ется оптимальным, а построенное нами решение y – вообще не

допустимое.

Итак, способ проверки любого опорного решения транспортной задачи на оптимальность есть.

Пример 2.8

Проверим на оптимальность решение, полученное методом Фо-

геля.

По заполненным клеткам составим и решим систему уравнений:

E11=10-(0-7)=17, E13=20-(0+0)=20, E21=12-(9-7)=10

E22=7-(9+0)= -2!, E32=14-(7+0)=7, E33=16-(7+0)=9.

Решение не оптимальное, так как E22= -2 < 0.

Рассмотрим теперь вопрос перехода к новому, лучшему опорному решению в методе потенциалов.

246

2.2.10. Переход к новому опорному решению в методе потенциалов

Пусть при проверке очередного опорного решения обнаружилось, что Eij 0 , т.е. рассматриваемое решение не оптимально.

Для косвенной стоимости справедливо следующее утвержде-

ние:

косвенная стоимость Eij – это коэффициент, с которым

свободная переменная xij входит в ЦФ, если все базисные переменные выразить через свободные18.

В этой связи становится ясно, какую переменную нужно вводить в состав базисных, чтобы получить новое, лучшее опорное решение: переменную с отрицательной косвенной стоимостью (желательно, с максимальной по абсолютной величине отрицательной косвенной стоимостью).

Ответим теперь на вопрос, а какую переменную следует выводить из состава базисных?

Пусть E 0 . Вводим переменную x в состав базисных

переменных. Придадим этой переменной некоторое положительное приращение > 0. То есть потребуем, чтобы из пункта в пункт было отправлено продукции в количестве единиц. На-

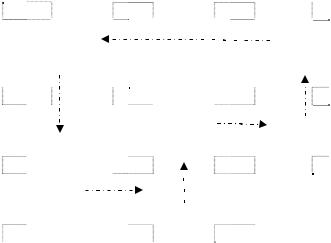
зовем клетку с координатами ( , ) положительной вершиной. Теперь рассмотрим рис. 2.7.

18 Вспомним определение оценки свободного вектора в симплекс-методе.

247

Рис.2.7. Приращение значения в свободной клетке

Отправить в -й пункт единиц продукции можно только уменьшив поставку из пункта в в другие пункты на единиц.

Найдем заполненную клетку (базисную переменную) в той же строке. Пусть это будет x j1 . Уменьшим поставку в пункт j1 на

единиц. Теперь поставка в этот пункт составляет ( x j1 ) единиц.

Соответствующую вершину назовем отрицательной.

Недопоставка в пункт j1 на единиц компенсируется за счет другого пункта – это занятая клетка того же столбца. Пусть это бу-

дет xi1 j1 . Теперь поставка в этот пункт составляет ( xi1 j1 ) еди-

ниц. Соответствующую вершину назовем положительной.

Но это можно сделать только за счет недопоставки единиц в другой пункт – на рис.2.7 этим пунктом является пункт j2. Умень-

шим поставку в пункт j2 на единиц. Теперь поставка в этот пункт составляет ( xi1 j2 ) единиц. Соответствующую вершину назовем

отрицательной. В итоге образуется последовательность вершин x , x j1 , xi1 j1 ,…, продолжающаяся до тех пор, пока очередной по-

248

ложительной вершиной не станет исходная незанятая клетка, соответствующая переменной x .

Образовался цикл пересчета, все вершины которого, кроме одной, соответствуют базисным переменным. В разделе 2.2.11 будет показано, что такой цикл – единственный для конкретной свободной клетка в данной транспортной таблице.

Переход к новому опорному решению в методе потенциалов производится следующим образом.

Начнем увеличивать . Исходное значение переменной x – это нуль (свободная переменная). Соответственно, с увеличением

значение этой переменной будет увеличиваться. Будут увеличиваться также значения базисных переменных, соответствующих положительным вершинам построенного цикла пересчета. Значения базисных переменных, не входящих в цикл пересчета, будут оставаться неизменными.

Что же касается переменных, связанных с отрицательными вершинами, их значения начнут уменьшаться. Ввиду того, что новое решение должно быть опорным и, естественно, допустимым,

можно увеличивать только до тех пор, пока значение одной или нескольких переменных, связанных с отрицательными вершинами цикла пересчета, не обратится в нуль. Соответствующую переменную, очевидно, нужно выводить из состава базисных переменных. При этом, если в нуль обращаются несколько переменных, из базиса нужно выводить только одну из них. Остальные же такие переменные должны остаться в составе базисных с нулевыми значениями: новое опорное решение в этом случае является вырожденным опорным решением.

Итак, предельное значение – это минимальный объем перевозок, найденный в отрицательных вершинах цикла.

Пусть xks – минимальный объем перевозок, найденный в од-

ной из отрицательных вершин цикла пересчета. Эта величина и будет представлять собой искомое предельное значение – значение переменной x , которая в новом опорном решении вводится в

состав базисных переменных. Значения базисных переменных, соответствующих вершинам цикла, корректируются – увеличиваются

249

или уменьшаются на величину xks . При этом переменная xks ,

принявшая нулевое значение, выводится из состава базисных переменных нового опорного решения – соответствующая клетка таблицы объявляется незанятой.

Если кроме xks после пересчета некоторые другие базисные

переменные обращаются в нуль, в соответствующие клетки записывается нуль, и они объявляются «условно-занятыми».

Увеличение на величину xks переменных, соответствую-

щих положительным вершинам цикла пересчета, и уменьшение на эту же величину переменных, соответствующих отрицательным вершинам, называется сдвигом по циклу пересчета.

Пример 2.9

Дана транспортная таблица, в которой записано некоторое опорное решение.

Здесь 6=m+n-1=3+4-1 заполненных клеток, соответствующих базисным переменным.

По заполненным клеткам составим систему уравнений для нахо-

Для удобства последующих вычислений занесем полученные результаты в новую таблицу.

250