Жолобов Ввведение в Математическое 2008

j 1

нарушает общности задачи, так как в противном случае знак минус всегда можно отнести к числителю.

Для этой задачи характерны следующие свойства. Как и в случае задачи ЛП, своего максимального значения ЦФ (1.105) достигает в одной из вершин выпуклого многогранника, определяемого ограничениями (1.106) и (1.107) (естественно, при условии, что задача имеет решение). Если же ЦФ принимает максимальное значение более, чем в одной вершине, то она достигает это значение в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Эти свойства хорошо иллюстрируются путем геометрической интерпретации задачи ДЛП.

1.5.1. Геометрическая интерпретация задачи дробно-линейного программирования

Рассмотрим случай двух переменных:

Z c1 x1 c2 x2 max d1 x1 d2 x2

ai1x1 ai2 x2 ai (i=1,2,...,m) x1, x2 0

181

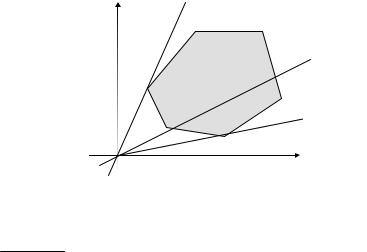
Будем считать, что в области допустимых решений (D) имеет место d1x1+ d2x2 0.

Для того чтобы найти решение задачи, сначала построим многогранник решений, определенный ограничениями задачи

(рис.1.24).

x2 Z=Zmax

Z = h

Z=Zmin

x1

Рис.1.24. Геометрическая интерпретация задачи ДЛП

Положим значение ЦФ равным некоторому числу h. То есть ЦФ будет принимать одно и то же значение во всех точках прямой

c1 x1 c2 x2 h или d1 x1 d2 x2

(с1-d1h)x1+(с2-d2h)x2=0. (1.108)

Очевидно, что эта прямая проходит через начало координат. Для того чтобы найти допустимые решения, на которых ЦФ принимает значение h, прямая должна иметь общие точки с многоугольником.

Начнем увеличивать параметр h. Увеличение этого параметра приведет к вращению прямой (1.108) вокруг начала координат либо по, либо против часовой стрелки, в зависимости от сочетания параметров cj , dj (j=1,2).

Из геометрических соображений ясно, что если допустимое множество ограничено, при некотором значении h=h* прямая (1.108) станет опорной к допустимому множеству. При этом в точке (точках) касания будет достигнуто искомое оптимальное решение.

182

B

A

x1

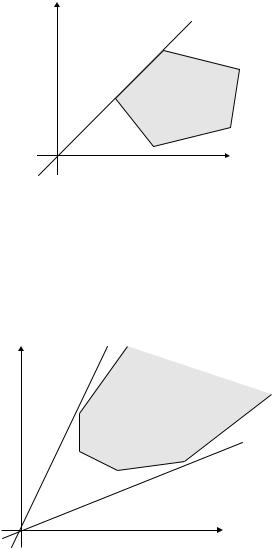
Рис.1.25. Случай бесконечного количества оптимальных решений

На рис. 1.25 представлен случай, когда максимум ЦФ достигается в любой точке отрезка [A,B].

Представляет интерес случай, когда допустимое множество не ограничено. Здесь возможны следующие ситуации.

A) Допустимое множество не ограничено, однако существуют вершины, в которых ЦФ принимает соответственно максимальное и минимальное значение (рис.1.26).

x2 Fmax

Fmin

x1

Рис.1.26. Пример задачи ДЛП для случая А

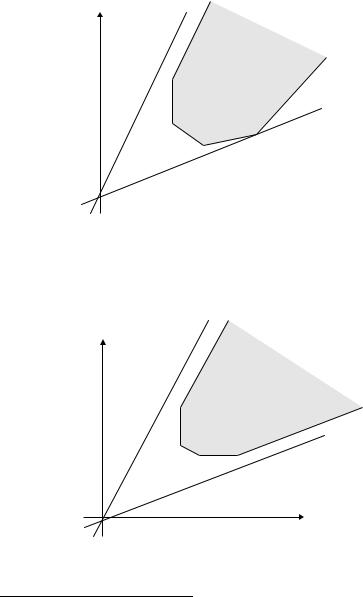
B) Допустимое множество не ограничено, и один из экстремумов не достигается. Например, минимум достигается в одной из вершин, а максимум не достигается вообще (рис.1.27).

183

x2 Fmax

Fmin

x1

Рис.1.27. Случай асимптотического максимума

Это – случай асимптотического максимума.14

В принципе, возможна ситуация, когда имеет место и асимптотический максимум и асимптотический минимум (рис.1.28).

Fmax

x2

Fmin

x1

Рис.1.28. Случай асимптотического максимума и минимума

14 Будет большой ошибкой, если этот случай считать случаем неограниченности ЦФ сверху. Здесь ЦФ ограничена сверху, но граница эта недостижима!

184

Теперь исходная задача приобретает следующий вид:

Это – задача линейного программирования. Решив эту задачу любым известным методом, всегда можно восстановить оптимальное решение исходной задачи (1.109)-(1.111).

Пример 1.30

Решить задачу ДЛП:

xj 0, j=1 4.

Производим замену переменных: yj = y0 xj .

Приходим к следующей эквивалентной задаче ЛП:

yj 0, j=0 4.

Переходим к М-задаче (одновременно вектор A3 делаем единичным базисным вектором, умножая на "-1" первое уравнениеограничение):

yj 0, j=0 5.

Решим эту задачу, для разнообразия придав M конкретное большое значение 100.

186

187

1.5.3. Задача ДЛП со свободными членами в числителе и знаменателе

Задача со свободными членами имеет вид

n

c0 cj xj

n

решений системы уравнений (1.115) имеет место d0 d j x j 0 .

задача приобретает следующий вид:

188

имеет место d0+ d1x1+ d2x2 0.

Положим значение ЦФ равным некоторому числу h. То есть ЦФ будет принимать одно и то же значение во всех точках прямой

Для того чтобы найти допустимые решения, на которых ЦФ принимает значение h, прямая должна иметь общие точки с многоугольником допустимых решений.

Начнем увеличивать параметр h. Увеличение этого параметра приведет к вращению прямой (1.119) вокруг некоторой точки

x (x1, x2 ) либо по, либо против часовой стрелки, в зависимости от сочетания параметров cj , dj (j=0,1,2).

189

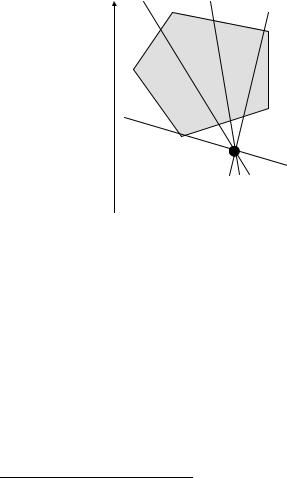
Координаты точки x (x1, x2 ) определяются следующим образом15 (рис.1.29):

x1 c0 d2 c2 d0 ,

c1d2 c2 d1

x2 c1d0 c0 d1 .

c1d2 c2d1

x2

x ( x1 , x 2 )

x1

Рис.1.29. Геометрическая интерпретация задачи ДЛП со свободными членами

Из геометрических соображений ясно, что, если допустимое множество ограничено, при некотором значении h=h* прямая (1.119) станет опорной к допустимому множеству. При этом в точке (точках) касания будет достигнуто искомое оптимальное решение.

Контрольные вопросы и задачи к разделу 1.5

1. Как при решении задачи дробно-линейного программирования интерпретировать случай, когда перменная y0=0 в оптимальном решении эквивалентной задачи линейного программирования?

15 Действительно, если h=0, то c0 c1x1 c2 x2 0. Если h= , то d0 d1x1 d2 x2 0.

Решаем систему из двух уравнений с двумя неизвестными. Получаем решение.

190