
Жолобов Ввведение в Математическое 2008
.pdf
L |
L |
Размерность этой задачи ( rk ) n . Здесь |
rk – общее коли- |
k 0 |
k 0 |
чество ограничений.
Будем считать, что в задаче имеется один блок-связка AX=B0 и один-единственный диагональный блок DX=B*.
B1 |
|
|
|
|
B |
|
, а |
D – матрица, имеющая блочно- |
|
Здесь B*= |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
BL |
|
|
||
диагональную структуру. Эта матрица состоит из L диагональных блоков.
D=
Теперь задачу можно записать следующим образом:
n
c j x j max
j 1
AX B0
DX B* x 0.
Для простоты положим, что {x DX B* , x 0} – ограничен-
ное не пустое множество. Кроме того, пусть:
{x AX B0 , DX B* , x 0} .
Как известно, любую точку ограниченного выпуклого множества можно представить, как выпуклую линейную комбинацию экстремальных точек (вершин).
То есть, если x1 , x2 , ... , xk – координаты вершин множества {x DX B* , x 0}, то это множество состоит из всех возможных точек вида:
141

k |
l |
|
|
k |
|
(1.92) |
|
|
|
||||
l x |
, где l 0 (l 1,k ) и l 1. |
|||||
l 1 |
|
|
|
l 1 |
|
|
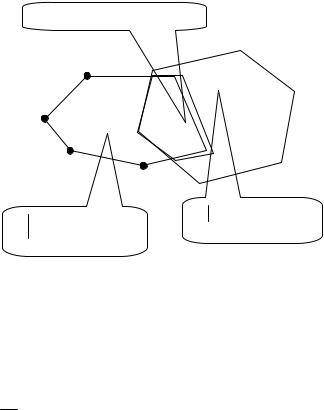
Очевидно, что любая точка, представленная в виде (1.92), |
||||||
удовлетворяет всем ограничениям DX B* , |
x 0 (рис. 1.20). |
|||||
2 |
{x DX B* , x 0} |
x |
|
x1 |
x |
xk |
xk 1 |
Рис.1.20. Иллюстрация множества DX B*
Здесь xl (x1l , x2l ,..., xnl ) .
Это обстоятельство позволяет видоизменить исходную задачу таким образом, что из рассмотрения будут исключены все ограничения диагонального блока.
Примем обозначения:
c (c1,c2 ,...,cn ) – вектор коэффициентов ЦФ;
А=(А1,А2, ... ,Аn) – матрица, составленная из векторов блокасвязки.
Теперь задача приобретает следующий вид:
|
k |
|
max |
|
||
|
cxl l |
|
||||
|
l 1 |
|
|
|
|
|
|
k |
|
|
ограничений |
||
|
Axl l B0 r0 |
|||||
|
l 1 |
|
|
|
(1.93) |
|
|
k |
|
|
|
|
|
|
l |
1 |
|
|
|
|
|
l 1 |
|
(l |
|
|
|
|
l 0, |
1,k |
) |
|
||
|
|
|
142 |
|
||
Доп. множество исх. задачи
x2 |
|
x1 |
|
xk |
k 1 |
|
x |
{x DX B* , x 0} |
{ x AX B 0 , x 0} |
|
Рис.1.21 Допустимое множество исходной задачи
Как видно, все ограничения, составляющие диагональный
L
блок DX B* , исчезли. А таких ограничений r !
1
k
Добавилось же только одно – l 1.
l 1
Но в новой задаче появились новые переменныеl 0 (l 1,k ) . Их количество – количество всех вершин.
Там не менее ясно, что найдя значения этих переменных, можно найти и решение исходной задачи:
X k l xl . l 1
Задачу, соответствующую этой новой формулировке (1.93) будем называть главной, или, что то же самое, координирующей задачей.
143

Упростим обозначения:
l |
cl ; Pl |
|
Axl |
; P0 |
|
B0 |
|
||
cx |
|
1 |
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
||
Пришли к следующей задаче:
|
k |
|
|
|
|
cl l max |
|||
|
l 1 |
|
|
|
|
k |
|
|
|
|
Pl l P0 |
|||
|
l 1 |
|
|
|
|
|
|
|
|
|
(l 1, k). |
|||
l 0, |
||||
|
|
|
|
|
r0 1.
(1.94)
Пример 1.26
2x1+3x2 max
x1+x2 15 -3x1+x2 9 4x1 -x2 8
x1,2 0.
Будем считать, что блок-связка в этой задаче представлен единственным (первым) ограничением. Диагональный блок – вторым и третьим ограничениями. Т.е.
2x1 3x2 |
max, |
<c,x> max : с=(2,3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||
x1 x2 |
15 |
AX B0 |
: A=(1,1); |
B0=(15) |
|
|
|
|||||||||||
3x1 x2 |
9 |
DX B |
* |
: |
|
3 |
1 |
|
|
|
x1 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
||||||||||||
4x1 x2 |
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
||||
8 |
|
|
|
|
4 |
1 |
|
|
|
|
|
|
|
|
8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x1,2 0 |
|
x 0. |
|
x1 |
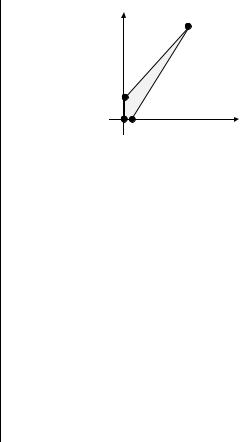
Множество DX B* , x 0 имеет 4 вершины: |
|||
=(0,0) с1=((2,3),(0,0))=0 |
|
|
||
x2 |
=(0,9) |
с2=((2,3),(0,9))=27 |
|
|
x3 =(17,60) с3=((2,3),(17,60))=214 |
|
|||
x4 |
=(2,0) |
с4=((2,3),(2,0))=4 |
|
|
144
x2 x3
x2
x1 |
x4 |
x |
|
|
1 |
P0 |
|
|
B0 |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆl |
|
|
(1,1) |
0 |
|
|
0 |
|
|
|
|
|
(1,1) |
|
0 |
|
|
9 |
|
|
|
Pl |
|
Ax |
: P1 |
|
|
|
|
|
|
|
P2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
|
|
|
; |
|
|
|
9 |
|
|
|
; |
||||||
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
17 |
|
77 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
P3 |
(1,1) |
|
|
|
|
|
P4 |
|
(1,1) |
|
|
|
2 |
|
||||||
|
|
|
|
|
|
60 |
|
|
|
|
; |
|
|
|
|
|
0 |
|
. |
|||||
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Координирующая задача имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
0 1 |
27 2 |
214 3 |
4 4 |
max |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
0 1 |
9 2 |
77 3 2 4 15 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
1 |
2 |
|
3 |
4 1 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
( j |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
j |
0, |
1, 4). |
|
|
|
|
|
|
|
|
|
|||||
Какие можно сделать выводы?
Если сравнить исходную и главную задачи, можно заметить, что исходная задача имеет 3 ограничения и 2 переменные, а главная – 2 ограничения и 4 переменные. В принципе, уменьшение количества ограничений – это хорошо, так как не раз подчеркивалось, что методы ЛП весьма чувствительны к именно к количеству ограничений.
Но количество переменных возросло. Потребовалось вычислить координаты всех вершин многоугольника, соответствующего диагональному блоку.
145

Рассматриваемый метод декомпозиции7 ориентирован на решение задач очень большой размерности.
Естественно, что для вычисления координат всех вершин требуется нереализуемая мощность ЭВМ. Вулф и Данциг – авторы метода декомпозиции – доказали, что решение главной задачи можно искать не зная ни всех вершин многогранника, определенного диагональным блоком, ни количества этих вершин.
Достаточно знать лишь один (любой) опорный план главной задачи, а также базисную и обратную к ней матрицы соответствующего опорного решения.
При этом (что самое важное в методе) координирующая задача в явном виде нигде не записывается8.
Остановимся на этом методе подробнее.
1.4.6. Обоснование метода декомпозиции Данцига-Вулфа
Итак, представим себе главную задачу:
|
k |
|
|
|
|
|
|
|
|
cl l max |
|
|
|
|
|||||
l 1 |
|
|
|
|
|
|
|
||
|
|
k |
|
|
Здесь cl |
cxl ; |
|||
|
|
Pl |
l P0 |
||||||
|
|
l 1 |
|
|
|
|
|
|
|
|
|
0, |
(l |
|
) |
|
|
|
|
l |
1, k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B0 |
|
|
|
|
|
|
|
P0 |
|
1 |
||||
|
|
|
|
1 |
|
r0 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Axl Pl 1 ;
Пусть:
B – базисная матрица некоторого опорного решения этой задачи; B-1– обратная матрица; Cбаз – вектор коэффициентов ЦФ при
базисных переменных.
В соответствии с вычислительной схемой модифицированного симплекс-метода9 (МСМ) текущее решение является оптималь-
7Непосредственно о декомпозиции речь пока не идет.
8Достаточно представить (мысленно), что эта задача есть (есть не в памяти ЭВМ, а вообще есть!).
9Почему МСМ? Дело в том, что именно в рамках схемы МСМ можно не знать коэффициентов разложения тех векторов, чьи оценки нужно вычислить.
146

ным, если для всех небазисных векторов Pl (l 1,k) оценки этих векторов не отрицательны:
l cбазB 1Pl cl = cбазB 1Pl cxl 0. |
(1.95) |
Начнем анализ этого выражения на предмет исследования возможности его практического использования.
Рассмотрим произведение B 1P : 10 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
матрица |
|
|
|
|
AX l |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
B 1P |
размерностью |
(r 1) |
|
|
|
|
|
|
= |
|
|
|
||
l |
|
|
|
й |
|
|
|
|
|
|
|
(1.96) |
||
|
|
(r0 1) r0 |
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
столбец |
|
|
|
|
|
|
|
|||||
|
|
r столбцов |
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R Axl |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Подставим (1.96) в (1.95): |
|
|
|
|
|
|
|
|
|
|
l |
|||
l Cбаз (R0 Axl V ) Cxl – оценка вектора Pl |
|
|||||||||||||
Ax |
|
|||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l (CбазR0 A C)xl CбазV . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(1.97) |
||||||
Известно, что если решение не оптимальное, вектор Pl, которому соответствует отрицательная оценка (желательно, максимальная по абсолютной величине), должен быть включен в состав базисных векторов.
Проблема же в том, что l нельзя вычислить до тех пор, пока
не известны все элементы вектора Pl |
|
l |
|
Ax |
. |
||
|
|
1 |
|
В свою очередь, численное определение этих элементов невозможно до тех пор, пока не известна соответствующая экстремальная точка x .
То есть нужно сначала определить эту экстремальную точку. А как ее определить, если мы знаем только обратную матрицу
10 B 1 Pl -это вектор коэффициентов разложения вектора Pl по базису.
147
главной задачи B-1 и Сбаз. Сама же задача задана неявно. Ее просто нет!
Идея метода Данцига-Вулфа заключается в том, чтобы заме-
нить поиск отрицательной оценки путем последовательного перебора свободных векторов текущего опорного решения направленным поиском только одной экстремальной точки, которой соответствует минимальная оценка связанного с этой точкой вектора главной задачи.
Если окажется, что найденная таким образом минимальная оценка неотрицательна, задача решена. Точнее, решена главная задача, а следовательно, и исходная.
В противном случае ясно, какой вектор следует вводить в базис: этот вектор будет полностью определен координатами найденной экстремальной точки.
Итак, нужно найти экстремальную точку, которой соответствует вектор главной задачи, имеющий минимальную оценку.
Это можно сделать, решив следующую задачу:
min
DX B x 0.
Здесь следует обратить внимание на то, что индекс номера вершины отсутствует. Этот индекс просто неизвестен, так как соответствующую вершину еще нужно найти.
В качестве переменных этой задачи выступают координаты искомой вершины.
Мы предположили, что множество, определенное ограничениями DX B , x 0, ограничено. Следовательно, минимальное
значение также ограничено и должно соответствовать некоторой экстремальной точке. Ее-то и нужно найти.
Уже было показано (1.97), что:
l (CбазR0 A C)x CбазV.
Теперь, опустив индекс l, имеем: |
|
(CбазR0 A C)X CбазV. |
(1.98) |
Ввиду того, что CбазV – постоянная величина, не зависящая от X , задаче ЛП можно придать следующий вид:
148

z (CбазR0 A C)X min
DX B |
(1.99) |
x 0. |
|
Назовем эту задачу частной (или локальной).
Допустим, мы решили эту задачу11, и z* – оптимальное значение ЦФ. Отсюда узнаем и минимальную оценку:
min z* CбазV
и, что самое главное, и сам свободный вектор, который обладает данной оценкой. Действительно, мы знаем координаты экстре-
мальной точки xl , на которой ЦФ локальной задачи имеет значение z*. Следовательно, можно сформировать вектор главной задачи, соответствующий этой точке:
Axl Pl 1 .
Здесь l – это не номер вершины, а номер итерации, на которой данная вершина найдена.
Теперь, если min z* CбазV 0, то главная задача решена.
Исследуемое на текущей итерации решение – оптимальное. Можно восстановить решение исходной задачи. Делается это следующим образом.
Пусть *– множество номеров базисных переменных главной задачи.
Тогда, по найденным координатам соответствующих экстре-
мальных точек x j (j *) можно восстановить решение исходной задачи:
X опт j x j . j *
11 Другого, в предположении, что допустимое множество ограничено, не может быть.
149

Axl
Если min 0 , то вектор Pl 1 нужно ввести в базис но-
вого опорного решения главной задачи. Делается это по правилам МСМ.
Следует обратить внимание, что используются общие принципы обычного симплекс-метода: последовательный переход от одного опорного решения координирующей задачи к другому, лучшему. Но при каждом таком переходе решается локальная задача для поиска вектора с минимальной оценкой. При этом, на каждой итерации формируется частная ЦФ локальной задачи12.
Смысл метода декомпозиции заключается в том, что при решении локальной задачи:
z (CбазR0 A C)X min DX B
x 0
мы сталкиваемся с чисто диагональной структурой ее матрицы ограничений (без блока-связки).
Система ограничений DX B – это сокращенная запись следующей системы ограничений:
Dj xj |
= B1 |
j 1 |
|
Dj xj |
= B2 |
j 2 |
|
............................................................................................ |
|
Dj x j |
= B |
j
............................................................................................
Dj x j = BL j L
Такая структура допускает простое разделение задачи на L подзадач меньшей размерности. Сборка же решения осуществляется следующим образом.
12 Коэффициенты ЦФ локальной задачи определяются через обратную матрицу очередного опорного решения главной задачи.
150
