
Жолобов Ввведение в Математическое 2008
.pdf
ну: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
Z (t) c |
|
|
(t) X |
|
|
(2 2t , 5 5t |
, 0) 30 |
160 140t . |
||||
|
0 |
|
баз |
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t>1 |
второе неравенство перестает выполняться: оценка |
|||||||||||
вектора A4 |
|
становится отрицательной, т.е. вектор |
A4 |
нужно ввести |
||||||||
в базис. |
|
|
|
|
|
|
|
|
|
|
|
|
Подготовим |
|
|
переход |
к новому |
базису. |
Для этого в |
||||||
табл. 1 (t=0) внесем необходимые изменения. |
|
|
||||||||||
Положим t=1 |
|
и соответственно изменим коэффициенты целе- |
||||||||||
вой функции, |
ее значение, |
используя выражение для целевой функции, |
||||||||||
а также оценки свободных векторов (оценки этих векторов, как функции параметра t известны ).
|
В результате получим первую симплекс-таблицу (t=1) |
для про- |
||||||||
должения решения задачи: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Баз |
Cбаз |
Ao |
-3 |
0 |
10 |
0 |
0 |
0 |
|
|
A2 |
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
|
0 |
5 |
-1/4 |
1 |
0 |
1/2 |
-1/4 |
0 |
|
|
|
A3 |
10 |
30 |
3/2 |
0 |
1 |
0 |
1/2 |
0 |
|
|
A6 |
0 |
10 |
2 |
0 |
0 |
-2 |
1 |
1 |
|
|
Табл.1 |
(t=1) |
300 |
18 |
0 |
0 |
0 |
5 |
0 |
|
|
A4 |
0 |
10 |
-1/2 |
2 |
0 |
1 |
-1/2 |
0 |
|
|
A3 |
10 |
30 |
3/2 |
0 |
1 |
0 |
1/2 |
0 |
|
|
A6 |
0 |
30 |
1 |
4 |
0 |
0 |
0 |
1 |
|
|
Табл.2 |
(t=1) |
300 |
18 |
0 |
0 |
0 |
5 |
0 |
|
Решение задачи представлено двумя симплекс-таблицами. Следует отметить весьма важную особенность приведенного решения.
Во-первых, это оценка вектора A4 в первой таблице. Отрицательный знак при нуле подчеркивает то обстоятельство,
что при любом, сколь угодно малом увеличении параметра t решение становится неоптимальным.
Во-вторых, при переходе ко второй таблице не изменились ни оценки векторов, ни значение целевой функции. Имеет место случай
альтернативного базиса.
Этот случай имеет простую геометрическую интерпретацию: при t=1 линия уровня "ложится" на ребро, соединяющее две смежные вершины допустимого множества, и любой точке этого ребра соответствует одно и то же значение целевой функции (рис.1.23).
171

С'
С
Рис.1.23. Случай альтернативного базиса
Найдем новое критическое значение параметра t такое, что в интервале [t1,t2] решение остается оптимальным. Проделаем это, как и на предыдущей итерации, в три приема:
1. Вычислим вектор-функцию симплексных множителей:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 / 2 |
|
0 |
|
|
5 |
5t |
|
|||||||||||||
(t) c |
(t)B |
1 (0, 5 5t, 0) |
0 |
|
|
|
|
1 / 2 |
|
0 (0, |
, 0); |
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
баз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
2. |
|
Найдем оценки свободных векторов, как функции параметра: |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
5 5t |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
9 27t |
|
|
||||||||||
|
|
(t) (t) A |
c (t) (0, |
|
, 0) |
|
3 |
|
(3 |
|
6t) |
; |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
1 |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
5 5t |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(t) (t) A |
c |
|
(t) (0, |
|
|
, 0) |
|
0 |
|
(2 2t) 2 |
2t; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
5 5t |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
5 5t |
|
|
|
|
|
||||||
|
|
(t) (t) A |
c |
|
(t) (0, |
|
|
, 0) |
|
1 |
|
0 |
|
|
. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
5 |
|
5 |
|
5 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. Найдем критическое значение параметра |
|
t=t2 такое, что в интерва- |
||||||||||||||||||||||||||||||||
ле |
[t1,t2] |
выполняется система неравенств: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
9 27t |
|
0; |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2t |
0; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Очевидно, что при любых |
t 1 эти неравенства будут выпол- |
|||||||||||||||||||||||||||||||
172

няться, следовательно, решение, записанное во второй симплекстаблице, x0=(0,0,30,10,0,30) будет оставаться оптимальным.
В полуоткрытом интервале t 1 значение целевой функции будет изменяться по закону:
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
Z |
|
(t) c |
|
(t) X |
|
(0, 5 5t, 0) 30 |
|
150 |
150t. |
||||||||
|
|
0 |
|
|
баз |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметрический анализ закончен. Его результаты сведем в |
|||||||||||||||||
таблицу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
t |
|
|
Оптимальное решение |
|
|
|
|
|
Z0(t) |
|
|||||||
|
|
|
x1 |
|
x2 |
|
x3 |
x4 |
x5 |
|
|
x6 |
|
|
||||
|
0 t 1 |
|
|
0 |
|
|
5 |
|
|
30 |
0 |
0 |
|
|
10 |
|
160+140t |
|
|
t 1 |
|
|
0 |
|
|
0 |
|
|
30 |
10 |
0 |
|
|
30 |
|
150+150t |
|
Рассмотрим задачу А из предыдущего раздела на конкретном примере. Пусть требуется провести параметрический анализ следующей задачи ЛП.
Пример 1.29
|
2x1 3x2 |
max, |
|
|
||||||
|
|
|
x2 |
x3 |
|
|
|
80, |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
x1 |
2x2 |
x4 |
|
|
|
180, |
||||
3x |
2x |
|
x |
|
|
|
300 t, |
|||
|
1 |
|
|
2 |
|
5 |
|
|
|
|
|
x |
|
|
|
x |
|
80, |
|||
|
1 |
|
|
|
|
|
|
6 |
|
|
|
|
x |
j |
0, j 1, 6. |
||||||
|
|
|
|
|
|
|
|
|
|
|
Принимаем t=0 и решаем задачу симплекс-методом. Решение задачи для приведено в последней симплекс-таблице.
Баз |
Сбаз |
A0 |
2 |
3 |
0 |
0 |
0 |
0 |
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
|
|
|
|
|
|
|
|
A2 |
3 |
60 |
0 |
1 |
0 |
3/4 |
-1/4 |
0 |
A1 |
2 |
60 |
1 |
0 |
0 |
-1/2 |
1/2 |
0 |
A3 |
0 |
20 |
0 |
0 |
1 |
-3/4 |
1/4 |
0 |
A6 |
0 |
20 |
0 |
0 |
0 |
1/2 |
-1/2 |
1 |
Табл |
.4(t=0) |
300 |
0 |
0 |
0 |
5/4 |
1/4 |
0 |
Обратная матрица оптимального решения выделена. Найдем вектор-функцию разложения вектора A0 по базису:
173

|
0 |
3 4 |
1 4 |
0 |
80 |
|
60 t |
4 |
|
|
|
1 2 |
|
|
|
|
|
t |
|
B 1 A |
(t) 0 |
1 2 |
0 |
* 180 |
|
60 |
2 . |
||
0 |
1 |
3 4 |
1 4 |
0 |
300 t |
20 |
t |
4 |
|
|
|||||||||
|
|
1 2 |
1 2 |
|
|
|
|
t |
|
|
0 |
1 |
80 |
|
20 |
2 |
|||
Решим систему неравенств: |
|
|
|
60 t |
4 |
0, |
|
|
t |
2 |
0, |
60 |
|||
|
t |
|
0, |
20 |
4 |
||
|
t |
2 |
0. |
20 |
|||
Отсюда находим первое критическое значение параметра t=t1 такое, что в интервале [0, t1] решение остается допустимым.
При t>40 последнее неравенство не выполняется, следовательно, t1=40. В интервале [0,40] закон изменения оптимального значения целевой функции определяется следующим образом:
60 t 4
4
Z0(t) = cбаз X0 (t) =(3,2,0,0) 60 t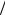 2 =3*(60 - t/4) + 2*(60+t/2) =
2 =3*(60 - t/4) + 2*(60+t/2) =
20 t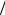 420 t
420 t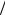 2
2
=300+t/4 .
Заменим в оптимальной симплекс-таблице столбец A0.
Для этого при t=t1=40 пересчитываем столбец A0 последней симплекс-таблицы:
60 t |
4 |
|
|
|
50 |
|
60 t |
2 |
|
|
= |
80 |
|
20 t |
4 |
|
|
|
30 |
|
20 t |
2 |
|
t 40 |
|
0 |
|
|
|
|
Вычислим новое значение целевой функции:
Z(t=40) = 300+10 = 310.
Переписываем последнюю симплекс-таблицу с новыми значениями коэффициентов столбца A0 .
При t>40 четвертая координата в разложении вектора A0 становится отрицательной, поэтому для поиска оптимального решения задачи используется двойственный симплекс-метод.
174

Баз |
Сбаз |
A0 |
2 |
3 |
0 |
0 |
0 |
0 |
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A2 |
3 |
50 |
0 |
1 |
0 |
3/4 |
-1/4 |
0 |
A1 |
2 |
80 |
1 |
0 |
0 |
-1/2 |
1/2 |
0 |
A3 |
0 |
30 |
0 |
0 |
1 |
-3/4 |
1/4 |
0 |
A6 |
0 |
-0 |
0 |
0 |
0 |
1/2 |
-1/2 |
1 |
t=40 |
|
310 |
0 |
0 |
0 |
5/4 |
1/4 |
0 |
|
|
|
|
|
|
|
|
|
A2 |
3 |
50 |
0 |
1 |
0 |
1/2 |
0 |
-1/2 |
A1 |
2 |
80 |
1 |
0 |
0 |
0 |
0 |
1 |
A3 |
0 |
30 |
0 |
0 |
1 |
-1/2 |
0 |
1/2 |
A5 |
0 |
0 |
0 |
0 |
0 |
-1 |
1 |
-2 |
t=40 |
|
310 |
0 |
0 |
0 |
3/2 |
0 |
1/2 |
|
|
|
Решение задачи при t=40. |
|
|
|||
Найдем второе критическое значение параметра t=t2 такое, что в интервале [40,t2] полученное решение остается допустимым и оптимальным:
|
0 |
1 2 |
0 |
1 2 |
80 |
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
B 1 * A (t) 0 |
0 |
0 |
1 |
* 180 |
|
|
80 |
. |
|
0 |
1 |
1 2 |
0 |
1 2 |
300 t |
|
30 |
|
|
|
|||||||||
|
|
1 1 |
|
|
|
|
|
|
|
|
0 |
2 |
80 |
|
40 t |
||||
Очевидно, что при всех t > 40 решение будет оставаться допустимым и оптимальным. При этом целевая функция будет иметь постоянное значение: Z(t)=310.
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
Z0 (t) (3, 2, 0, 0) |
|
3 * 50 2 * 80 150 160 310. |
||||||||
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 t |
|
|
|
|
|
|||
Параметрический анализ закончен. Сведем его результаты в таб- |
||||||||||
лицу: |
|
|
|
|
|
|
|
|
|
|
|
|
Оптимальное решение |
|
|
||||||
Интервал |
x1 |
x2 |
|
|
x3 |
|
x4 |
x5 |
x6 |
Z(t) |
0 t 40 |
60+t/2 |
60-t/4 |
|
20+t/4 |
0 |
0 |
20-t/2 |
300+t/4 |
||
|
|
|
|
|
|
|
|
|
|
|
t > 40 |
80 |
50 |
|
|
30 |
|
0 |
-40+t |
0 |
310 |
|
|
|
|
|
|
|
|
|
|
|
175
150
140
130
120
110
100
90
80
70
60
50
40
30
20
10
0
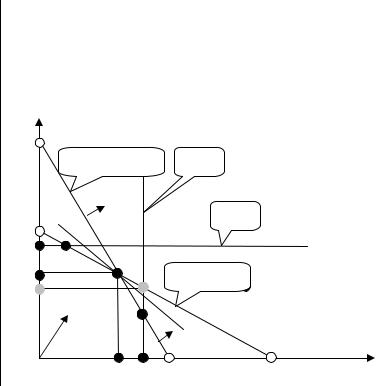
Графическая иллюстрация |
|
|||
2x1 + 3x2 |
max, |
|
|
|
x2 80, |
огр.1 |
|
|
|
x1 |
+ 2x2 |
180, |
огр.2 |
|
3x1 |
+ 2x2 300+t, |
огр.3 |
|
|
x1 |
|
80, |
огр.4 |
|
x1, x2 0. |
|
|
||
|
3x1 |
+ 2x2 300+t |
x1 80 |
|
x2 80
x1 + 2x2 180
| | | | | | | | | | | | | | | | | | | | |
60 |
80 |
100 |
180 |
1.4.11.Проблемы накопления ошибок в симплекс-методе
Взаключение этого раздела скажем несколько слов об основных проблемах реализации симплекс-метода.
Различные варианты МСМ отличаются, в основном, оптимизацией за счет разреженности матриц. При этом достигается не только уменьшение необходимого объема памяти, но и повышение скорости вычислений.
Значение последнего фактора не ограничивается только тем, что сокращается время решения задач ЛП.
Дело в том, что сокращение объема вычислений обеспечивает большую эффективность и в плане численной устойчивости решений.
Проблема устойчивости, связанная с накоплением ошибок, пожалуй, самая острая в симплекс-методе.
176
Если число итераций велико по сравнению с m, базисная матрица должна периодически обращаться заново. Необходимость пересчета обратной базисной матрицы возникает тогда, когда устанавливается факт ухудшения точности. Здесь используются специальные приемы.
Например, можно вычислить оценку любого базисного вектора – она должна быть нулевой. Можно вычислить разложение любого базисного вектора – должен получиться единичный вектор.
Контрольные вопросы и задачи к разделу 1.4
1.Составьте схему алгоритма модифицированного симплексметода, сопряженного с методом М-задачи для поиска исходного опорного решения.
2.Проанализируйте случай неограниченности целевой функции на допустимом множестве в методе декомпозиции Данцига-Вулфа. Каким образом возникновение этого случая должно обрабатываться в вычислительной схеме алгоритма?
3.Предложите действия при параметрическом анализе, если в мо-
мент времени t0 при решении задачи срабатывает признак неограниченности целевой функции.
4.Предложите действия при параметрическом анализе, если в мо-
мент времени t0 невозможно найти ни одного допустимого решения.
5.Возможен ли одновременный параметрический анализ коэффициентов целевой функции и правых частей системы ограничений?
6.Решить задачу модифицированным симплекс-методом
9x1 10x2 max
3x1 4x2 109
4x1 4x2 124 x1 19
x2 19
x1,2 0.
177

7. Дана задача ЛП:
-100x1 -260x2 -280x3 -110x4 max
x1 |
+2x2 |
+x3 |
-x5 = 1 |
x2 |
+2x3 |
+x4 |
-x6 = 4 |
xj 0 (j=1 6).
На очередном шаге решения этой задачи МСМ получена таб-
лица: |
|
|
|
|
|
|
|
|
|
|
|
Баз |
Сбаз |
|
|
А0 |
E1 |
|
E2 |
|
|
|
A3 |
-280 |
|
|
1 |
1 |
|
0 |
|
|
|
A4 |
-110 |
|
|
2 |
-2 |
|
1 |
|
|
|
Tабл.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти оптимальное решение этой и двойственной к ней зада- |
||||||||||
чи. |
|
|
|
|
|
|
|
|
|
|
8. Решить задачу методом декомпозиции Данцига-Вулфа: |
||||||||||
|
|
x1 |
2x2 |
|
3x3 |
x4 |
max |
|||
|
|
2x1 |
3x2 |
|
3x3 |
3x4 |
5 |
|||
|
|
x1 |
x2 |
|
|
|
3 |
|||
|
|
x1 |
2x2 |
|
|
|
1 |
|||
|
|
|
|
|
|
x3 |
2x4 |
2 |
||
|
|
|
|
|
|
2x3 |
x4 |
5 |
||
|
|
xj 0( j 1..4). |
|
|
|
|
||||
9. Дана задача ЛП: |
2x1 - 4x2-3x3+x4 max, |
|
|
|
||||||
|
|
|
|
|
||||||
|
|
x1 - 3x2+x3 |
= 5, |
|
|
|
||||
|
|
2x1 - 2x2 |
|
+ x4= 20 |
|
|
|
|||
|
|
|
xj 0, |
(j=1 4). |
|
|
|
|
||
Определить зависимость оптимального решения задачи от коэффициента c3 целевой функции.
178
10. Дана задача ЛП:
2x1 |
- 4x2-3x3+x4 max, |
|
x1 |
- 3x2+x3 |
= 5, |
2x1 |
- 2x2 |
+ x4= 20 |
xj 0, (j=1 4).
Определить зависимость оптимального решения задачи от коэффициента a1 целевой функции.
1.5. Дробно-линейное программирование
Рассмотрим следующую прикладную задачу. Для выполнения n различных работ могут быть использованы рабочие m квалификационных групп.
При выполнении i-й группой рабочих j-й работы выработка в единицу времени составляет cij единиц ( i=1 m; j=1 n ).
Общий фонд времени, в течение которого i-я группа рабочих может быть занята выполнением работ, не превышает bi единиц времени, а j-я работа должна быть выполнена в объеме не менее
aj единиц.
Необходимо составить такой план выполнения работ, который обеспечивает максимальную производительность.
Производительность= |
объем работ |
. |
||
затраты времени |
||||
|
|
|
||
Построим модель. Пусть xij |
– время, затрачиваемое i-й группой |
|||
рабочих для выполнения j-й работы (i=1 m; j=1 n). |
|
|||
Тогда при плане { xij } |
общий объем работ (Z1) составит: |
|||
|
m |
n |
|
|
|
Z1= cij xij . |
|
||
|
i 1 j 1 |
|
||
Общие затраты времени (Z2) на выполнение этого объема ра- |
||||
бот определяются следующим образом: |
|
|||
|
m |
n |
|
|
|
Z2= xij . |
|
||
|
i 1 |
j 1 |
|
|
При плане { xij } общая производительность всех работ составит:
179
|
|
m |
n |
|
Z |
|
cij xij |
||
|
i 1 |
j 1 |
||
1 |
|
|
. |
|
Z2 |
m |
n |
||
|
xij |
|||
|
|
i 1 |
j 1 |
|
Сформулируем ограничения задачи.
j-я работа должна быть выполнена в объеме не менее aj единиц. Следовательно, должно иметь место:
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cij xij |
aj |
( j |
|
|
|
|
) . |
||||||||
|
1,n |
||||||||||||||||
i-я |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
группа рабочих может быть занята выполнением работ не |
|||||||||||||||||
более bi |
единиц времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xij |
bi |
(i |
1, m |
). |
|
||||||||||
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Последнее, естественное, ограничение – это требование неот- |
|||||||||||||||||
рицательности переменных: |
xij 0 ( i=1 m; j=1 n ). |
||||||||||||||||
Окончательно модель приобретает вид: |
|||||||||||||||||
|
|
|
|
|
m |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
cij xij |
|||||||||||||
|
|
|
i 1 |
j 1 |
|
max |
|||||||||||
|
|
1 |
|
|
|
|
|||||||||||
|
Z2 |
m |
n |
|
|||||||||||||
|
|
|
xij |
||||||||||||||
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cij xij |
aj , |
( j |
1,n |
) |
|||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xij bi , |
(i |
1, m |
) |
||||||||||||
j 1
xij 0, ( i=1 m; j=1 n ).
В практике планирования с использованием математических моделей оптимизационных задач подобные нелинейные задачи встречаются довольно часто. Они составляют целый класс задач математического программирования – класс задач дробно-
линейного (ДЛП) или гиперболического программирования. В об-
щей постановке задача ДЛП имеет вид:
180
