Жолобов Ввведение в Математическое 2008

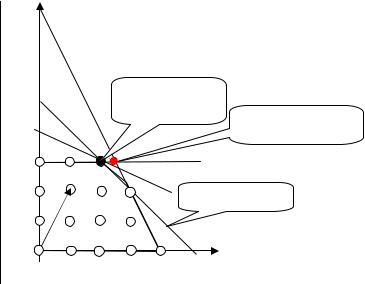
x1+2x2 max

Рис.2.19. Геометрическая интерпретация правильного отсечения

Перед тем, как закончить изложение метода отсечения, остановимся на некоторых проблемах, связанных с использованием этого метода.

2.3.5.Проблемы первого алгоритма Гомори

Впредставленной редакции алгоритма, по мере увеличения количества задач, растет и размерность этих задач. Действительно, на каждой большой итерации в состав базисных переменных вводится новая дополнительная переменная и соответственно новое ограничение.

При этом количество свободных переменных не изменяется.

Так, размерность последней задачи (m+k) (n+k), где (m+k) – количество строк,

(n+k) – количество столбцов.

По сути дела, все зависит от количества итераций, а оно может быть очень большим.

Гомори предложил и обосновал следующий прием уменьшения размерности.

Если при решении задачи ЛП(r) в базис оптимального решения войдет некоторая переменная xn+k+1 (k < r), то соответствующая строка и столбец просто вычеркиваются из симплекс-таблицы.

281

Таким образом, в самом худшем случае в базис войдут все векторы исходной задачи, а их n. Количество же свободных переменных – одно и то же (n-m). Следовательно, в худшем случае размерность задачи составит:

n (n+(n-m))=n (2n-m).

Есть в этом алгоритме и другие проблемы, на которых следует остановиться.

Ошибки округления. Эти ошибки, возникающие в процессе вычислений, могут приводить к получению неверного решения.

В процессе реализации алгоритма все промежуточные решения – оптимальные решения ЛП(k)-задач – не являются допустимыми решениями исходной ЛЦП-задачи. Это не позволяет получить промежуточное целочисленное решение, отличное от оптимального, что делает проблематичным использование этого алгоритма для приближенного решения задач ЛЦП.

Наконец, последнюю проблему рассмотрим на примере.

Пример 2.16

Решаем задачу с помощью алгоритма Гомори:

282

При работе по ДСМ срабатывает признак недопустимости. Проблема заключается в том, что 1-й алгоритм Гомори предпола-

гает целочисленность всех переменных, в том числе и дополнительных. Поэтому достаточным условием правильной работы этого алгоритма является целочисленность всех параметров задачи.

Правильное решение

283

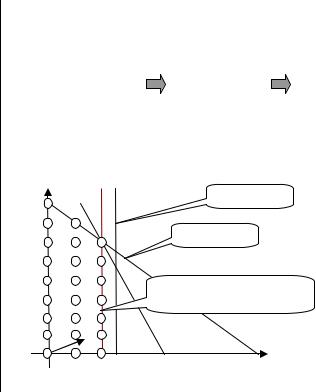
Получено оптимальное целочисленное решение. Геометрическая интерпретация приведена на рис. 2.20.

Рис. 2.20. Геометрическая интерпретация правильного отсечения

Контрольные вопросы и задачи к разделу 2.3

1.Дайте определение выпуклой линейной оболочки допустимого множества задачи ЛЦП.

2.Чем отличается выпуклая линейная оболочка множества от самого множества?

3.Назовите основные требования, которым должно отвечать правильное отсечение.

4.Выпишите уравнение правильного отсечения в первом алгоритме Гомори.

5.Какие особенности возникают при решении с помощью первого алгоритма Гомори задач с допустимым множеством, представленным в виде нестрогих неравенств?

6.Изобразите допустимое множество задачи линейного целочисленного программирования на графике. Нарисуйте границы выпук-

284

лой линейной оболочки допустимого множества. Получите аналитическое представление выпуклой линейной оболочки.

x1 2x2 max x1 4x2 21.5 2x1 11

2x2 9

x1, x2 0, целые

7. Дана задача линейного целочисленного программирования: x1 2x2 max

2x1 x2 13

x1 2x2 5 x1 5

x2 4

x1, x2 0, целые

Исходя из определения, проверьте, являются ли следующие отсечения правильными:

а) x1 x2 2

б) x1 2x2 11

в) x1 x2 8

8. Решите задачу ЛЦП с помощью первого алгоритма Гомори x1 10x2 max

x1 8x2 28 x1 4

x1, x2 0, целые

9. Решите задачу ЛЦП с помощью первого алгоритма Гомори

x1 x2 max8x1 15x2 15 x1 7.5

x1, x2 0, целые

285

2.4. Метод ветвей и границ

Среди методов, ориентированных на точное и /или приближенное решение задач комбинаторного типа, особое место занимает группа методов, объединенных по общим названием "Метод ветвей и границ" (МВиГ).

Различные реализации МВиГ объединяет общая идея – идея замены полного перебора направленным, эвристическим поиском допустимых решений (комбинаций). Эффект достигается за счет массового отсеивания так называемых "бесперспективных" вариантов.

В основу различных модификаций МВиГ положено несколько принципов, которые рассматриваются в следующем разделе

2.4.1. Принципы метода ветвей и границ

Вычисление верхней или нижней границы (оценки) ЦФ на допустимом множестве или некотором его подмножестве;

Последовательное разбиение допустимого множества (ветвление), шаг за шагом сокращающее допустимое множество;

Пересчет оценок (границ);

Установление признака оптимальности;

Оценка точности приближенного решения.

Вычисление границы

Для определенности рассмотрим в самой общей постановке задачу комбинаторного типа на минимум ЦФ:

F(x) min

x G.

Здесь G – множество допустимых решений (комбинаций); x – элемент множества G.

Иногда удается найти нижнюю границу (оценку) целевой функции F на G или на некотором его подмножестве G' G.

Нижняя граница – это такое число (G) (или (G')), что дляx G имеет место F(x) (G). Способ вычисления нижней границы существенно зависит от содержательной постановки задачи.

Например, в задаче поиска самого короткого маршрута из некоторой точки A в точку B с учетом существующей транспортной

286

сети в качестве нижней границы можно взять евклидово расстояние между этими точками (короче пути нет и не может быть).

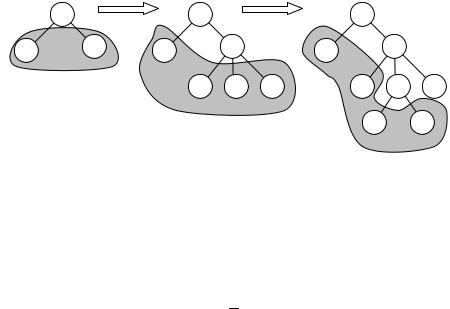
Ветвление

Реализация метода ветвей и границ связана с постепенным разбиением допустимого множества G на подмножества меньшей мощности – с представлением этого подмножества в виде дерева подмножеств. Принцип, по которому осуществляется разбиение, также зависит от конкретной задачи (рис. 2.21).

Рис.2.21. Ветвление задачи

Пересчет оценок

Пересчет оценок основан на очевидном факте. Если G1 G2, то должно иметь место

Учитывая это обстоятельство, предполагается, что если разбить некоторое множество G' G на подмножества

G'1, G'2,…, G's, причем G'= G'i , то оценка любого подмно-

i 1,s

жества должна быть не меньше оценки подмножества G':

Таким образом, после разбиения любого подмножества, необходимо вычислить оценки всех вновь образованных подмножеств – уточнить оценки.

Пусть далее имеет место следующее соотношение: 287

F (x ) (Gν ) min{ (Gi )} .

i 1,s

Тогда x – оптимальное решение задачи. Доказательство вытекает непосредственно из определения границы.

Оценка точности приближенного решения

Пусть G= Gi , и min{ (Gi )}.

i 1,s

Пусть далее известно некоторое допустимое решениеx Gi .

В соответствии с определением границы должно иметь место следующее соотношение:

min F(x) F(x) .

x G

Если разность F(x) невелика, т.е. не превышает некоторого порогового значения, выбранного для данной задачи, то x

можно принять в качестве приближенного решения задачи, а использовать для оценки точности решения.

Можно задаться и относительной погрешностью (%). В этом случае x принимается в качестве приближенного решения задачи, если имеет место:

F (x) 100% ε.

2.4.2. Общая схема метода ветвей и границ

Дана задача

F(x) min,

x G.

Введем понятие рекорда, имеющее принципиально важное значение в методе ветвей и границ.

Рекордом R= F(x') будем называть наименьшее из известных на конкретный момент времени значение, которое принимает ЦФ

на некотором допустимом решении x' G.

Шаг 1. Заносим множество G в предварительно очищенный список задач S: S={G}. Полагаем R= M, где M – достаточно большое положительное число.

Шаг 2. Для каждого подмножества списка вычисляем нижние границы (оценки). При этом оценки вычисляются только для тех подмножеств, для которых они не вычислялись ранее.

288

Шаг 3. Последовательно анализируются подмножества списка и вычисленные для этих подмножеств оценки в порядке неубывания оценок.

Пусть рассматривается очередное подмножество списка G*. Если G*= , это подмножество удаляется из списка.

Если (G*) R, то G* также удаляется из списка (как "бесперспективное").

Если G* – одноэлементное подмножество, или удается установить, что на некотором решении x* G* имеет место(G*)=F(x*)<R, фиксируется новый рекорд: R= F(x*).

В результате список "очищается" от всех бесперспективных подмножеств.

Шаг 4. Если список пустой21 (S= ), то конец – задача не имеет решения.

Шаг 5. Из списка выбирается подмножество с минимальной оценкой. После выполнения процедуры на шаге 3 – это первое в списке подмножество. Обозначим его Gmin.

Если Gmin – одноэлементное подмножество, или удается установить, что на некотором решении Xmin Gmin имеет место

(Gmin)=F(Xmin), то получено оптимальное решение. Конец.

Шаг 6. По заранее установленному признаку подмножество Gmin разбивается на ряд новых подмножеств. Эти подмножества заносятся в список S, после чего выполняется шаг 2.

Итак, в процессе работы по алгоритму метода ветвей и границ разбиению подлежат подмножества с минимальной оценкой.

Важно то обстоятельство, что оставшиеся в списке подмножества не отбрасываются (если, конечно, они не признаются бесперспективными). С чем это связано?

Дело в том, что нижняя граница может оказаться недостижимой: просто не существует такого решения, на котором значение ЦФ совпадает с нижней границей, а вычисление достижимой границы весьма трудно реализовать.

21 Поскольку рекорд в данной редакции алгоритма хранится в списке задач, пустой список означает отсутствие решений. Существуют иные редакции алгоритма, в которых рекорд регистрируется отдельно от списка – в этом случае на этом шаге признак отсутствия допустимых решений срабатывать не будет.

289