
Жолобов Ввведение в Математическое 2008
.pdf
Пример 2.29
Задан граф планирования.
|
|
|
X |
|
|
|
ЦЕЛЬ 1 |
|
|
|
ЦЕЛЬ 2 |
|
X11 |
|
X12 X13 |
X14 |
X15 |
X21 |
X22 |
X23 |
X24 |
X25 |
X26 X27 |
1. Главная цель может быть достигнута, если будет достигнута ЦЕЛЬ1 и ЦЕЛЬ2.
2. ЦЕЛЬ1 можно достичь, только решив одну из задач X11 или X12.
3. ЦЕЛЬ2 можно достичь, только решив одну из трех задач X13, или
X14, или X15
4. Для решения задачи X11 необходимо решить задачу X21 и задачу X22 . 5. Для решения задачи X12 необходимо решить задачу X23 и задачу X24. 6. Для решения задачи X15 необходимо решить все три задачи X25, X26 и
X27.
7. Кроме того, есть еще дополнительное ограничение: задачу X14 можно решить только при условии, что задача X24 решена.
Необходимо сформулировать систему ограничений, при помощи которых можно смоделировать перечисленные логические связи. Решение.
В данном случае можно предложить целый ряд вариантов. Рассмотрим один из них.
Одна из двух задач X11 или X12 должна быть обязательно решена:
X11 + X12 = 1.
Одна из трех задач X13 , X14 или X15 должна быть обязательно решена:
X13 + X14 + X15 = 1.
Для решения задачи X11 необходимо решить задачу X21 и задачу X22:
X21 + X22 2X11.
Для решения задачи X12 необходимо решить задачу X23 и задачу X24:
X23 + X24 2X12.
Для решения задачи X15 необходимо решить все три задачи X25,
X26 и X27:
X25+ X26 +X27 2X15.
Наконец, дополнительное ограничение: задачу X14 можно решить только при условии, что задача X24 решена:
X24 X14.
341
Контрольные вопросы и задачи к разделу 2.6
1.Сформулируйте признак пустого подмножества в задаче булева программирования.
2.Чем отличаются основная и стандартная формы задач булева программирования?
3.Сравните метод плотного заполнения с полным перебором всех комбинаций булевых переменных.
4.Зачем в методе Фора и Мальгранжа наложено требование целочисленности коэффициентов целевой функции?
5.В чем заключается процесс расширения частичного решения в аддитивном алгоритме?
6.Постройте стандартную форму задачи булева программирования:
x1 x2 2x3 x4 max x1 2x2 x3 5
x1 x2 2x3 3x4 3 x1 3x2 x3 4x4 2 x1 , x2 , x3 , x4 0,1
7. Получите допустимое решение задачи булева программирования методом плотного заполнения:
x1 2x2 3x3 max x1 2x2 x3 2
x1 x2 x3 2
x1 x2 x3 0 x1 , x2 , x3 0,1
8. Решите задачу булева программирования методом Фора и Мальгранжа:
2x1 x2 x3 max x1 x2 1
x1 x2 x3 1 x1, x2 , x3 0,1 342
8. Решите задачу булева программирования аддитивным методом: x1 2x2 x3 x4 max
2x1 x2 x3 x4 0x1 x2 x3 x4 1 x1 , x2 , x3 , x4 0,1
10. При проектировании систем автоматической защиты ядерного реактора допускается использовать 4 разновидности автоматиче-
ских устройств реагирования Уj (установлено может быть не бо-
лее одного устройства каждого вида). Каждое устройство обладает весом mj . Конструкция активной зоны не допускает установку за-
щитных устройств с общим весом, превышающим M. Установка устройства вида j обойдется в cj рублей. Необходимо определить
перечень устройств, включаемых в проект, обеспечивающий проекту минимальные затраты по данной статье, при соблюдении следующих требований:
1.Из соображений надежности должно быть установлено не менее трех защитных устройств;
2.Совместное использование устройств У1 и У2 исключает возможность использование устройства У3 ; 3.Использование устройства У4 возможно только при использовании устройства У2 .
2.7 Динамическое программирование
2.7.1.Общие принципы задач динамического
программирования
Динамическое программирование является методом решения оптимизационных задач, основанным на декомпозиции самого вычислительного алгоритма. Основным принципом динамического программирования является разбиение процесса решения задачи на группу последовательных этапов, связанных между собой однонаправленным потоком данных (от предыдущего этапа к последую-
343
щему). В настоящее время методы динамического программирования получили широкое распространение в большом количестве прикладных областей, начиная математическими задачами анализа графов и заканчивая оптимизацией инвестиционных затрат и теорией управления запасами. Интерес к динамическому программированию обусловлен такими его качествами, как абстрактность и фундаментальность идеи, позволяющая применять их в широких масштабах, а также потенциальная возможность снижения вычислительной сложности решаемых задач за счет их декомпозиции. С другой стороны, при реализации алгоритма динамического программирования для конкретной задачи, необходимо провести её серьезный анализ, и обосновать для неё основные принципы, что является трудной неформализуемой задачей. Зачастую конкретная реализация алгоритма весьма сложна для понимания. Как уже говорилось, метод динамического программирования является абстрактным, подобно методу ветвей и границ. Это означает, что суть самого метода составляет набор основных абстрактных принципов, которые необходимо формализовать для решения конкретной задачи. Рассмотрим эти принципы.
Пусть существует некоторая задача, решаемая с помощью динамического программирования. Процесс решения этой задачи должен быть разбит на последовательные этапы. Состоянием системы xi на этапе i будем называть некоторый набор данных, получаемый в процессе работы этапа i. Можно выделить основные принципы методов динамического программирования:
Последовательность этапов – все этапы выполняются друг за другом в жестко заданной последовательности;
Передача состояния от текущего этапа к последующему – генерируемое в процессе работы этапа i состояние передается этапу i+1;
Рекуррентная природа вычислений. Каждый этап i представляет собой некоторую функцию, которая получает на вход вектор со-
стояния предыдущего этапа xi-1, по определенному правилу выделяет некоторые альтернативы, выбирает из них лучшие и формирует новое состояние xi:
xi (xi 1 ) ;
344
Принцип оптимальности Беллмана. Оптимальная стратегия на каждом отдельном этапе определяется исключительно на основании текущего состояния, независимо от состояний и оптимальных стратегий на предшествующих этапах.
Указанные принципы можно понимать достаточно широко. Фактически, любой итерационный алгоритм может быть истрактован как метод динамического программирования. Основным признаком правильного подхода к формализации принципов является низкая степень роста объема данных, образующих состояние системы на последующих этапах. Как и метод ветвей и границ, метод динамического программирования должен сужать количество рассматриваемых альтернатив с полного количества комбинаций (полный перебор) до некоторого допустимого, которое делает возможным (реалистичным) применение современных вычислительных средств (направленный перебор). Без обретения этого качества метод динамического программирования, применяемый на NP- полной задаче, ничем не отличается от полного перебора, что делает невозможным его применение на задачах больших размерностей. Для его обеспечения и введены принципы рекуррентности и оптимальности. Принцип рекуррентности ограничивает информацию, которую может использовать вычислительный процесс на некотором этапе той, которая хранится в состоянии системы. Однако само понятие состояния системы тождественно понятию информации в широком смысле, что позволяет, например, хранить в состоянии системы на шаге k состояния на всех предыдущих шагах
(x1,…xk-1). Для наложения ограничений на понятие состояния системы введен принцип оптимальности, который декларирует независимость оптимизационной стратегии на шаге k от стратегий на предыдущих шагах. Косвенно это приводит к невозможности экспоненциального роста состояния системы, поскольку в последнем случае это означало бы зависимость стратегии на шаге k от альтернатив, рассмотренных на предыдущих шагах.
Итак, для решения конкретной задачи методами динамического программирования, необходимо ответить на следующие вопросы:
Что будет пониматься под отдельным этапом решения задачи?
Какие альтернативы возникают на каждом этапе решения?
345
Как вычислять числовую меру для альтернатив, на основании которой эти альтернативы сравниваются между собой?
Какая информация должна образовывать состояние xi на шаге i?
Каков принцип остановки алгоритма, и существует ли он вообще?
Ответив на эти вопросы, можно работать по следующей обобщенной схеме динамического программирования.
Шаг 1. Положить k=1.
Шаг 2. Выполняется k-й этап решения задачи. На основании со-
стояния предыдущего этапа xk-1 определить альтернативы, вычислить меру альтернатив. С помощью меры отбросить худшие альтернативы. На основании лучших альтернатив сформировать новое
состояние системы xk.
Шаг 3. Если срабатывает признак остановки алгоритма (например, текущий этап – последний), то из состояния системы на последнем этапе извлекается оптимальное решение задачи. В противном случае положить k=k+1 и выполнить шаг 2.
2.7.2.Задача поиска кратчайшего маршрута в графе
Простейшим примером задачи, которую можно решить с помощью динамического программирования, является задача определения кратчайшего пути в графе прямого распространения.
Пусть задан взвешенный ориентированный граф G со специальной структурой. Каждой вершине графа поставлен в соответствие слой – натуральное число от 1 до N. Вершина не может относиться к двум слоям одновременно, равно как и не может быть вершин, не относящихся к какому-либо слою. Дуги в графе существуют только между вершинами двух соседних слоев, причем направление дуги соответствует переходу от вершины с меньшим номером слоя к вершине с большим номером. Первый и последний слои графа содержат ровно одну вершину. Необходимо найти кратчайший маршрут в графе, начинающийся с вершины на первом слое и заканчивающийся вершиной на последнем.
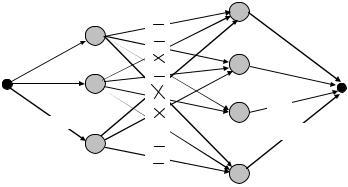
Заданная структура графа определяется требованием отсутствия дуг обратной связи, чтобы в задаче не существовало маршрутов бесконечной длины (циклов). Любой граф, удовлетворяющий этому требованию, может быть преобразован в граф с заданной структурой. Пусть на слое i графа G находится mi вершин
346
ri |
, j 1..m ,i 1..N . Пусть также вес дуги, соединяющей вершины |
|||||||||||||||
j |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ri |
и ri 1 |
, равен |
ci |
j |
(рис. 2.33). |
|
|
|
|
|
||||||
j |
j |
|
|
j |
|
|
|
|
|
|
|
|
|
|
||
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с11N-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c21N-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c11N |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
с111 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
c21N |
|||
|
|
|
|
|
с121 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
 ck1N с1т11
ck1N с1т11  cmN-11N
cmN-11N
Рис.2.33. Граф прямого распространения сигнала
Произведем формализацию необходимых для применения динамического программирования принципов:
1.Этапом решения задачи k будем считать процедуру анализа дуг между слоями k и k+1.
2.Альтернативами на этапе k являются дуги между слоями k и k+1.
3.Состояние системы на первом этапе представляет собой вектор
x1 (s1(1) ,..., sm(1)2 ) , где s(1)j – дуга из начальной вершины в вершину j
второго слоя. Элементы вектора состояния системы на этапе k определяется по следующему принципу. Для каждой вершины rlk 1
из всех альтернативных дуг, в неё входящих, выбирается такая вершина rt k , чтобы выполнялось условие:
f t (x |
k 1 |
) ck |
min ( f j (x |
k 1 |
) ck |
) |
|
tl |
j 1..mk |
jl |
|
||
|
|
|
|
|
|
где f j (x |
) |
s(k ) |
– длина маршрута s(k ) . С точки зрения принци- |
|||
k 1 |
|
j |
|
j |
|
|
пов динамического |
программирования, величина f j (x |
) ck |
и |
|||
|
|
|
|
k 1 |
jl |
|
есть та самая числовая мера, с помощью которой выбирается альтернатива (в данном случае – с помощью минимизации этой меры).
347
Элемент sl( k ) вектора состояния xk, представляющий собой кратчайший маршрут из начальной вершины в вершину rlk 1 , получается добавлением к маршруту st( k 1) дуги из вершины rt k в вершину rlk 1 .
Таким образом, алгоритм динамического программирования может быть упрощенно записан:
Шаг 1. Положить k=1, сформировать вектор x1 (s1(1) ,..., sm(1)2 ) . Значение целевых функций f j (x1 ) c11j . Увеличить k на 1.
Шаг 2. Имеется вектор xk 1 (s1(k 1) ,..., sm(kk 1) ) . Каждый элемент этого вектора s(jk 1) представляет собой кратчайший маршрут из начальной вершины в вершину rjk . Если k=N, то конец – получен самый
короткий маршрут. Его длина записана в единственном элементе вектора xk.
Шаг 3. Сформировать новый вектор состояния xk s1(k ) ,..., sm(kk)1 .
Для каждой вершины r k 1 |
слоя k+1 определить соответствующий |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элемент sl( k ) |
вектора состояния xk. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Шаг 4. |
Для |
каждой |
вершины r k 1 вычислить |
значение |
целевой |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
функции |
f l (x ) |
|
s(k ) |
|
|
. Перейти к шагу 2. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
k |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2.30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
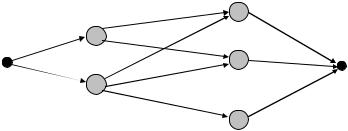
|
Задан граф: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r13 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r12 |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
r1 |
1 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r14 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2 |
|
|
|
r22 |
|
8 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r33 |
|
|
|
|
|
|
|
|
|
|
|
Найти кратчайший маршрут из вершины r 1 |
в вершину r 4 . |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
348 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
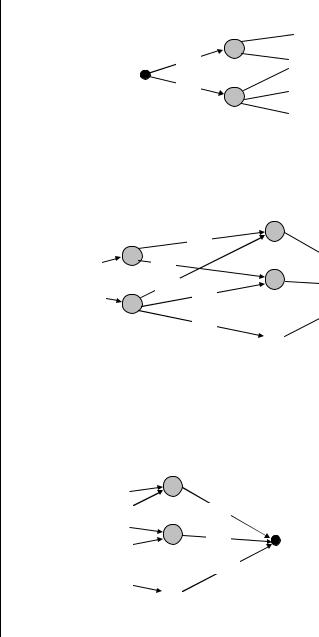
ЭТАП 1
|
r12 |
r11 |
3 |
|
2 |
|
r22 |
Формируем вектор состояния x1 (s1(1) , s2(1) ) . Его элементы:
s1(1) r11 r12 , f 1 (x1 ) 3
s2(1) r11 r22 , f 2 (x1 ) 2
ЭТАП 2
|
r13 |
r12 |
7 |
9 |
r23 |
11
8
r22
9
r33
Формируем вектор состояний x2 (s1( 2 ) , s2( 2 ) , s3( 2 ) ) : min(3 7, 2 11) 10 s1( 2 ) r11 r12 r13 , f 1 (x2 ) 10 min(3 9, 2 8) 10 s2( 2 ) r11 r22 r23 , f 2 (x2 ) 10
min(2 9) 11 s3( 2 ) r11 r22 r33 , f 3 (x2 ) 11
ЭТАП 3
r13
r23 |
7 |
r14 |
6
7
r33
349

Формируем вектор состояний x3 (s1( 3 ) ) :
min(10 7,10 6,11 7) 16 s1( 3 ) r11 r22 r23 r14 , f 1 ( x3 ) 16 .
Мы оказались в конечной вершине, поэтому получено оптимальное решение задачи: получен кратчайший маршрут r11 r22 r23 r14 , длина которого равна 16.
2.7.3. Прямой и обратный ход в задаче динамического программирования
Метод, приведенный выше, работает в прямом направлении: каждый этап добавляет к решению задачи свой фрагмент, и на последнем этапе получается окончательное оптимальное решение. Такой метод получил название алгоритма прямого хода. Однако поскольку этапы вычислений в динамическом программировании выполняются независимо друг от друга и связаны друг с другом только входными и выходными данными, можно формализовать алгоритм, работающий в обратном направлении. Такой алгоритм называется алгоритмом обратного хода. Несмотря на некоторую сложность для человеческого восприятия, алгоритм обратного хода весьма активно используется в математике, и в ряде случаев его использование менее ресурсоемко, чем у алгоритма прямого хода. Основные принципы динамического программирования для алгоритма обратного хода остаются без изменения. Основным его отличием от алгоритма прямого хода заключается в том, что если последний начинает свою работу с пустого решения и добавляет ему по мере работы недостающие фрагменты, то алгоритм обратного хода начинает с предпосылки, что задача решена и, оперируя абстрактным полным решением, постепенно добавляет в него конкретные величины. В ряде случаев (например, в задаче поиска кратчайшего маршрута) его отличие от метода прямого хода весьма иллюзорно, в других – может существенно изменить ход решения. Рассмотрим задачу обратного хода на предыдущем примере.
350
