
Жолобов Ввведение в Математическое 2008
.pdf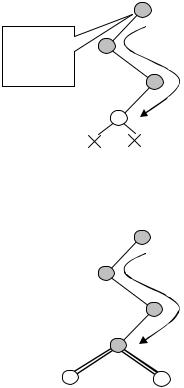
|
|
|
Вершина со |
|
|
всеми |
Расширение |
|
ветвями |
||
отбрасывает |
частичного |
|
ся |
||
решения |
||
|
Рис.2.30. Случай недопустимости задачи
Далее предпринимается попытка расширить оба новых реше-
ния.
Расширение
частичного
решения
Новые частичные решения
Рис.2.31. Случай ветвления
Очевидно, что нужно провести расширение сначала одного нового решения, а затем – другого. То есть необходимо создать список частичных решений.
3.Получено полное решение задачи, т.е., допустимое решение исходной задачи.
Возникает вопрос, как наиболее эффективно использовать по-
лученную информацию. Вот здесь-то и используется механизм, который уже рассматривался в методе Фора и Мальгранжа.
Этот механизм позволяет ускорить процесс отсеивания частичных решений, которые не только являются недопустимыми, но и, что самое интересное, заведомо неоптимальными.
331

Работа этого механизма будет рассмотрена несколько позже. Сейчас же приведем важнейшее в аддитивном алгоритме определение (уже знакомое из метода ветвей и границ).
Допустимое решение X * (x1* , x2* ,..., xn* ) , которое доставляет
ЦФ значение Z* – большее, чем любое известное к данному моменту решение, называется рекордом.
Рекорды мы будем регистрировать – запоминать только последний рекорд.
В принципе, можно каждое полное частичное решение сравнивать с рекордом: если рекорд не улучшился, отбрасывать это решение.
Мы же воспользуемся механизмом метода Фора и Мальгран-
жа.
После того, как получен очередной рекорд ( X * , Z* ), в систему ограничений каждой из задач, которая соответствует некоторому, еще не расширенному решению, будем добавлять ограничение:
n
cj xj F ( X * ) 1.
j 1
Таким образом, каждое полное расширенное решение будет соответствовать новому рекорду.
Ниже приводится общая схема аддитивного алгоритма.
Шаг 1. |
Положим |
= , v N (все переменные – свобод- |
ные). Придадим |
задаче стандартную форму и занесем ее в предва- |
|
рительно очищенный список задач. |
||
Шаг 2. |
Если список задач пуст, то проверяем, был ли ранее зафик- |
|
сирован рекорд. Если рекорд был зафиксирован, задача решена:
рекорд X * – оптимальное решение, Z* – оптимальное значение ЦФ. Конец.
Шаг 3. Если при пустом списке рекорд не зафиксирован, задача не имеет допустимых решений. Конец.
Шаг 4. Если список задач не пуст, выберем из него любую задачу. По признаку пустого подмножества ( bi 0 ) проверяем допустимость задачи, и, если признак есть, переходим к шагу 2. Если признака нет (все bi 0, i 1,m ), выполняется следующий шаг.
332
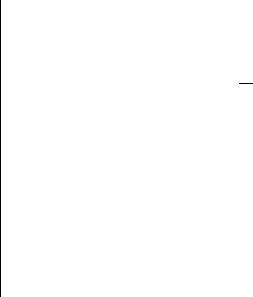
Шаг 5. Производим расширение частичного решения, которому соответствует выбранная задача. Если устанавливается факт недо-
пустимости задачи, соответствующей расширенному решению ( bi 0 ) переходим к шагу 2.
Шаг 6. Если расширенное частичное решение полное, то получен
новый рекорд ( X * , Z* ).
Во все задачи списка вносим дополнительное ограничение
n
cj xj F ( X * ) 1,
j 1
учитывая соответствующие частичные решения. Всем задачам списка придаем стандартную форму и переходим к шагу 2.
Шаг 7. Имеем неполное расширенное частичное решение. Возьмем любую свободную переменную этого решения xk (k v). Полагая xk=1 и xk=0 (v=v\k, = k) формируем два частичных решения. Каждому из этих частичных решений ставим в соответствие задачу в стандартной форме (естественно, с учетом дополнительного ограничения, если ранее был зафиксирован рекорд). Заносим эти задачи в список и переходим к шагу 2.
Пример 2.26
Используя аддитивный алгоритм, решить задачу ЛЦП(б): 10x1 2x2 3x3 14x4 max
4x1 5x2 10x3 4x4 11 9x1 4x2 3x3 5x4 5
x j {0,1}, j 1, 4.
Положим = , v={1,2,3,4} – все переменные частичного решения – свободные. Это решение имеет вид x1 , x2 , x3 , x4 .
Задача имеет вид основной задачи. Придадим ей стандартную форму.
10x1 2x2 3x3 14x4 max 4x '1 5x '2 10 x '3 4x4 8
9x1 4x2 3x3 5x '4 10
Занесем эту задачу в список (для упрощения записи спецификация переменных опущена).
Выберем задачу из списка. Ее частичное решение x1, x2 , x3 , x4 . Признака пустого подмножества нет. Начнем расширять частичное
333

решение.
x '3 0 x3 1 . Новое ЧР x1 , x2 ,1, x4 .
Новая задача:
10x1 2x2 14x4 3 max
4x '1 5x '2 |
4x4 8 |
9 x1 4x2 5x '4 7
x1 0 x '1 1 . Новое ЧР 0, x2 ,1, x4 .
Новая задача:
2x2 14x4 3 max
5 x '2 |
4x4 4 |
4x2 5x '4 7
x '2 0 x2 1 . Новое ЧР 0,1,1, x4 .
Новая задача:
14x4 5 max
4x4 4
5 x '4 3
x '4 0 x4 1 . Новое ЧР 0,1,1,1 полное. Получен рекорд.
X * =( 0,1,1,1 ), Z * =19.
Список задач пустой. Рекорд зафиксирован. Следовательно, имеем оптимальное решение ЛЦП(б)-задачи:
X opt =( 0,1,1,1 ), Zopt =19.
2.6.5.Моделирование логических высказываний
взадачах булева программирования
Логическое высказывание Tj , которое может быть либо ис-
тинным, либо ложным, можно моделировать бинарной (булевой) переменной x j :
1, если Tj истинно, xj 0, если Tj ложно.
Отрицание ( Tj ) моделируется, как (1- x j ). Промоделируем некоторые высказывания.
334
1. "T1 или T2 или ...или Tk истинно". В этом случае нужно сфор-
мулировать ограничение, которое "заставит" принять единичное значение по крайней мере одну переменную. Таким ограничением может служить следующее:
x1 x2 ... xk 1.
2. "T1 и T2 и ... и Tk истинно". Модель этого высказывания име-
ет вид:
x1 x2 ... xk k .
3. "Одно и только одно из высказываний T1 и T2 и ... и Tk истин-
но":
x1 x2 ... xk 1.
А теперь рассмотрим сложные высказывания.
4."Tk 1 истинно тогда и только тогда, когда все высказывания
T1 |
и T2 и ... и Tk истинны": Tk 1 |
T1 T2 |
... Tk . Это высказыва- |
|||||||
ние моделируется двумя ограничениями: |
|
|
|
|||||||
а) |
x1 x2 |
... xk kxk 1 – если хотя бы l |
высказываний ложны, то |
|||||||
k l kxk 1 , откуда следует, что xk 1 =0, |
|
|
|
|||||||
б) |
x1 x2 ... xk (k 1) xk 1 |
– если все высказывания истинны, |
||||||||
то k l kxk 1 , |
откуда следует, что xk 1 =1. |
|
|
|||||||
5. |
"Tk 1 истинно тогда и только тогда, когда хотя бы одно из вы- |
|||||||||
сказываний |
T1 |
и T2 и ... |
и Tk |
истинно": |
|
|
|
|||
|
Tk 1 T1 |
T2 |
... Tk . |
Это |
высказывание |
также |
моделируется |
|||
двумя ограничениями: |
|
|
|
|
|
|
||||
а) |
x1 x2 |
... xk kxk 1 – |
если хотя бы одно |
из |
высказываний |
|||||
истинно, |
то xk 1 =1; |
|
|
|
|
|
|
|||
б) |
x1 x2 ... xk xk 1 |
– если |
все высказывания |
ложны, то |
||||||
k l kxk 1 , откуда следует, что xk 1 =0.
Введенная таким образом формализация уже вполне достаточна, чтобы моделировать высказывания любой сложности.
335
Пример 2.27
Возьмем импликацию:
T3 T1 T2 .
( T3 ложно тогда и только тогда, когда T1 истинно, а T2 ложно). Эквивалентная запись этого высказывания имеет вид:
T3 T1 T2 .
Высказывание T3 T1 T2 моделируется как (1- x j ), а дизъ-
юнкция моделируется, как уже было показано в пп.5 – двумя ограничениями:
(1 x1 ) x2 2x3 ,
1 x1 x2 x3 .
Итак, возможность моделирования высказываний любой сложности открывает широкие перспективы для моделирования таких сложных ситуаций, ярким примером одной из которых является оптимизация планирования взаимоувязанного комплекса работ по созданию сложной системы.
Необходимо наладить выпуск продукции и обеспечить максимальную прибыль от ее реализации.
Сразу возникает масса альтернативных вариантов, где размещать производство и какую технологию использовать для выпуска продукции.
Для каждого альтернативного варианта возникает свой круг проблем:
Ресурсное обеспечение (материальные, трудовые, финансовые ресурсы). Здесь также возможны варианты.
Оптимальная кооперация (каких смежников привлекать, что оставлять смежникам, что производить самим).
Инфраструктура (сбыт продукции). Какие требуются коммуникации.
Экология, социальное развитие, капитальные вложения в непроизводственную сферу.
Возможность переориентации производства при насыщении рынка.
При решении подобных проблем вся плановая информация, при хорошей ее структуризации, развертывается в граф, вершинам
336
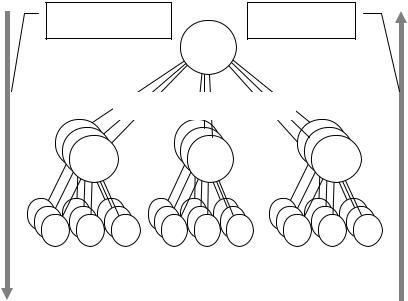
которого соответствуют работы по созданию отдельных подсистем
(рис. 2.32).
Основная логика этого графа – это "И/ИЛИ". Построение же графа идет сверху вниз.
Планирование Реализация
|
И |
|
или |
или |
или |
ИИИ |
ИИИ |
ИИИ |
Рис.2.32. Дерево целей
В процессе планирования этот граф последовательно (сверху вниз) преобразуется в граф, имеющий логику "И". То есть для каждой цели (подцели) выбирается свой вариант реализации из множества альтернативных вариантов.
Полученный таким образом граф преобразуется в исполнительный план, в план-график, для работы с которым используются методы сетевого планирования.
Вот здесь-то следует подчеркнуть одну важную особенность булева программирования.
Модели ЛЦП(б) позволяют учитывать взаимную обусловленность не только работ, относящихся к одному комплексу (работа такая-то не может быть выполнена до тех пор, пока не будет выполнены все работы, связанные с достижением целей нижнего уровня), но и работ, относящихся к разным комплексам.
337
Это как раз и выражается определенными логическими высказываниями, которые включаются в модель задачи в виде линейных ограничений с булевыми переменными.
Остановимся на основных типах высказываний, задающих взаимообусловленность плановых решений и на моделях этих высказываний – на вопросах моделирования логических связей.
2.6.6. Моделирование логических связей
взадачах булева программирования
Вкачестве объекта планирования возьмем самый общий объект – большую сложную систему, состоящую из ряда подсистем.
Пусть x j – булева переменная, значение которой определяет включение в план (исключение из плана) разработку некоторой
подсистемы Aj |
: |
|
|
|
|
|
|
|
|
|
1, |
разработка |
A |
j |
|
включается в план, |
|
xj |
|
|
|
|
|
|
|
|
|
0, |
разработка A |
|
не включается в план. |
||||
|
|
|
j |
|||||
|
|
|
|
|
|
|
|
|
То есть переменная x j |
моделирует атомарное высказыва- |
|||||||
ние Aj : "создать подсистему Aj ".
Информация, предоставляемая для разработки плана создания системы, помимо перечня вариантов проектов и их составляющих, содержит также сведения об их логических взаимосвязях. Приведем примеры моделирования типичных логических связей.
1. Создание любой системы из множества A1 , A2 ,..., Ak исключа-
ет создание других систем этого множества.
Это так называемое "альтернативное разбиение", которое соответствует высказыванию:
T1 T2 ... Tk .
Это высказывание ложно тогда и только тогда, когда истинными являются более одной пропозициональной переменной.
Высказывание моделируется следующим ограничением: x1 x2 ... xk 1.
338
2. Система Ai может быть создана только после того, как будет создана система A1 , A2 ,..., Ak .
Высказывание: Ti Tk . Модель этого высказывания:
xk xi .
3. Подсистему Ai можно начать разрабатывать только в том
случае, если будут разработаны все подсистемы множества
A1 , A2 ,..., Ak .
Высказывание: Ti Tk . Модель этого высказывания:
x1 x2 ... xk kxk 1 .
4. Подсистему Ai можно начать разрабатывать только в том
случае, если будет разработана по крайней мере одна из подсистем множества A1 , A2 ,..., Ak .
Высказывание: Ti Tk . Модель этого высказывания:
x1 x2 ... xk xk 1 .
В завершение этого раздела необходимо подчеркнуть следующее обстоятельство. Сложные предложения, включенные в информацию, представленную для разработки плана, всегда имеют значение "истинно".
Задача разработки плана является в определенном смысле обратной той задаче, которая решается с помощью таблиц истинности – по известным значениям пропозициональных переменных найти значения сложных логических выражений. В нашем же случае требуется найти значения пропозициональных переменных, обеспечивающие истинность логических выражений, включенных в математическую модель задачи в виде соответствующих ограничений.
339

Пример 2.28
На модернизацию АЭС, состоящей из трех энергоблоков, выделена сумма А.
Для каждого энергоблока i ( i 1, 2,3 ) подготовлено mi проектов модернизации: Pi1 , Pi 2 ,..., Pi mi , из которых может быть выбран только один вариант (а может, и ни одного).
Реализация проекта Pij требует затрат на сумму aij и дает до-
полнительный доход в сумме cij .
Построить модель задачи выбора проекта модернизации, обеспечивающего максимальный дополнительный доход при условии, что
проект P12 может быть реализован только после того, как будут реали-
зованы проекты P21 и P31 . Решение.
Вводим булевы переменные xij {0,1}, такие, что: |
|
||||||
xij |
1, |
если i й энергоблок модернизируетсяпо |
j му проекту |
||||
|
в противном случае. |
|
|||||
|
0, |
|
|||||
Моделируем дополнительное ограничение: |
|
||||||
x21 x31 |
2x12 . |
|
|
|
|
||
Окончательно: |
|
|
|
|
|||
3 |
mj |
|
|
|
|
|
|
cij xij |
max, |
|
|
|
|
||
i 1 |
j 1 |
|
|
|
|
|
|
3 |
mj |
|
|
|
|
|
|
aij |
xij |
A– ограничение на затраты на модернизацию. |
|||||
i 1 |
j 1 |
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
i |
xij 1 , |
i 1, 2,3, – не более одного варианта модернизации. |
|||||
j 1 |
|
|
|
|
|
|
|
x21 x31 |
2x12 , – модель дополнительного ограничения. |
||||||
xij |
|
|
|
|
|
|
|
{0,1), |
i 1, 2, 3; |
j 1, mi . |
|
||||
340
